What Fractions Are Equivalent To 5/10
Treneri
May 14, 2025 · 5 min read
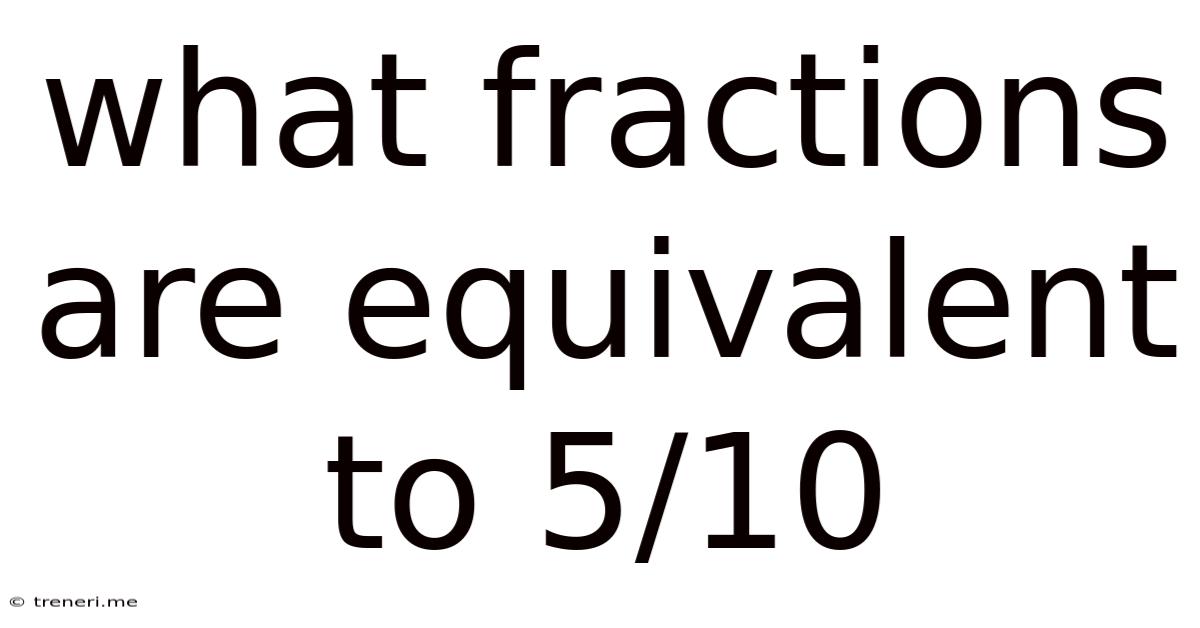
Table of Contents
What Fractions Are Equivalent to 5/10? A Deep Dive into Equivalent Fractions
Finding equivalent fractions is a fundamental concept in mathematics, crucial for understanding fractions, simplifying expressions, and solving various mathematical problems. This article delves into the intricacies of finding fractions equivalent to 5/10, exploring the underlying principles and providing a comprehensive understanding of this topic. We’ll go beyond simply identifying equivalent fractions and delve into the practical applications and theoretical implications of this concept.
Understanding Equivalent Fractions
Equivalent fractions represent the same value despite having different numerators and denominators. Think of it like this: cutting a pizza into 10 slices and taking 5 represents the same amount as cutting the same pizza into 2 slices and taking 1. Both represent half the pizza. The key to finding equivalent fractions lies in the concept of multiplying or dividing both the numerator and the denominator by the same non-zero number. This maintains the ratio and thus the value of the fraction.
The Core Principle: If you multiply or divide both the numerator and the denominator of a fraction by the same non-zero number, the resulting fraction will be equivalent to the original fraction.
Example: Consider the fraction 1/2. If we multiply both the numerator and denominator by 2, we get 2/4. Similarly, multiplying by 3 gives us 3/6, multiplying by 4 gives 4/8, and so on. All these fractions – 1/2, 2/4, 3/6, 4/8 – are equivalent. They all represent the same proportion or part of a whole.
Finding Fractions Equivalent to 5/10
Let's apply this principle to our target fraction, 5/10. We can find equivalent fractions by both simplifying (reducing) and expanding the fraction.
Simplifying 5/10: Finding the Simplest Form
The simplest form of a fraction is when the numerator and denominator have no common factors other than 1 (they are coprime). To simplify 5/10, we need to find the greatest common divisor (GCD) of 5 and 10. The GCD of 5 and 10 is 5. We then divide both the numerator and the denominator by the GCD:
5 ÷ 5 / 10 ÷ 5 = 1/2
Therefore, the simplest form of 5/10 is 1/2. This is the most reduced and commonly used equivalent fraction.
Expanding 5/10: Generating More Equivalent Fractions
To find more equivalent fractions, we can multiply both the numerator and the denominator by the same number. Let's try a few examples:
- Multiply by 2: (5 x 2) / (10 x 2) = 10/20
- Multiply by 3: (5 x 3) / (10 x 3) = 15/30
- Multiply by 4: (5 x 4) / (10 x 4) = 20/40
- Multiply by 5: (5 x 5) / (10 x 5) = 25/50
- Multiply by 6: (5 x 6) / (10 x 6) = 30/60
And so on. We can generate an infinite number of equivalent fractions by multiplying by any non-zero integer. All these fractions – 10/20, 15/30, 20/40, 25/50, 30/60, and countless others – are equivalent to 5/10.
Practical Applications of Equivalent Fractions
Understanding equivalent fractions is crucial in various real-world scenarios and mathematical applications:
-
Measurement Conversions: Converting units of measurement often involves working with equivalent fractions. For example, converting inches to feet or centimeters to meters requires understanding the proportional relationships between the units, which relies on the concept of equivalent fractions.
-
Baking and Cooking: Recipes often require adjusting ingredient quantities based on the number of servings. Equivalent fractions are used to scale recipes up or down, ensuring that the proportions of ingredients remain the same.
-
Geometry and Proportion: Solving geometric problems involving similar triangles or proportional relationships often involves finding equivalent fractions to determine unknown lengths or angles.
-
Data Analysis and Statistics: In statistics, equivalent fractions help in simplifying ratios and proportions in data analysis, making it easier to interpret results and draw conclusions.
-
Algebra and Equation Solving: Solving algebraic equations involving fractions often requires finding common denominators, which necessitates the understanding and application of equivalent fractions.
Beyond the Basics: Visualizing Equivalent Fractions
Visual representations can greatly enhance understanding. Imagine a rectangular bar representing a whole. If you divide it into 10 equal parts and shade 5, you represent 5/10. Now, imagine dividing the same bar into 2 equal parts and shading one. You've represented 1/2. Visually, both representations cover the same area, illustrating the equivalence.
The Importance of Simplifying Fractions
While you can have countless equivalent fractions, simplifying to the simplest form is often preferred for several reasons:
-
Clarity and Readability: Simpler fractions are easier to understand and interpret, making mathematical expressions less cumbersome.
-
Efficiency in Calculations: Calculations involving simpler fractions are generally faster and less prone to errors.
-
Comparison and Ordering: Comparing and ordering fractions is easier when they are in their simplest form.
Conclusion: Mastering Equivalent Fractions
Understanding equivalent fractions is a cornerstone of mathematical fluency. By mastering the principles of multiplying and dividing both the numerator and denominator by the same non-zero number, you can confidently simplify, expand, and manipulate fractions to solve various problems in mathematics and beyond. Remember that while countless fractions are equivalent to 5/10, the simplified form of 1/2 is often the most efficient and readily understood representation. The ability to effortlessly identify and work with equivalent fractions will greatly enhance your mathematical capabilities and open doors to more complex mathematical concepts. Regular practice and visual aids are highly recommended to solidify your understanding.
Latest Posts
Latest Posts
-
Cost Of Thinset Per Square Foot
May 14, 2025
-
What Is The Gcf Of 63 And 81
May 14, 2025
-
How Many Minutes Is 33 Hours
May 14, 2025
-
Greatest Common Factor Of 21 And 42
May 14, 2025
-
How Many Ounces Are In 2000 Ml
May 14, 2025
Related Post
Thank you for visiting our website which covers about What Fractions Are Equivalent To 5/10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.