What Fractions Are Equivalent To 8/12
Treneri
May 09, 2025 · 5 min read
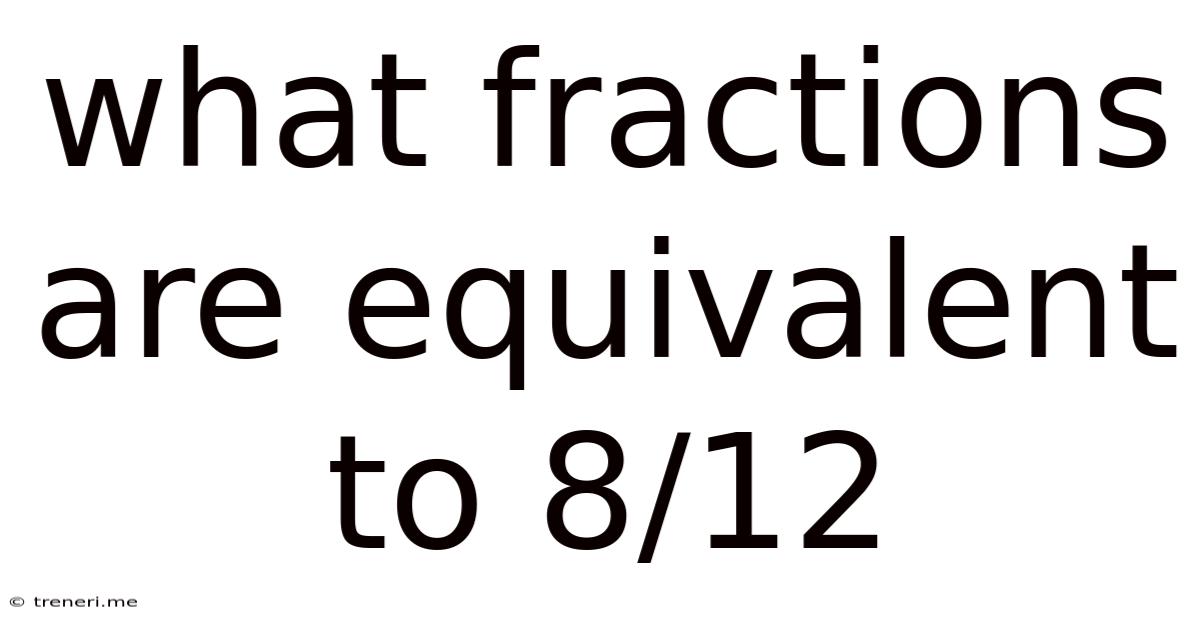
Table of Contents
What Fractions Are Equivalent to 8/12? A Comprehensive Guide
Finding equivalent fractions is a fundamental concept in mathematics, crucial for understanding ratios, proportions, and simplifying expressions. This comprehensive guide delves into the various methods for determining fractions equivalent to 8/12, exploring the underlying principles and providing practical examples to solidify your understanding. We'll also touch upon the importance of simplifying fractions to their lowest terms.
Understanding Equivalent Fractions
Equivalent fractions represent the same proportion or value, even though they appear different. Imagine slicing a pizza: 8/12 represents 8 slices out of a 12-slice pizza. If you cut the same pizza into smaller or larger pieces, you can still represent the same amount of pizza with different fractions. These different fractions are equivalent to 8/12.
The key principle behind equivalent fractions lies in the relationship between the numerator (top number) and the denominator (bottom number). You can create equivalent fractions by multiplying or dividing both the numerator and the denominator by the same non-zero number. This process maintains the proportion and thus the value of the fraction.
Methods for Finding Equivalent Fractions of 8/12
Several methods help you efficiently determine fractions equivalent to 8/12. Let's explore them:
1. Simplifying to the Lowest Terms (Reducing the Fraction)
This is arguably the most important method, as it provides the simplest representation of the fraction. To simplify a fraction, you find the greatest common divisor (GCD) or greatest common factor (GCF) of both the numerator and the denominator. The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
For 8/12:
- Factors of 8: 1, 2, 4, 8
- Factors of 12: 1, 2, 3, 4, 6, 12
The greatest common factor of 8 and 12 is 4. Divide both the numerator and denominator by 4:
8 ÷ 4 = 2 12 ÷ 4 = 3
Therefore, the simplest form of 8/12 is 2/3. This is the most fundamental equivalent fraction.
2. Multiplying the Numerator and Denominator by the Same Number
You can generate an infinite number of equivalent fractions by multiplying both the numerator and the denominator by any non-zero whole number. Let's try a few examples:
- Multiply by 2: (8 x 2) / (12 x 2) = 16/24
- Multiply by 3: (8 x 3) / (12 x 3) = 24/36
- Multiply by 4: (8 x 4) / (12 x 4) = 32/48
- Multiply by 5: (8 x 5) / (12 x 5) = 40/60
- Multiply by 10: (8 x 10) / (12 x 10) = 80/120
All these fractions – 16/24, 24/36, 32/48, 40/60, 80/120, and countless others – are equivalent to 8/12. They all represent the same proportion.
3. Using a Table to Organize Equivalent Fractions
Creating a table can be helpful, especially when dealing with multiple equivalent fractions. This systematic approach avoids errors and provides a clear visual representation:
| Numerator | Denominator | Simplified Fraction |
|---|---|---|
| 8 | 12 | 2/3 |
| 16 | 24 | 2/3 |
| 24 | 36 | 2/3 |
| 32 | 48 | 2/3 |
| 40 | 60 | 2/3 |
| 48 | 72 | 2/3 |
| ... | ... | 2/3 |
This table clearly demonstrates that all these fractions, despite their different numerators and denominators, simplify to the same value: 2/3.
Why Simplifying Fractions is Important
Simplifying fractions to their lowest terms is crucial for several reasons:
-
Clarity and Simplicity: Simplified fractions are easier to understand and work with. 2/3 is far simpler to grasp than 40/60, even though they represent the same value.
-
Efficiency in Calculations: Using simplified fractions reduces computational complexity, especially when performing addition, subtraction, multiplication, or division of fractions.
-
Standardized Representation: Simplifying fractions ensures a consistent and unambiguous representation of a given proportion.
-
Better Understanding of Ratios and Proportions: Simplified fractions provide a clearer understanding of the underlying ratio.
Real-World Applications of Equivalent Fractions
The concept of equivalent fractions is far from abstract; it has numerous practical applications in daily life:
-
Cooking and Baking: Recipes often require adjusting ingredient amounts. Equivalent fractions are essential for accurately scaling recipes up or down.
-
Measurement and Construction: Converting between different units of measurement (e.g., inches to feet, centimeters to meters) often involves using equivalent fractions.
-
Financial Calculations: Understanding percentages and proportions in finance relies heavily on the concept of equivalent fractions.
-
Data Analysis and Statistics: Representing data visually using charts and graphs often requires simplifying fractions to convey information effectively.
Advanced Concepts Related to Equivalent Fractions
While we've focused on the basics, let's briefly touch upon some advanced concepts related to equivalent fractions:
-
Rational Numbers: Equivalent fractions form the basis of understanding rational numbers, which are numbers that can be expressed as a ratio of two integers (a fraction).
-
Proportionality: Equivalent fractions are the foundation of proportionality, which is a crucial concept in algebra and many scientific fields.
-
Ratio and Proportion Problems: Many real-world problems involving ratios and proportions can be solved using the principles of equivalent fractions.
-
Decimal Representation: Every fraction has an equivalent decimal representation, and understanding this relationship helps in converting between fractions and decimals.
Conclusion
Understanding equivalent fractions is a fundamental skill with wide-ranging applications. By mastering the methods outlined above—simplifying to lowest terms and multiplying the numerator and denominator by the same number—you can confidently work with fractions and solve problems involving ratios and proportions. Remember, the core principle remains the same: maintaining the proportion between the numerator and the denominator. Practicing these methods will solidify your understanding and equip you with essential mathematical skills for various contexts. From baking a cake to understanding financial reports, equivalent fractions are a powerful tool in everyday life.
Latest Posts
Latest Posts
-
120 Days From April 15 2024
May 11, 2025
-
Can You Get Tan With A Uv Of 4
May 11, 2025
-
What Is 20 Percent Of 185
May 11, 2025
-
29 Acres Is How Many Square Feet
May 11, 2025
-
30 Is 20 Percent Of What Number
May 11, 2025
Related Post
Thank you for visiting our website which covers about What Fractions Are Equivalent To 8/12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.