What Fractions Are Equivalent To 9 12
Treneri
May 11, 2025 · 5 min read
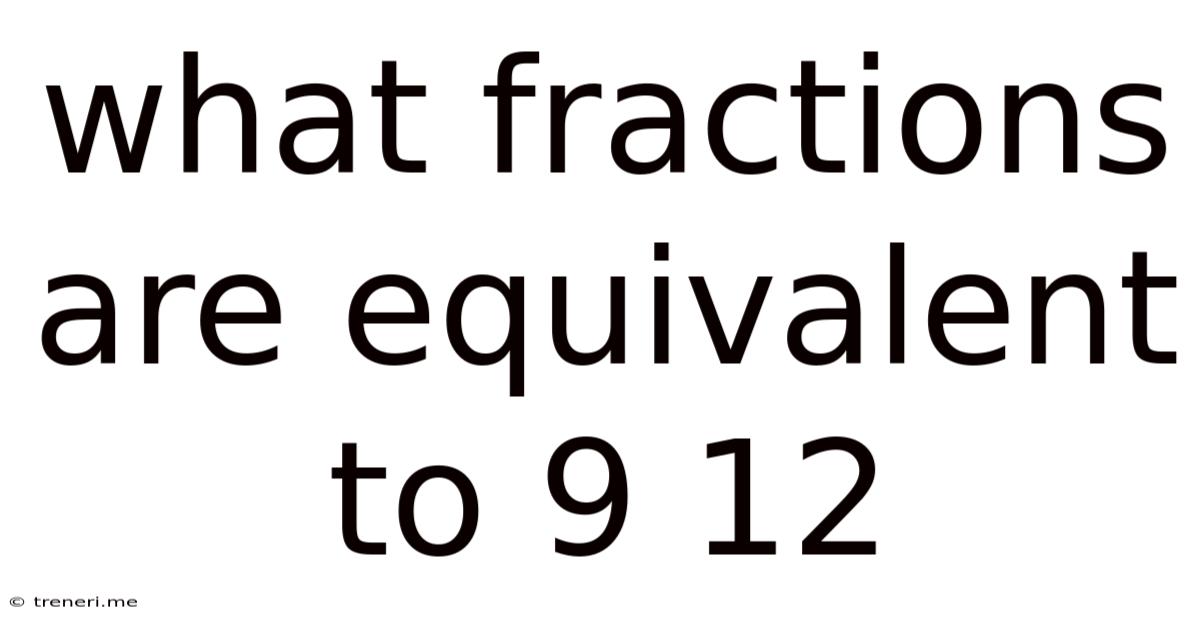
Table of Contents
What Fractions Are Equivalent to 9/12? A Comprehensive Guide
Finding equivalent fractions is a fundamental concept in mathematics, crucial for simplifying expressions, comparing values, and solving a wide range of problems. This guide will delve into the process of determining fractions equivalent to 9/12, exploring the underlying principles, providing numerous examples, and highlighting practical applications. We'll also touch upon the broader concept of simplifying fractions to their lowest terms.
Understanding Equivalent Fractions
Equivalent fractions represent the same proportion or part of a whole, even though they look different. Think of slicing a pizza: You could have a pizza cut into 12 slices and eat 9, or you could have a smaller pizza cut into 4 slices and eat 3. In both cases, you've eaten ¾ of the pizza. These fractions, 9/12 and 3/4, are equivalent.
The key principle behind equivalent fractions is that you can multiply or divide both the numerator (top number) and the denominator (bottom number) by the same non-zero number without changing the fraction's value. This is because you're essentially multiplying or dividing by 1 (e.g., 2/2 = 1, 5/5 = 1).
Finding Equivalent Fractions for 9/12
Let's find some equivalent fractions for 9/12. We can do this by applying the principle of multiplying or dividing both the numerator and denominator by the same number.
Multiplying to Find Equivalent Fractions
Let's start by multiplying both the numerator and the denominator by different whole numbers:
- Multiply by 2: (9 x 2) / (12 x 2) = 18/24
- Multiply by 3: (9 x 3) / (12 x 3) = 27/36
- Multiply by 4: (9 x 4) / (12 x 4) = 36/48
- Multiply by 5: (9 x 5) / (12 x 5) = 45/60
- Multiply by 10: (9 x 10) / (12 x 10) = 90/120
As you can see, we can generate an infinite number of equivalent fractions by multiplying both the numerator and denominator by any non-zero whole number.
Dividing to Find Equivalent Fractions (Simplifying Fractions)
Dividing both the numerator and the denominator by the same number simplifies the fraction. This process helps to find the simplest form of a fraction, also known as reducing the fraction to its lowest terms. The greatest common divisor (GCD) plays a crucial role here.
The GCD of 9 and 12 is 3. This means that 3 is the largest number that divides both 9 and 12 without leaving a remainder. Therefore, we can simplify 9/12 by dividing both the numerator and the denominator by 3:
(9 ÷ 3) / (12 ÷ 3) = 3/4
This is the simplest form of the fraction 9/12. It's important to note that 3/4 is also equivalent to 9/12, 18/24, 27/36, and all the other fractions we generated by multiplying. All these fractions represent the same proportion – three-quarters.
Finding the Simplest Form: A Step-by-Step Process
To find the simplest form of any fraction, follow these steps:
-
Find the GCD: Identify the greatest common divisor (GCD) of the numerator and the denominator. You can do this using various methods, such as prime factorization or the Euclidean algorithm.
-
Divide by the GCD: Divide both the numerator and the denominator by the GCD. The resulting fraction will be in its simplest form.
Example: Let's find the simplest form of 36/48.
-
Find the GCD: The GCD of 36 and 48 is 12.
-
Divide by the GCD: (36 ÷ 12) / (48 ÷ 12) = 3/4
Therefore, the simplest form of 36/48 is 3/4. This confirms that 36/48 is equivalent to 9/12 and 3/4.
Practical Applications of Equivalent Fractions
Understanding equivalent fractions has numerous practical applications across various fields:
-
Baking and Cooking: Recipes often require adjustments based on the number of servings. Equivalent fractions are essential for scaling recipes up or down. For example, if a recipe calls for 3/4 cup of flour and you want to double the recipe, you'll need 6/8 cups (which simplifies to 3/4).
-
Construction and Engineering: Precise measurements are critical in construction and engineering projects. Equivalent fractions are used to convert between different units of measurement and ensure accuracy.
-
Finance and Accounting: Calculating proportions and percentages often involves using equivalent fractions. For instance, determining the fraction of a budget spent on a particular item.
-
Data Analysis: Equivalent fractions are vital when dealing with ratios, proportions, and percentages in data analysis and statistics.
-
Everyday Life: Numerous everyday scenarios involve fractions. Sharing items, calculating discounts, or understanding proportions in various contexts all rely on the fundamental concept of equivalent fractions.
Beyond the Basics: More on GCD and Fraction Simplification
Finding the greatest common divisor (GCD) is crucial for simplifying fractions. Here are two common methods:
1. Prime Factorization:
- Find the prime factorization of both the numerator and denominator.
- Identify the common prime factors.
- The GCD is the product of these common prime factors raised to the lowest power.
Example: Find the GCD of 36 and 48.
- Prime factorization of 36: 2² x 3²
- Prime factorization of 48: 2⁴ x 3
- Common prime factors: 2 and 3
- GCD: 2² x 3 = 12
2. Euclidean Algorithm:
The Euclidean algorithm is a more efficient method for finding the GCD, especially for larger numbers. It's based on repeated division with remainder:
- Divide the larger number by the smaller number and find the remainder.
- Replace the larger number with the smaller number, and the smaller number with the remainder.
- Repeat steps 1 and 2 until the remainder is 0.
- The last non-zero remainder is the GCD.
Example: Find the GCD of 36 and 48 using the Euclidean algorithm.
- 48 ÷ 36 = 1 with a remainder of 12.
- 36 ÷ 12 = 3 with a remainder of 0.
- The GCD is 12.
Mastering these methods will significantly improve your ability to simplify fractions quickly and efficiently.
Conclusion
Understanding equivalent fractions and simplifying fractions to their lowest terms is a crucial skill with wide-ranging applications. By grasping the fundamental principles, learning efficient methods for finding the GCD, and practicing regularly, you'll develop a strong foundation in this essential mathematical concept. Remember, the key lies in the consistent application of multiplying or dividing both the numerator and denominator by the same non-zero number. This simple yet powerful technique unlocks the ability to manipulate and interpret fractions effectively across diverse contexts.
Latest Posts
Latest Posts
-
Greatest Common Factor Of 8 And 28
May 11, 2025
-
Cuanto Falta Para El 1 De Septiembre 2024
May 11, 2025
-
15 X 30 Pool How Many Gallons Of Water
May 11, 2025
-
5 X 10 To The Power Of 4
May 11, 2025
-
How To Find Initial Horizontal Velocity
May 11, 2025
Related Post
Thank you for visiting our website which covers about What Fractions Are Equivalent To 9 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.