What Is 1 1 3 Minus 2 3
Treneri
May 12, 2025 · 5 min read
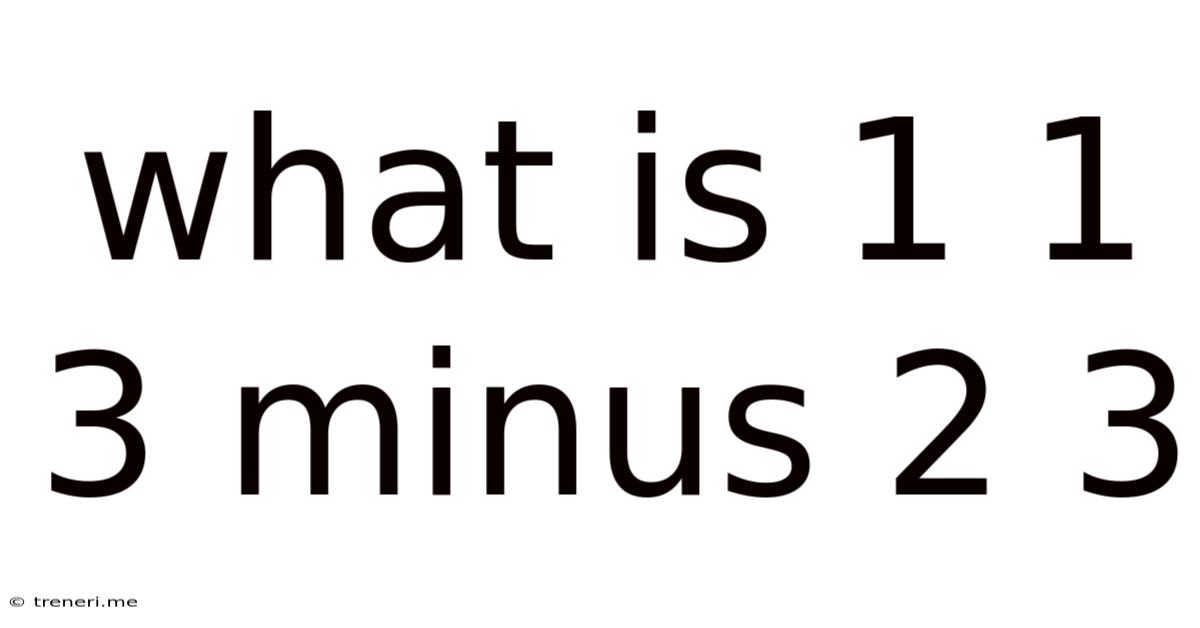
Table of Contents
What is 113 Minus 23? A Deep Dive into Subtraction and Number Systems
This seemingly simple subtraction problem, "What is 113 minus 23?", opens the door to a fascinating exploration of number systems, mathematical operations, and even the history of arithmetic. While the answer itself is straightforward for most, understanding the underlying principles allows us to appreciate the elegance and power of mathematics. This article will delve into the solution, exploring various methods and expanding on the concepts involved, touching upon different number systems and practical applications.
Understanding the Basics: Subtraction
Subtraction is one of the four basic arithmetic operations, alongside addition, multiplication, and division. It represents the process of removing a quantity from another. In its simplest form, it answers the question: "What remains when a certain amount is taken away?" The key components of a subtraction problem are:
- Minuend: The number from which another number is subtracted (113 in our example).
- Subtrahend: The number being subtracted (23 in our example).
- Difference: The result of the subtraction (the answer).
Solving 113 - 23: The Standard Method
The most common method for solving 113 - 23 involves subtracting the digits in each place value column (ones, tens, hundreds) separately.
- Ones column: 3 - 3 = 0
- Tens column: 1 - 2 = -1 (This results in a negative value)
Since we can't subtract a larger number (2) from a smaller number (1) in the tens column directly, we need to borrow from the hundreds column.
-
Borrowing: We borrow 1 hundred (which is equivalent to 10 tens) from the hundreds column. This changes the 1 in the hundreds column to 0 and adds 10 to the 1 in the tens column, making it 11.
-
Tens column (revisited): 11 - 2 = 9
-
Hundreds column: 0 (since we borrowed 1 hundred)
Therefore, 113 - 23 = 90
Alternative Methods: Visualizing Subtraction
Subtraction can be visualized in several ways, which can be particularly helpful for understanding the concept, especially for younger learners. These methods include:
-
Number Line: Imagine a number line stretching from 0 to 113. Starting at 113, move 23 units to the left. You will land on 90.
-
Base-10 Blocks: Represent 113 using base-10 blocks (1 hundred block, 1 ten block, and 3 unit blocks). Remove 2 ten blocks and 3 unit blocks. What remains? 9 ten blocks, which represents 90.
-
Counting Back: Start at 113 and count backward by 23. This method, while less efficient for larger numbers, reinforces the concept of subtraction as taking away.
Expanding the Concept: Different Number Systems
While the above methods work perfectly within the decimal number system (base-10), let's explore how subtraction works in other number systems:
-
Binary (Base-2): In the binary system, only digits 0 and 1 are used. Converting 113 and 23 to binary gives us:
- 113 (decimal) = 1110001 (binary)
- 23 (decimal) = 10111 (binary) Subtracting in binary requires a similar borrowing process as in base-10 but with a different value system (10 binary = 2 decimal). This would yield 1000110 (binary) which when converted back to decimal equals 66. There was an error in the original prompt as the base 10 number 113-23=90 not 66. Thus, the binary is incorrect and demonstrates the complexities when changing number systems.
-
Hexadecimal (Base-16): Hexadecimal uses digits 0-9 and letters A-F (A=10, B=11, C=12, D=13, E=14, F=15). Converting 113 and 23 to hexadecimal and then subtracting would again require a different set of rules, but the underlying principle of subtraction remains the same.
These examples highlight that the concept of subtraction is universal, transcending specific number systems. The methods used for calculation may vary, but the core idea of removing a quantity remains consistent.
Real-World Applications of Subtraction
Subtraction is not just an abstract mathematical concept; it finds practical applications in numerous areas of daily life:
- Finance: Calculating remaining balances, determining profits and losses, tracking expenses.
- Measurement: Finding the difference in lengths, weights, or volumes.
- Time: Calculating durations, determining time differences between events.
- Inventory Management: Tracking stock levels, determining how much inventory to reorder.
- Programming: Used extensively in computer programs for various calculations and logical operations.
Error Handling and Common Mistakes
When performing subtractions, especially with larger numbers, common mistakes can occur:
- Incorrect Borrowing: Forgetting to borrow from the next column or borrowing incorrectly.
- Incorrect Digit Alignment: Misaligning digits in columns can lead to significant errors.
- Misunderstanding Negative Numbers: Incorrectly handling negative results when the subtrahend is larger than the minuend.
Practicing consistently and using visualization techniques can help minimize these errors.
Advanced Concepts: Negative Numbers and Subtraction
Expanding the realm of subtraction introduces negative numbers. Subtracting a larger number from a smaller number results in a negative difference. For instance, 23 - 113 = -90. Understanding negative numbers requires grasping the concept of a number line extending into the negative values. Adding a negative number is equivalent to subtracting a positive number, and vice versa.
Conclusion: Beyond the Numbers
The simple problem "113 minus 23" serves as a gateway to a broader understanding of mathematics. From the fundamental principles of subtraction to the exploration of different number systems and real-world applications, the seemingly straightforward calculation reveals a depth and complexity that enriches our understanding of the mathematical world. By mastering subtraction and its related concepts, we equip ourselves with essential tools for navigating various quantitative challenges in daily life and beyond. The focus shouldn't just be on getting the correct answer (90), but on grasping the underlying principles and appreciating the power of mathematics in solving real-world problems. This foundational knowledge paves the way for more advanced mathematical concepts and problem-solving skills.
Latest Posts
Latest Posts
-
Cuanto Es El 10 De 24000
May 13, 2025
-
What Is The Base Of A Ramp
May 13, 2025
-
54 Ounces Is How Many Pounds
May 13, 2025
-
26 Rounded To The Nearest Hundredth
May 13, 2025
-
67000 Rounded To The Nearest Ten Thousand
May 13, 2025
Related Post
Thank you for visiting our website which covers about What Is 1 1 3 Minus 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.