What Is 1/4 Divided By 1 1/2 As A Fraction
Treneri
May 15, 2025 · 4 min read
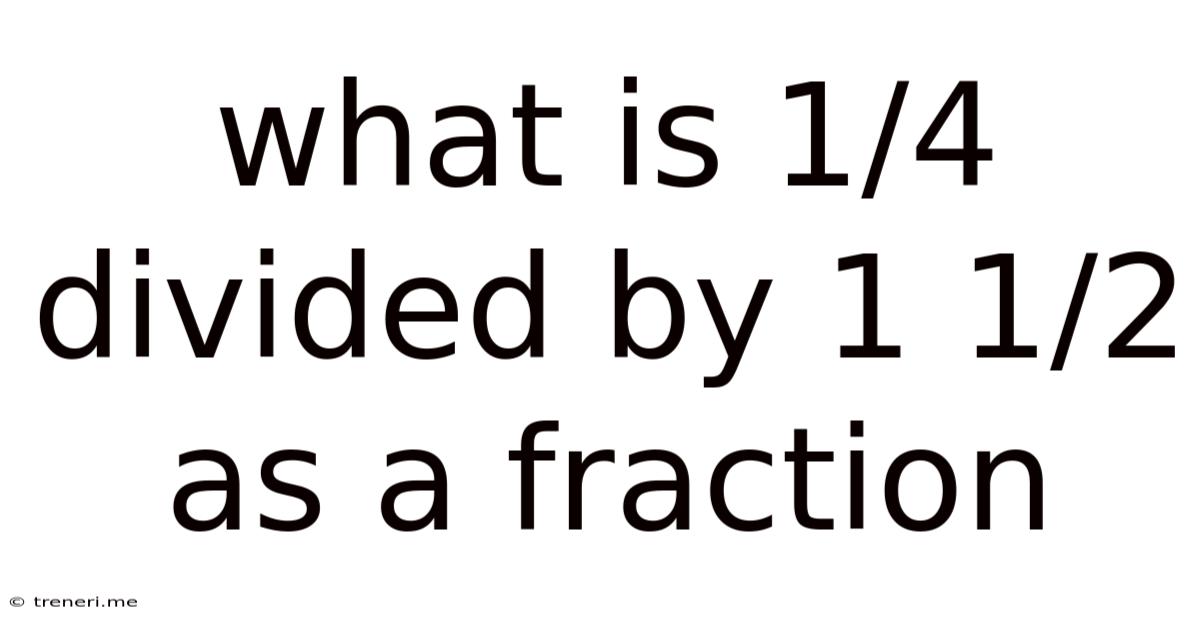
Table of Contents
What is 1/4 Divided by 1 1/2 as a Fraction? A Comprehensive Guide
Understanding fraction division can be tricky, but it's a fundamental skill in mathematics with applications across various fields. This comprehensive guide will walk you through the process of dividing fractions, specifically addressing the problem: What is 1/4 divided by 1 1/2 as a fraction? We'll cover the steps, provide helpful tips, and explore the underlying concepts to ensure you master this essential mathematical operation.
Understanding Fraction Division
Before tackling our specific problem, let's review the basics of dividing fractions. The key concept is to understand that dividing by a fraction is the same as multiplying by its reciprocal. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 2/3 is 3/2.
Here's the general rule for dividing fractions:
a/b ÷ c/d = a/b × d/c
Where 'a', 'b', 'c', and 'd' represent numbers, and 'b' and 'c' are not zero (division by zero is undefined).
This rule means we can convert a division problem into a multiplication problem, making it significantly easier to solve.
Solving 1/4 Divided by 1 1/2
Now, let's apply this knowledge to our specific problem: 1/4 ÷ 1 1/2.
First, we need to convert the mixed number 1 1/2 into an improper fraction. A mixed number combines a whole number and a fraction. To convert it to an improper fraction, we multiply the whole number by the denominator and add the numerator, keeping the same denominator.
1 1/2 = (1 × 2 + 1) / 2 = 3/2
Now our problem becomes:
1/4 ÷ 3/2
Next, we apply our rule for dividing fractions: We change the division to multiplication by using the reciprocal of the second fraction (3/2). The reciprocal of 3/2 is 2/3.
1/4 ÷ 3/2 = 1/4 × 2/3
Now, we simply multiply the numerators together and the denominators together:
(1 × 2) / (4 × 3) = 2/12
Finally, we simplify the resulting fraction by finding the greatest common divisor (GCD) of the numerator and the denominator. The GCD of 2 and 12 is 2. We divide both the numerator and denominator by the GCD:
2/12 = (2 ÷ 2) / (12 ÷ 2) = 1/6
Therefore, 1/4 divided by 1 1/2 is 1/6.
Step-by-Step Breakdown:
To reinforce the process, let's break down the solution step-by-step:
- Convert Mixed Number to Improper Fraction: Transform 1 1/2 into an improper fraction: 3/2.
- Rewrite the Problem: The problem now becomes 1/4 ÷ 3/2.
- Invert and Multiply: Invert the second fraction (3/2) to get its reciprocal (2/3) and change the division sign to a multiplication sign: 1/4 × 2/3.
- Multiply Numerators and Denominators: Multiply the numerators (1 × 2 = 2) and the denominators (4 × 3 = 12): 2/12.
- Simplify the Fraction: Simplify 2/12 by dividing both the numerator and the denominator by their greatest common divisor (GCD), which is 2: 1/6.
Visualizing Fraction Division
Visualizing the problem can help solidify understanding. Imagine you have 1/4 of a pizza. You want to divide this 1/4 slice into portions that are 1 1/2 (or 3/2) slices each. How many of these larger portions can you get from your smaller 1/4 slice? The answer, as we calculated, is 1/6. You can get 1/6 of a portion of the larger 1 1/2 slices.
Practical Applications of Fraction Division
Understanding fraction division is crucial in various real-world situations:
- Cooking and Baking: Scaling recipes up or down requires dividing fractions.
- Sewing and Crafts: Calculating fabric amounts or dividing materials.
- Construction and Engineering: Dividing measurements accurately for precise work.
- Data Analysis: Working with proportions and percentages in datasets.
Mastering fraction division improves your problem-solving skills and opens up the possibility of tackling more complex mathematical concepts with confidence.
Common Mistakes to Avoid
Several common mistakes can arise when dividing fractions:
- Forgetting to find the reciprocal: Remember to flip the second fraction before multiplying.
- Incorrectly converting mixed numbers: Ensure you accurately convert mixed numbers to improper fractions before performing the calculation.
- Simplifying errors: Always simplify the resulting fraction to its lowest terms.
Practice Problems
To solidify your understanding, try these practice problems:
- 2/5 ÷ 1/3
- 3/4 ÷ 2 1/2
- 1 1/3 ÷ 2/5
- 5/8 ÷ 1/4
- 2 1/4 ÷ 3/8
Remember to follow the steps outlined above: convert mixed numbers to improper fractions, find the reciprocal of the second fraction, multiply, and simplify.
Conclusion
Dividing fractions might seem daunting at first, but with practice and a clear understanding of the process, it becomes straightforward. By mastering this skill, you enhance your mathematical abilities and equip yourself to handle a wider range of problems in various contexts. Remember the key: invert and multiply! This simple rule unlocks the solution to even the most complex fraction division problems. Consistent practice will build your confidence and proficiency in this essential mathematical operation. So keep practicing, and you'll soon be a fraction division expert!
Latest Posts
Latest Posts
-
Cuanto Es 2 Metros En Inches
May 15, 2025
-
How Many More Hours Till 7 Am
May 15, 2025
-
How Long Is 127 Minutes In Hours
May 15, 2025
-
How Much Is 1 5 Cups In Oz
May 15, 2025
-
Least Common Denominator Of 4 And 9
May 15, 2025
Related Post
Thank you for visiting our website which covers about What Is 1/4 Divided By 1 1/2 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.