What Is 16 To The Power Of 2
Treneri
May 12, 2025 · 5 min read
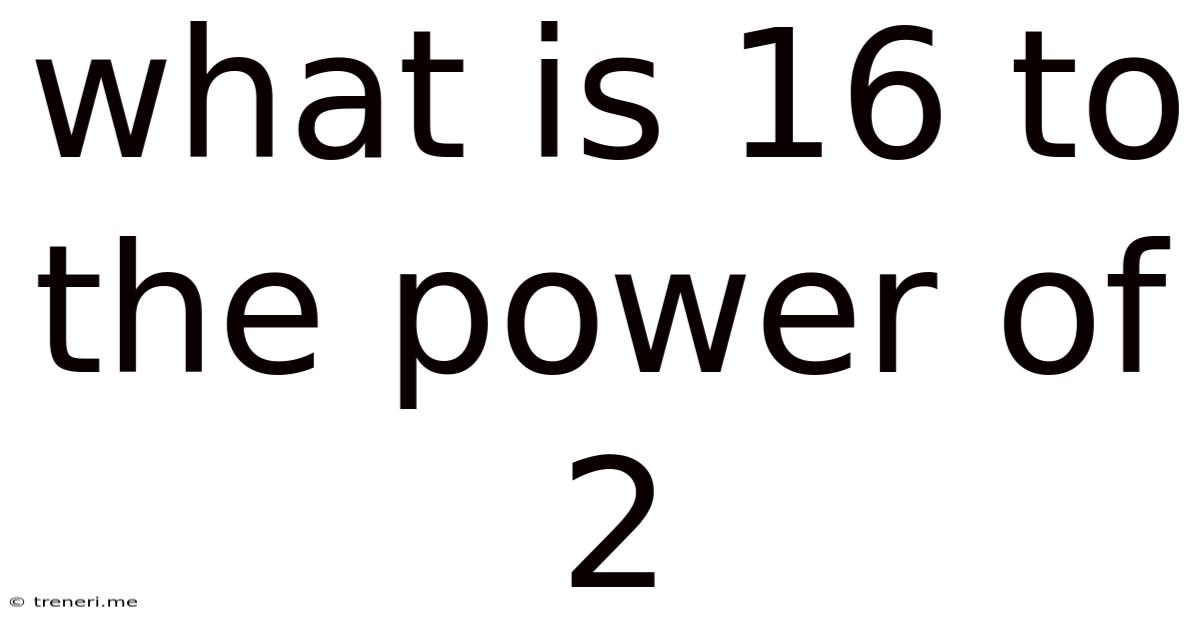
Table of Contents
What is 16 to the Power of 2? A Deep Dive into Exponents and Their Applications
Calculating 16 to the power of 2, or 16², might seem like a simple arithmetic problem. However, understanding this seemingly basic calculation opens the door to a broader understanding of exponents, their properties, and their widespread applications across various fields. This comprehensive guide will explore not only the answer to 16², but also the underlying principles, practical examples, and advanced concepts related to exponents.
Understanding Exponents: The Fundamentals
Before delving into the specifics of 16², let's establish a strong foundation in the concept of exponents. An exponent, also known as a power or index, indicates how many times a number (the base) is multiplied by itself. In the expression b<sup>n</sup>, b represents the base and n represents the exponent. Therefore, b<sup>n</sup> means b multiplied by itself n times.
For instance:
- 2³ = 2 × 2 × 2 = 8 (2 is the base, 3 is the exponent)
- 5² = 5 × 5 = 25 (5 is the base, 2 is the exponent)
- 10¹ = 10 (10 is the base, 1 is the exponent; any number raised to the power of 1 is itself)
- 7⁰ = 1 (Any non-zero number raised to the power of 0 is 1)
Calculating 16 to the Power of 2 (16²)
Now, let's address the central question: What is 16²? This simply means 16 multiplied by itself:
16² = 16 × 16 = 256
Therefore, 16 to the power of 2 is 256. This is a relatively straightforward calculation, especially with readily available calculators. However, the significance of this calculation extends beyond the simple arithmetic.
Exploring the Properties of Exponents
Understanding the properties of exponents is crucial for efficiently manipulating and solving problems involving exponential expressions. Here are some key properties:
-
Product of Powers: When multiplying two numbers with the same base, add the exponents: b<sup>m</sup> × b<sup>n</sup> = b<sup>(m+n)</sup>. For example, 2³ × 2² = 2<sup>(3+2)</sup> = 2⁵ = 32.
-
Quotient of Powers: When dividing two numbers with the same base, subtract the exponents: b<sup>m</sup> / b<sup>n</sup> = b<sup>(m-n)</sup>. For example, 2⁵ / 2² = 2<sup>(5-2)</sup> = 2³ = 8.
-
Power of a Power: When raising a power to another power, multiply the exponents: (b<sup>m</sup>)<sup>n</sup> = b<sup>(m×n)</sup>. For example, (2²)³ = 2<sup>(2×3)</sup> = 2⁶ = 64.
-
Power of a Product: When raising a product to a power, raise each factor to that power: (a × b)<sup>n</sup> = a<sup>n</sup> × b<sup>n</sup>. For example, (2 × 3)² = 2² × 3² = 4 × 9 = 36.
-
Power of a Quotient: When raising a quotient to a power, raise both the numerator and denominator to that power: (a / b)<sup>n</sup> = a<sup>n</sup> / b<sup>n</sup>. For example, (2/3)² = 2²/3² = 4/9.
Real-World Applications of Exponents
Exponents are not just abstract mathematical concepts; they have significant practical applications across numerous fields:
-
Science: Exponential growth and decay are fundamental concepts in various scientific disciplines. Population growth, radioactive decay, and compound interest all follow exponential patterns.
-
Finance: Compound interest calculations rely heavily on exponents. Understanding exponents is crucial for comprehending the power of compounding and making informed financial decisions.
-
Computer Science: Binary numbers, the foundation of digital computing, utilize exponents of 2. Understanding exponents is essential for working with computer memory, data storage, and algorithms.
-
Engineering: Exponents are frequently used in engineering calculations related to areas like structural design, fluid dynamics, and electrical circuits.
-
Physics: Many physical phenomena, including wave motion, energy calculations, and nuclear reactions, involve exponential functions.
Beyond 16²: Exploring Higher Powers and Negative Exponents
While 16² provides a simple example, the concept of exponents extends to much larger numbers and includes negative exponents.
-
Higher Powers: Calculating 16³ (16 to the power of 3) involves multiplying 16 by itself three times: 16 × 16 × 16 = 4096. Similarly, higher powers can be calculated using the same principle.
-
Negative Exponents: A negative exponent indicates the reciprocal of the base raised to the positive exponent. For example:
- 16⁻¹ = 1/16
- 16⁻² = 1/16² = 1/256
Scientific Notation and Exponents
Scientific notation uses exponents to represent very large or very small numbers concisely. A number in scientific notation is expressed as a × 10<sup>b</sup>, where a is a number between 1 and 10, and b is an integer exponent. This notation is commonly used in science and engineering to handle numbers with many digits.
Exponential Functions and Their Graphs
Exponential functions are functions of the form f(x) = a<sup>x</sup>, where a is a positive constant and x is the exponent. These functions exhibit characteristic exponential growth or decay depending on the value of a. Graphing exponential functions reveals their distinctive curves, illustrating the rapid increase or decrease associated with exponential growth or decay.
Solving Exponential Equations
Solving exponential equations involves finding the value of the unknown exponent. Techniques for solving exponential equations often involve using logarithms, which are inverse functions of exponents. Logarithms provide a way to isolate the exponent and solve for its value.
Conclusion: The Expanding World of Exponents
While the calculation of 16² might seem trivial at first glance, it serves as a gateway to understanding the broader world of exponents. From fundamental arithmetic operations to advanced mathematical concepts and real-world applications, exponents play a crucial role in various fields. This comprehensive exploration has touched upon the basics of exponents, their properties, practical examples, and advanced applications, emphasizing the pervasive and crucial role of exponents in our understanding of the world around us. Mastering exponents is not just about knowing the answer to 16²; it's about unlocking a deeper comprehension of mathematical principles and their far-reaching implications.
Latest Posts
Latest Posts
-
Gestation Period For Sheep In Months
May 14, 2025
-
9 30 To 3 30 Is How Many Hours
May 14, 2025
-
What Is The Greatest Common Factor Of 52 And 26
May 14, 2025
-
What Percent Is 24 Out Of 25
May 14, 2025
-
What Is The Greatest Common Factor Of 6 And 14
May 14, 2025
Related Post
Thank you for visiting our website which covers about What Is 16 To The Power Of 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.