What Is 18 Out Of 30 As A Percentage
Treneri
May 10, 2025 · 4 min read
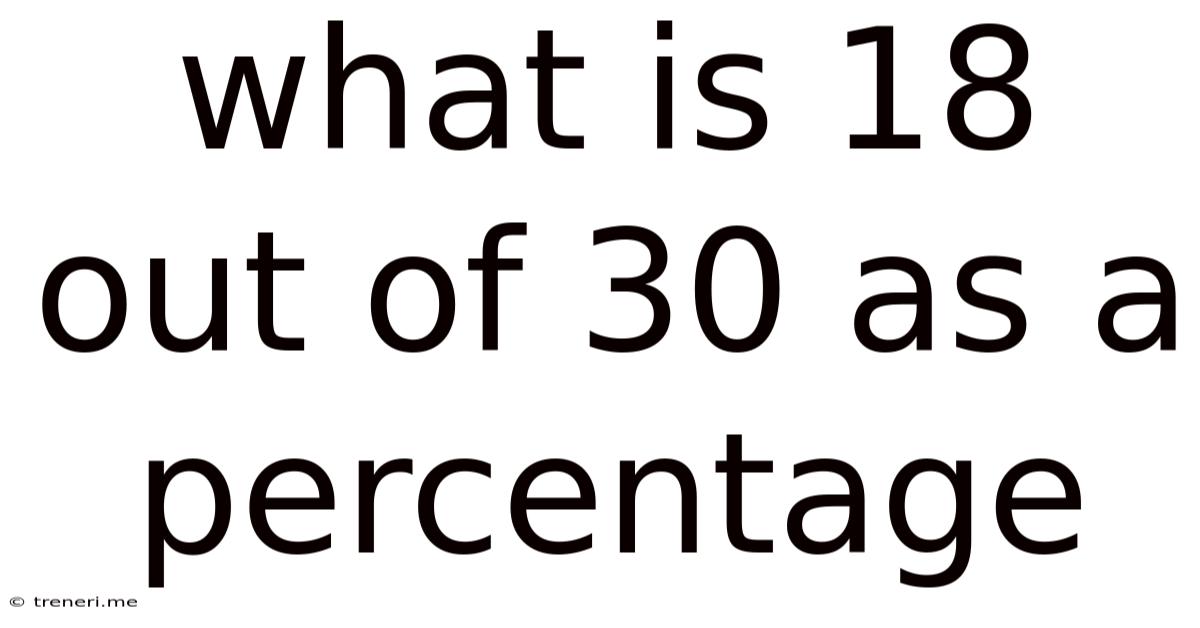
Table of Contents
What is 18 out of 30 as a Percentage? A Comprehensive Guide
Calculating percentages is a fundamental skill in many areas of life, from everyday finances to advanced statistical analysis. Understanding how to convert fractions to percentages is crucial for interpreting data, making informed decisions, and excelling in various academic and professional settings. This comprehensive guide will walk you through the process of determining what 18 out of 30 represents as a percentage, explaining the underlying concepts and providing practical applications. We'll explore multiple methods, ensuring you gain a solid grasp of this essential mathematical skill.
Understanding Percentages
Before diving into the calculation, let's solidify our understanding of percentages. A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "out of one hundred." Therefore, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Method 1: The Direct Calculation Method
This is the most straightforward approach to calculating the percentage. It involves converting the fraction 18/30 into an equivalent fraction with a denominator of 100.
Step 1: Set up the Fraction
We start with the given fraction: 18/30. This represents 18 parts out of a total of 30 parts.
Step 2: Convert to a Decimal
To convert the fraction to a decimal, we divide the numerator (18) by the denominator (30):
18 ÷ 30 = 0.6
Step 3: Convert the Decimal to a Percentage
To express this decimal as a percentage, we multiply it by 100:
0.6 x 100 = 60
Step 4: Add the Percentage Symbol
Finally, we add the percentage symbol (%) to indicate that our result is a percentage:
60%
Therefore, 18 out of 30 is 60%.
Method 2: Simplifying the Fraction First
This method involves simplifying the fraction before converting it to a percentage. Simplifying the fraction often makes the subsequent calculations easier.
Step 1: Find the Greatest Common Divisor (GCD)
The greatest common divisor of 18 and 30 is 6. This means we can divide both the numerator and denominator by 6 without changing the value of the fraction.
Step 2: Simplify the Fraction
Dividing both the numerator and the denominator by 6, we get:
18 ÷ 6 = 3 30 ÷ 6 = 5
The simplified fraction is 3/5.
Step 3: Convert to a Decimal
Now, we divide the numerator (3) by the denominator (5):
3 ÷ 5 = 0.6
Step 4: Convert to a Percentage
Multiply the decimal by 100:
0.6 x 100 = 60
Step 5: Add the Percentage Symbol
Add the percentage symbol:
60%
Again, we arrive at the answer: 18 out of 30 is 60%.
Method 3: Using Proportions
This method uses the concept of proportions to solve the problem. A proportion is a statement that two ratios are equal.
Step 1: Set up the Proportion
We can set up a proportion like this:
18/30 = x/100
Where 'x' represents the percentage we're trying to find.
Step 2: Cross-Multiply
Cross-multiplying the proportion gives us:
30x = 1800
Step 3: Solve for x
Divide both sides of the equation by 30:
x = 1800 ÷ 30 = 60
Therefore, x = 60, meaning 18 out of 30 is 60%.
Practical Applications of Percentage Calculations
The ability to calculate percentages has wide-ranging applications in various aspects of life. Here are a few examples:
1. Financial Calculations:
- Interest rates: Understanding interest rates on loans, savings accounts, and investments requires calculating percentages.
- Discounts: Determining the final price after a discount involves calculating the percentage reduction.
- Taxes: Calculating sales tax, income tax, and other taxes often relies on percentage calculations.
- Profit margins: Businesses use percentage calculations to determine their profit margins.
2. Academic Assessments:
- Grades: Many academic assessments express scores as percentages.
- Test scores: Standardized tests often report results as percentages.
- Coursework: Calculating overall course grades usually involves weighting assignments and expressing them as percentages.
3. Data Analysis and Statistics:
- Surveys and polls: Survey results are often presented as percentages.
- Statistical analysis: Many statistical calculations involve percentages.
- Data visualization: Charts and graphs often use percentages to represent data.
4. Everyday Life:
- Tips and gratuities: Calculating tips in restaurants often involves determining a percentage of the bill.
- Sales and promotions: Understanding discounts and sales requires percentage calculations.
- Recipe scaling: Adjusting recipe ingredients based on the number of servings often involves percentage adjustments.
Expanding Your Understanding: Beyond 18 out of 30
While this guide focuses on 18 out of 30, the principles discussed are applicable to any fraction-to-percentage conversion. To solidify your understanding, practice with different fractions. Try calculating the percentage for various scenarios, such as:
- What is 25 out of 50 as a percentage?
- What is 15 out of 25 as a percentage?
- What is 7 out of 20 as a percentage?
By practicing these calculations, you will strengthen your ability to confidently work with percentages in various contexts.
Conclusion
Calculating what 18 out of 30 represents as a percentage is a straightforward process. Whether you use the direct calculation method, simplify the fraction first, or employ proportions, the result consistently yields 60%. Understanding this fundamental concept is essential for navigating numerous aspects of daily life, from personal finances to professional endeavors. Remember to practice these methods to build confidence and proficiency in percentage calculations. Mastering this skill will empower you to analyze data, make informed decisions, and succeed in various academic and professional settings.
Latest Posts
Latest Posts
-
3 25 Rounded To The Nearest Tenth
May 11, 2025
-
5 To The Power Of Negative 5
May 11, 2025
-
How Big Is 40 Square Meters
May 11, 2025
-
Board And Batten Siding Cost Calculator
May 11, 2025
-
Como Calcular El 7 Por Ciento De Una Cantidad
May 11, 2025
Related Post
Thank you for visiting our website which covers about What Is 18 Out Of 30 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.