What Is 2 2 3 Plus 1 1 2
Treneri
May 13, 2025 · 4 min read
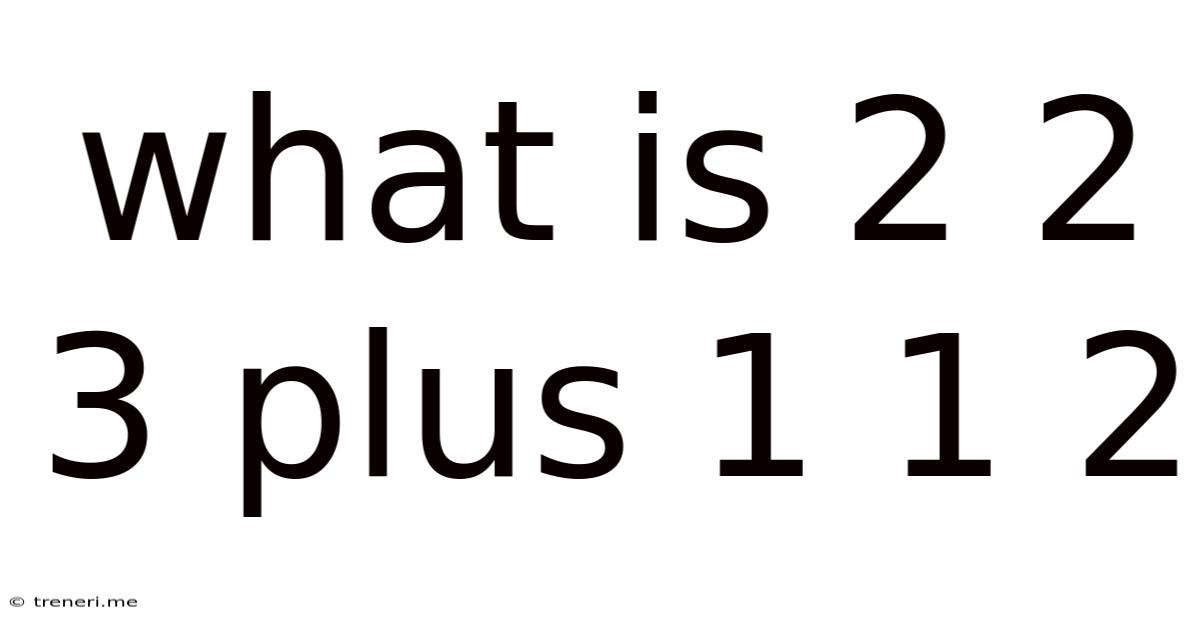
Table of Contents
What is 2 2 3 Plus 1 1 2? Unraveling the Mystery of Number Representation
The seemingly simple question, "What is 2 2 3 plus 1 1 2?" initially presents itself as a straightforward addition problem. However, the unusual representation of the numbers hints at a deeper puzzle involving different number systems or a creative interpretation of mathematical notation. Let's delve into the possibilities and explore the various ways we can approach this intriguing question.
Understanding Different Number Systems
Before jumping into calculations, we need to consider the possibility that "2 2 3" and "1 1 2" aren't standard base-10 representations. Different number systems exist, each using a unique base to represent numbers.
Base-10 (Decimal System)
This is the system we commonly use. It has ten digits (0-9) and each place value represents a power of 10. If "2 2 3" and "1 1 2" are in base-10, the problem is simply:
223 + 112 = 335
However, the unconventional formatting suggests a different interpretation is more likely.
Base-n Systems
In a base-n system, numbers are represented using n distinct digits (0 to n-1). The place values are powers of n. Let's explore some potential base-n interpretations.
Possibility 1: A Base-3 System
If we consider a base-3 system (using digits 0, 1, and 2), then "2 2 3" wouldn't be a valid representation because it contains the digit 3, which doesn't exist in base-3. Similarly, "1 1 2" would be valid. This immediately rules out base-3 as a possibility.
Possibility 2: Exploring Higher Bases
We could explore higher bases, but the problem remains: the digits used seem to suggest a base smaller than 10 but the presence of the digit '3' in the first number complicates matters significantly.
Alternative Interpretations: Beyond Number Systems
Given that straightforward base conversions seem unlikely, we need to consider alternative interpretations of the notation:
Creative Mathematical Interpretations
Could the spaces between the numbers represent a different operation? Could it be concatenation, multiplication, or something more abstract?
Possibility 1: Concatenation
Concatenation involves joining numbers together. If the spaces represent concatenation, then "2 2 3" becomes 223 and "1 1 2" becomes 112. In this case, the problem reduces to:
223 + 112 = 335 (The same result as the initial base-10 assumption)
While this is mathematically valid, it doesn't explain the unusual number formatting.
Possibility 2: Multiple Operations
Perhaps the spaces indicate a sequence of operations. For instance:
- Interpretation A: (2 + 2 + 3) + (1 + 1 + 2) = 7 + 4 = 11
- Interpretation B: (2 * 2 * 3) + (1 * 1 * 2) = 12 + 2 = 14
- Interpretation C: (2^2 * 3) + (1^1 * 2) = 12 + 2 = 14
Possibility 3: A Coding Puzzle
The question might be a simple code where each number represents a letter in the alphabet (A=1, B=2, etc.). This would turn "2 2 3" into "B B C" and "1 1 2" into "A A B". However, without further context or clues, this is pure speculation.
The Importance of Context and Clarification
The ambiguity of the original question highlights the critical role of clear and precise notation in mathematics. Without additional information or context, there's no single definitive answer. The solution depends entirely on the intended interpretation of the unusual number representation.
To solve puzzles like this, it’s vital to:
- Clarify Notation: Always ensure that the mathematical notation is unambiguous. Specify the base if it’s not base-10.
- Define Operations: Clearly state the operations involved. Avoid relying on implicit assumptions.
- Seek Clarification: If there's any ambiguity, don't hesitate to ask for clarification.
Conclusion: The Power of Ambiguity
While we cannot definitively answer "What is 2 2 3 plus 1 1 2?" without further context, exploring the various possibilities highlights the rich variety of interpretations possible within mathematics. It underscores the importance of precise communication and the creativity that can be sparked by seemingly simple problems. The ambiguous nature of the question itself becomes a valuable learning experience, prompting us to think critically about number systems, mathematical operations, and the power of clear notation. It is a reminder that problem-solving often involves interpreting the question as much as solving the equation. The next time you encounter a similar ambiguity, remember the lesson of "2 2 3 plus 1 1 2" – clarity is key!
Latest Posts
Latest Posts
-
How Many Quarts Is 27 Gallons
May 14, 2025
-
How Many Days From January 23 To Today
May 14, 2025
-
What Is The 35th Triangular Number
May 14, 2025
-
How Many Days Since June 17 2022
May 14, 2025
-
What Is 13 8 As A Mixed Number
May 14, 2025
Related Post
Thank you for visiting our website which covers about What Is 2 2 3 Plus 1 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.