What Is 2.5 Percent Of 943
Treneri
May 14, 2025 · 5 min read
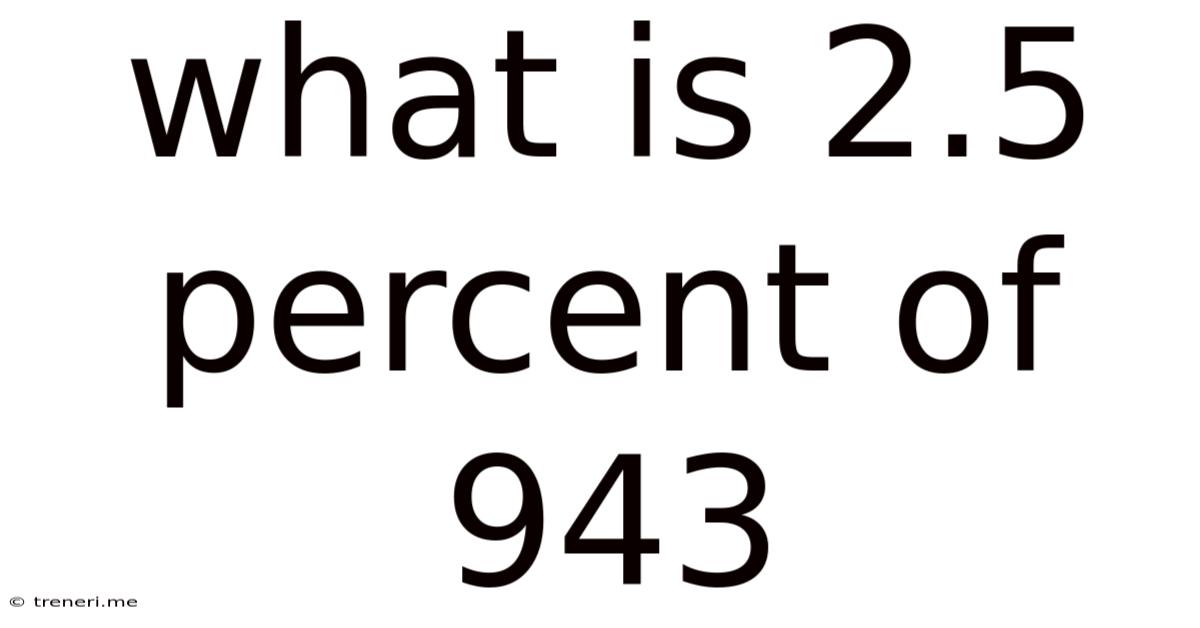
Table of Contents
What is 2.5 Percent of 943? A Deep Dive into Percentage Calculations
Finding 2.5 percent of 943 might seem like a simple calculation, but understanding the underlying principles of percentages opens doors to a world of practical applications, from calculating discounts and taxes to understanding financial statements and analyzing data. This article will not only answer the question directly but also explore the various methods of calculating percentages, delve into the practical uses of percentage calculations, and offer insights into how to approach similar problems confidently.
Understanding Percentages: The Basics
A percentage is simply a fraction expressed as a part of 100. The word "percent" comes from the Latin "per centum," meaning "out of a hundred." Therefore, 2.5 percent means 2.5 parts out of 100. This fundamental understanding is key to solving percentage problems. We can represent this as a fraction (2.5/100) or a decimal (0.025).
Method 1: The Direct Calculation Method
The most straightforward way to calculate 2.5 percent of 943 is to convert the percentage to a decimal and multiply it by the number.
-
Step 1: Convert the percentage to a decimal: 2.5% is equal to 2.5/100 = 0.025
-
Step 2: Multiply the decimal by the number: 0.025 x 943 = 23.575
Therefore, 2.5 percent of 943 is 23.575.
This method is efficient and readily applicable using a calculator or even mental math with practice.
Method 2: The Fractional Method
Another approach involves working with fractions. We can express 2.5 percent as the fraction 2.5/100, which simplifies to 1/40.
-
Step 1: Simplify the fraction: 2.5/100 = 1/40
-
Step 2: Multiply the fraction by the number: (1/40) x 943 = 943/40
-
Step 3: Perform the division: 943/40 = 23.575
This method demonstrates the underlying fractional relationship inherent in percentage calculations. It's particularly useful when dealing with simpler percentages that can be easily converted to manageable fractions.
Method 3: Using Proportions
Proportions offer a powerful and versatile method for solving percentage problems. We set up a proportion where we equate the ratio of the percentage to 100 with the ratio of the unknown value (x) to the total value (943).
-
Step 1: Set up the proportion: 2.5/100 = x/943
-
Step 2: Cross-multiply: 100x = 2.5 * 943
-
Step 3: Solve for x: 100x = 2357.5 => x = 2357.5 / 100 = 23.575
This method highlights the relationship between the percentage, the part, and the whole, making it conceptually clear and applicable to a wide range of percentage problems.
Practical Applications of Percentage Calculations
Understanding percentage calculations extends far beyond simple mathematical exercises. Here are some real-world applications:
-
Finance: Calculating interest earned on savings accounts, determining loan payments, understanding discounts and sales tax, analyzing investment returns, and calculating profit margins all rely heavily on percentage calculations. For example, if a bank offers a 2.5% annual interest rate on a savings account, understanding how to calculate this interest is crucial for financial planning.
-
Sales and Marketing: Businesses use percentages to calculate discounts, markups, and sales commissions. A "25% off" sale requires accurate percentage calculations to determine the final price. Similarly, calculating a salesperson's commission based on a percentage of sales is essential for compensation management.
-
Data Analysis: Percentages are fundamental in data interpretation. Analyzing survey results, understanding market share, and representing data graphically often involve expressing values as percentages. For example, if a survey reveals that 2.5% of respondents prefer a particular product, this percentage provides valuable insights into consumer preferences.
-
Everyday Life: Percentage calculations are encountered in everyday life, such as calculating tips in restaurants, determining the percentage of ingredients in recipes, and understanding discounts on grocery items. These seemingly small calculations cumulatively impact our financial management and decision-making.
Advanced Percentage Calculations: Beyond the Basics
While calculating 2.5% of 943 is straightforward, let's explore some more complex scenarios involving percentages:
-
Finding the percentage increase or decrease: This involves calculating the change in a value as a percentage of the original value. For example, if a product's price increased from 943 to 970, the percentage increase would be calculated as: [(970 - 943) / 943] * 100% ≈ 2.86%.
-
Calculating percentages of percentages: This involves calculating a percentage of a value that is already a percentage of another value. For example, if a store offers a 10% discount on an item already reduced by 20%, you would need to calculate the percentage of the percentage to determine the final price.
-
Solving for the original value: Given a percentage and a resulting value, you can work backward to find the original value. For example, if 2.5% of a value is 23.575, the original value can be found by dividing 23.575 by 0.025.
Tips and Tricks for Mastering Percentage Calculations
-
Memorize common percentage equivalents: Knowing that 25% = 1/4, 50% = 1/2, and 75% = 3/4 can simplify calculations.
-
Use a calculator effectively: Familiarize yourself with the percentage function on your calculator.
-
Practice regularly: The more you practice percentage calculations, the more comfortable and proficient you will become.
-
Break down complex problems: If a problem seems daunting, break it down into smaller, manageable steps.
Conclusion: The Importance of Percentage Calculations in a Data-Driven World
The seemingly simple calculation of 2.5 percent of 943 serves as a gateway to understanding the broader world of percentage calculations. Mastering these calculations is not just about solving mathematical problems; it's about developing a crucial skill applicable to numerous aspects of life, from personal finance to professional endeavors. By understanding the various methods, practical applications, and advanced techniques, you can confidently approach any percentage problem and unlock its valuable insights. The ability to interpret and manipulate percentages is an increasingly vital skill in our data-driven world, empowering informed decision-making in various contexts. Remember to practice regularly and apply your knowledge to real-world scenarios to further enhance your proficiency.
Latest Posts
Latest Posts
-
What Is 17 Out Of 20 As A Grade
May 14, 2025
-
How Many Oz In 59 Ml
May 14, 2025
-
How High Does Uv Have To Be To Tan
May 14, 2025
-
What Is 90 Days From August 1st 2024
May 14, 2025
-
How Many Days Is 246 Hours
May 14, 2025
Related Post
Thank you for visiting our website which covers about What Is 2.5 Percent Of 943 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.