What Is 2 Percent Of 10
Treneri
May 09, 2025 · 5 min read
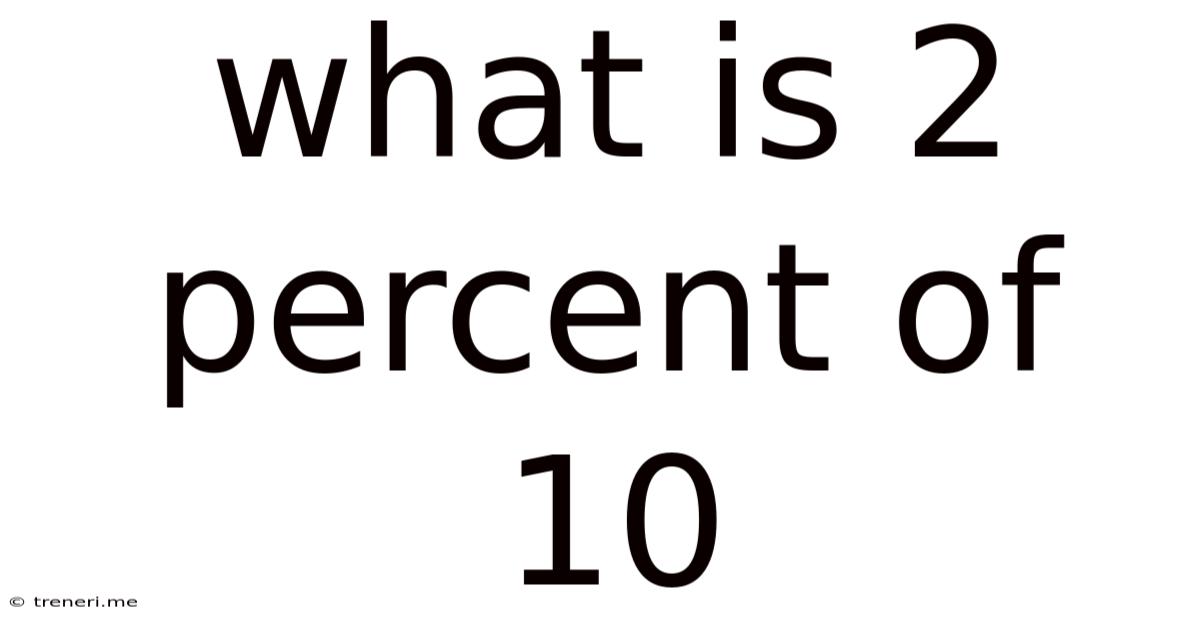
Table of Contents
What is 2 Percent of 10? A Deep Dive into Percentages and Their Applications
Calculating percentages is a fundamental skill applicable across numerous fields, from everyday budgeting and shopping to complex financial analyses and scientific research. Understanding how to calculate percentages not only empowers you to solve everyday problems but also enhances your comprehension of data presented in various formats. This article delves into the seemingly simple question, "What is 2 percent of 10?", but expands it to provide a comprehensive understanding of percentages, their calculation, and their practical uses.
Understanding Percentages: The Basics
A percentage is a fraction or ratio expressed as a number out of 100. The word "percent" literally means "out of one hundred" ( per cent). Therefore, 2 percent means 2 out of 100, or 2/100. This can be represented as a decimal (0.02) or a fraction (2/100, which simplifies to 1/50). Understanding these different representations is crucial for performing percentage calculations effectively.
Key Concepts:
- Percentage: The ratio expressed as a number out of 100.
- Base Value: The original number from which the percentage is calculated (in our case, 10).
- Percentage Value: The result of the percentage calculation (the answer to "What is 2 percent of 10?").
Calculating 2 Percent of 10: Three Methods
There are several ways to calculate 2 percent of 10. We'll explore three common methods:
Method 1: Using the Decimal Equivalent
This method involves converting the percentage to its decimal equivalent and multiplying it by the base value.
- Convert the percentage to a decimal: 2% is equivalent to 0.02 (divide 2 by 100).
- Multiply the decimal by the base value: 0.02 * 10 = 0.2
Therefore, 2 percent of 10 is 0.2.
Method 2: Using the Fraction Equivalent
This method utilizes the fractional representation of the percentage.
- Convert the percentage to a fraction: 2% is equivalent to 2/100.
- Simplify the fraction (if possible): 2/100 simplifies to 1/50.
- Multiply the fraction by the base value: (1/50) * 10 = 10/50 = 1/5 = 0.2
Again, 2 percent of 10 is 0.2.
Method 3: Using Proportions
This method uses the concept of proportions to solve for the unknown percentage value.
We can set up a proportion:
2/100 = x/10
Where 'x' represents the unknown value (2 percent of 10). To solve for 'x', we cross-multiply:
100x = 20
x = 20/100 = 0.2
Thus, 2 percent of 10 is 0.2.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is vital in numerous real-world scenarios:
1. Finance and Budgeting:
- Interest Rates: Calculating simple and compound interest requires understanding percentages. For example, determining the interest earned on a savings account or the interest paid on a loan.
- Discounts and Sales Tax: Determining the final price of an item after a discount or adding sales tax involves percentage calculations. A common example is calculating the final price of an item on sale.
- Investment Returns: Investors use percentages to track their investment performance, comparing returns against initial investments.
- Budgeting: Individuals and businesses use percentages to allocate funds across various budget categories.
2. Everyday Shopping:
- Sales and Discounts: Understanding percentage discounts helps consumers make informed purchasing decisions.
- Tips and Gratuities: Calculating appropriate tips in restaurants often involves estimating a percentage of the bill.
- Comparing Prices: Percentages help compare the prices of different products, identifying the best value for money.
3. Science and Research:
- Data Analysis: Scientists use percentages extensively to represent data, analyze trends, and draw conclusions. For example, expressing experimental error or success rates.
- Statistical Analysis: Many statistical calculations, such as calculating confidence intervals, involve percentages.
4. Education and Assessment:
- Grade Calculations: Grades are often expressed as percentages to represent a student's performance relative to the total possible score.
- Test Scores: Test scores are frequently presented as percentages, indicating the proportion of questions answered correctly.
5. Business and Marketing:
- Market Share: Businesses track their market share, expressing it as a percentage of the total market size.
- Profit Margins: Calculating profit margins helps businesses understand their profitability.
- Sales Growth: Companies use percentage changes to track sales growth over time.
Beyond the Basics: More Complex Percentage Calculations
While calculating 2 percent of 10 is relatively straightforward, many situations involve more complex percentage calculations. These can include:
- Calculating the percentage increase or decrease between two numbers: This involves finding the difference between the two numbers, dividing by the original number, and then multiplying by 100.
- Finding the original value when a percentage and the resulting value are known: This requires working backwards from the percentage and resulting value to find the original number.
- Calculating compound percentages: This involves calculating percentages repeatedly, taking into account the effect of previous percentage changes.
Mastering Percentages: Tools and Resources
Several resources can aid in mastering percentage calculations:
- Online Calculators: Many online calculators are available to perform various percentage calculations quickly and easily.
- Spreadsheet Software: Spreadsheet programs like Microsoft Excel or Google Sheets provide built-in functions for performing percentage calculations.
- Educational Websites and Videos: Numerous websites and videos provide tutorials and examples to improve understanding of percentages.
Conclusion: The Significance of Percentage Calculations
The seemingly simple calculation of "What is 2 percent of 10?" underscores the broader significance of understanding percentages. From managing personal finances to analyzing scientific data, the ability to perform percentage calculations is a valuable skill applicable across a wide range of disciplines. By mastering these fundamental concepts, individuals enhance their ability to interpret data, make informed decisions, and succeed in various aspects of life. This comprehensive understanding moves beyond simply finding the answer (0.2) and instead empowers you to approach and solve a wider spectrum of percentage-related problems. Remember, practice is key, and with consistent effort, you can become proficient in calculating and utilizing percentages effectively.
Latest Posts
Latest Posts
-
19 Out Of 23 As A Grade
May 10, 2025
-
How Many Miles Is 9000 Km
May 10, 2025
-
2 5 3 4 As A Fraction
May 10, 2025
-
Furnace Size Calculator By Zip Code
May 10, 2025
-
How Many Teaspoons Is 1 4 Ounce Of Yeast
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Is 2 Percent Of 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.