What Is 2 To The Power Of 9
Treneri
May 13, 2025 · 5 min read
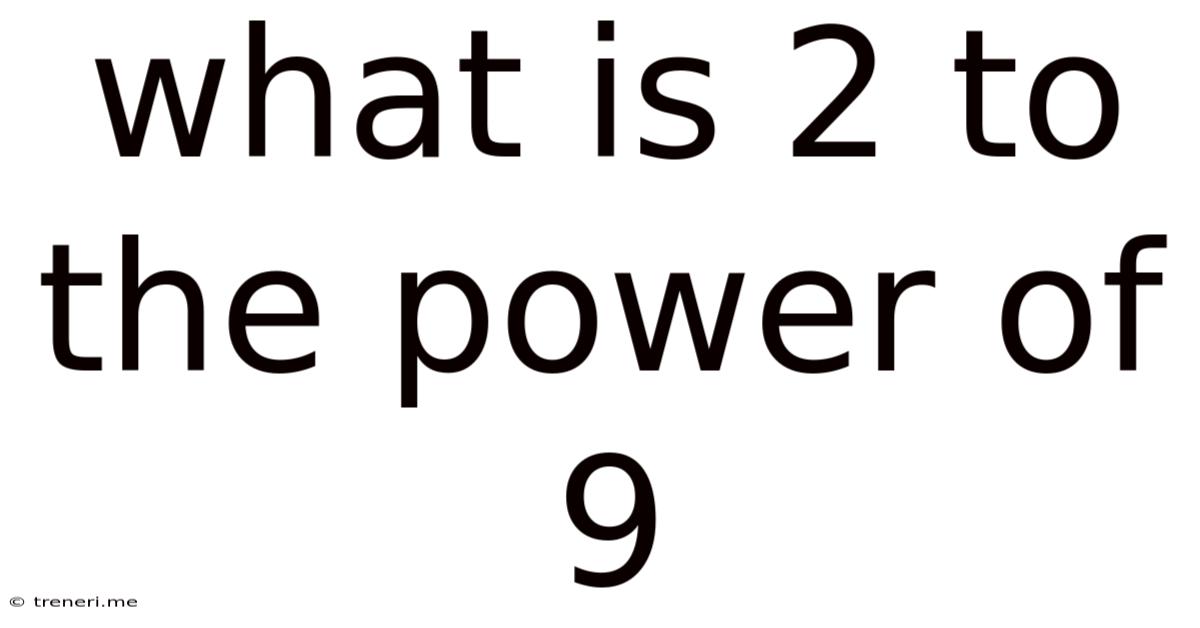
Table of Contents
What is 2 to the Power of 9? Exploring Exponential Growth and its Applications
This seemingly simple question, "What is 2 to the power of 9?", opens the door to a fascinating exploration of exponential growth, its mathematical underpinnings, and its widespread applications in various fields. Let's delve into the answer and uncover the broader implications of this fundamental concept.
Understanding Exponential Notation
Before we tackle 2 to the power of 9, let's solidify our understanding of exponential notation. When we see a number expressed as a<sup>b</sup>, it means that a is multiplied by itself b times. In other words, it represents repeated multiplication. For example:
- 2<sup>2</sup> = 2 x 2 = 4 (2 squared or 2 to the power of 2)
- 2<sup>3</sup> = 2 x 2 x 2 = 8 (2 cubed or 2 to the power of 3)
- 2<sup>4</sup> = 2 x 2 x 2 x 2 = 16 (2 to the power of 4)
And so on. This pattern of repeated multiplication is what characterizes exponential growth – a growth rate that's proportional to the current value.
Calculating 2 to the Power of 9
Now, let's address the question directly: What is 2 to the power of 9? Using the definition of exponential notation, we can calculate this as follows:
2<sup>9</sup> = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 = 512
Therefore, 2 to the power of 9 is 512.
The Significance of Exponential Growth
The seemingly simple calculation of 2<sup>9</sup> highlights a crucial characteristic of exponential growth: its rapid acceleration. While the initial increases might seem modest, the growth quickly becomes dramatic. This is because each subsequent multiplication builds upon the previous result, leading to a compounding effect.
This principle is central to understanding a wide array of phenomena, from compound interest in finance to the spread of viral infections in epidemiology, and the growth of populations in ecology. Let's look at some real-world examples:
1. Compound Interest: The Power of Exponential Growth in Finance
Imagine investing a small amount of money at a fixed interest rate that compounds annually. Each year, the interest earned is added to the principal, and the interest for the next year is calculated on the larger amount. This compounding effect leads to exponential growth of your investment over time. The longer the investment period, the more significant the impact of exponential growth becomes.
2. Population Growth: Modeling Exponential Expansion
Population growth often follows an exponential pattern, especially in environments with abundant resources and low mortality rates. Each generation contributes to the overall population size, leading to a multiplicative increase in subsequent generations. While real-world population growth often faces limitations (such as resource scarcity or disease), the underlying principle of exponential growth is a significant factor in understanding population dynamics.
3. Viral Spread: Understanding Exponential Transmission
The spread of viral infections can be modeled using exponential growth, especially in the early stages of an outbreak. Each infected individual can transmit the virus to multiple others, leading to a rapid increase in the number of infected individuals. Understanding this exponential pattern is crucial for public health officials in implementing effective control measures, such as vaccination and quarantine.
4. Technological Advancements: Moore's Law and Exponential Progress
Moore's Law, an observation in the semiconductor industry, posits that the number of transistors on a microchip doubles approximately every two years. This exponential growth in computing power has fueled remarkable advancements in technology, leading to smaller, faster, and more powerful devices. This rapid pace of technological progress has profoundly impacted numerous aspects of modern life.
Beyond 2 to the Power of 9: Exploring Larger Exponents
While we've focused on 2<sup>9</sup>, the concept of exponential growth extends to much larger exponents. Consider 2<sup>10</sup> (1024), 2<sup>20</sup> (over a million), and beyond. As the exponent increases, the resulting value grows astronomically. This highlights the immense power of exponential functions and their ability to model rapid growth and change. These higher powers are relevant in:
- Computer Science: Data storage and processing often involve numbers with very large exponents.
- Cryptography: Large exponential calculations form the basis of secure encryption algorithms.
- Physics: Exponential functions describe radioactive decay and other natural phenomena.
Practical Applications and Real-World Scenarios
Understanding exponential growth isn't just an abstract mathematical exercise. It's a vital tool for making predictions, analyzing trends, and making informed decisions in various fields. Here are some practical examples:
- Financial Planning: Calculating future investment values, determining loan repayments, and managing retirement funds all rely heavily on exponential growth models.
- Epidemiology: Predicting the spread of infectious diseases, assessing the effectiveness of public health interventions, and allocating resources effectively during outbreaks all involve the use of exponential models.
- Environmental Science: Modeling population growth, predicting resource depletion, and assessing the impact of climate change often require understanding exponential growth patterns.
- Business Analysis: Analyzing market trends, forecasting sales, and planning for future growth all utilize exponential models.
Conclusion: The Enduring Power of Exponential Growth
The answer to "What is 2 to the power of 9?" is 512. However, the true significance of this calculation lies in the broader understanding of exponential growth it unlocks. This fundamental concept permeates numerous aspects of our world, shaping technological advancements, influencing economic trends, impacting public health, and driving ecological processes. Understanding exponential growth empowers us to make better predictions, design more effective strategies, and solve complex problems across a wide range of fields. From the simple calculation of 2<sup>9</sup>, we've ventured into a world of immense growth and profound implications. The power of exponential growth continues to shape our understanding of the world around us, driving innovation, progress, and a deeper appreciation of the mathematical underpinnings of our reality.
Latest Posts
Latest Posts
-
170 Grams Is How Many Pounds
May 14, 2025
-
4 5 3 4 As A Fraction
May 14, 2025
-
How Many Pounds In A Gallon Of Gas
May 14, 2025
-
Cuanto Es 8 Libras En Kg
May 14, 2025
-
How Many Quarts Is 27 Gallons
May 14, 2025
Related Post
Thank you for visiting our website which covers about What Is 2 To The Power Of 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.