What Is 20/30 As A Percent
Treneri
May 14, 2025 · 5 min read
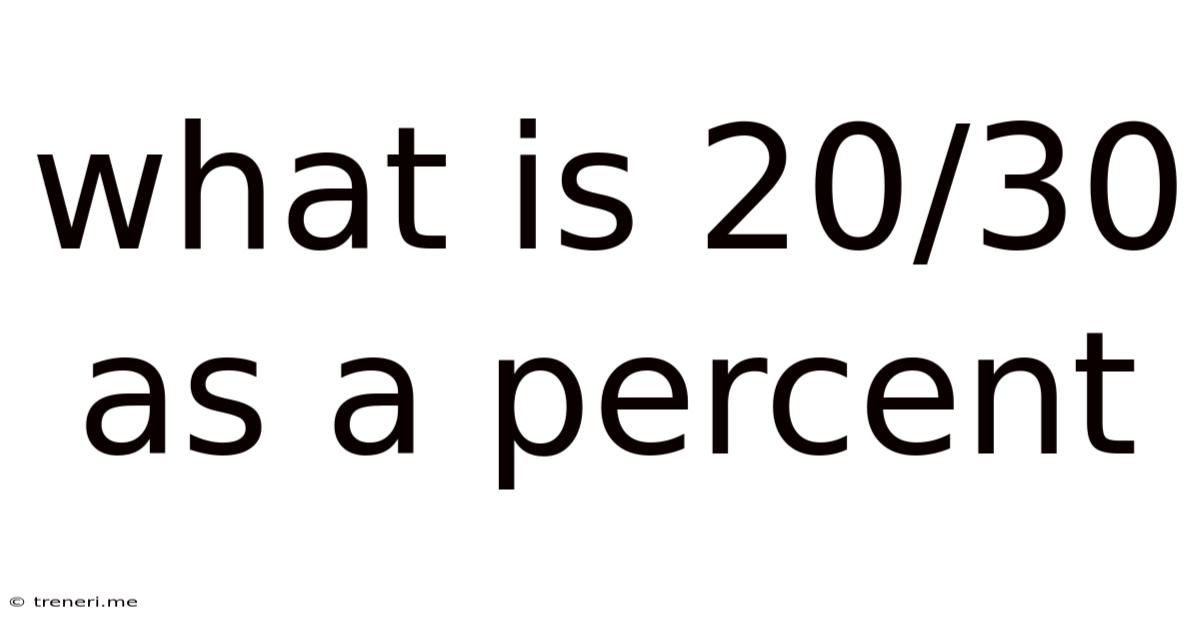
Table of Contents
What is 20/30 as a Percent? A Comprehensive Guide to Fraction-to-Percentage Conversion
Converting fractions to percentages is a fundamental skill in mathematics with widespread applications in various fields, from finance and statistics to everyday life. Understanding this conversion process empowers you to easily interpret and compare proportions, making informed decisions in diverse situations. This comprehensive guide delves into the intricacies of converting 20/30 to a percentage, providing a step-by-step explanation and exploring broader concepts of fraction-to-percentage conversion.
Understanding Fractions and Percentages
Before diving into the specific conversion of 20/30, let's solidify our understanding of fractions and percentages.
Fractions: Representing Parts of a Whole
A fraction represents a part of a whole. It consists of two parts:
- Numerator: The top number, indicating the number of parts being considered.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 20/30, 20 is the numerator and 30 is the denominator. This means we are considering 20 parts out of a total of 30 equal parts.
Percentages: Expressing Parts per Hundred
A percentage represents a fraction out of 100. The term "percent" literally means "per hundred" (from Latin per centum). Percentages provide a standardized way to compare proportions, making them incredibly useful for various applications.
Converting 20/30 to a Percentage: A Step-by-Step Guide
Converting a fraction to a percentage involves two primary steps:
Step 1: Convert the fraction to a decimal.
To convert the fraction 20/30 to a decimal, we divide the numerator (20) by the denominator (30):
20 ÷ 30 = 0.666...
The result is a recurring decimal, meaning the digit 6 repeats infinitely. For practical purposes, we can round this to a certain number of decimal places. We'll use three decimal places for now: 0.667.
Step 2: Convert the decimal to a percentage.
To convert a decimal to a percentage, we multiply the decimal by 100 and add the percent symbol (%):
0.667 x 100 = 66.7%
Therefore, 20/30 is equal to 66.7% (rounded to one decimal place).
Simplifying Fractions Before Conversion: A More Efficient Approach
Before converting 20/30 to a percentage, we can simplify the fraction to make the calculation easier. Both 20 and 30 are divisible by 10:
20 ÷ 10 = 2 30 ÷ 10 = 3
So, 20/30 simplifies to 2/3.
Now, we can convert 2/3 to a decimal:
2 ÷ 3 = 0.666...
And then to a percentage:
0.666... x 100 = 66.666...%
Rounding to one decimal place, we again arrive at 66.7%. Simplifying the fraction first often leads to a more manageable calculation, especially with larger numbers.
Real-World Applications of Fraction-to-Percentage Conversion
The ability to convert fractions to percentages is crucial in many real-world scenarios. Here are a few examples:
- Calculating Discounts: A store offering a 20/30 (or 2/3) discount on an item effectively offers a 66.7% discount.
- Analyzing Test Scores: If you answered 20 out of 30 questions correctly on a test, your score is 66.7%.
- Understanding Financial Data: Financial reports frequently use percentages to represent proportions of profits, losses, or market share. Converting fractions to percentages allows for easier comparison and interpretation of this data.
- Scientific Research: Scientists use percentages extensively to represent data and results from experiments.
- Everyday Life: From calculating tips in restaurants to understanding sales tax, percentages are a ubiquitous part of our daily lives.
Beyond 20/30: Mastering Fraction-to-Percentage Conversion
The method outlined above for converting 20/30 to a percentage applies equally to any fraction. Here's a generalized approach:
- Simplify the fraction (if possible): Reduce the fraction to its simplest form by dividing both the numerator and denominator by their greatest common divisor.
- Divide the numerator by the denominator: This gives you the decimal equivalent of the fraction.
- Multiply the decimal by 100: This converts the decimal to a percentage.
- Add the percent symbol (%): This completes the conversion.
Handling Recurring Decimals: Precision and Rounding
As we saw with 2/3, some fractions produce recurring decimals. When dealing with recurring decimals in percentage calculations, it’s important to:
- Specify the level of precision: Decide how many decimal places you need for your application. Using more decimal places generally increases accuracy but can also make the numbers more cumbersome.
- Use appropriate rounding techniques: Rounding methods like rounding to the nearest tenth, hundredth, or thousandth ensure consistency and clarity in your results.
Advanced Concepts and Related Topics
The conversion of fractions to percentages is a foundational concept that opens the door to more advanced mathematical ideas, including:
- Ratio and Proportion: Fractions and percentages are intimately connected to the concepts of ratio and proportion. Understanding these concepts deepens your comprehension of relative quantities and their comparisons.
- Statistical Analysis: Percentages are essential in statistical analysis, enabling comparisons across different datasets and aiding in the interpretation of data patterns.
- Financial Modeling: Accurate fraction-to-percentage conversion is vital in building financial models, allowing for precise predictions and risk assessments.
- Data Visualization: Representing data using percentages (e.g., in pie charts or bar graphs) improves the clarity and impact of data visualization efforts.
Conclusion
Converting 20/30 to a percentage is a straightforward process once you grasp the underlying principles of fractions and percentages. By understanding these principles, and by mastering the techniques of simplification, decimal conversion, and rounding, you can confidently tackle fraction-to-percentage conversions in various contexts. This skill enhances your mathematical literacy and equips you to interpret and utilize data effectively in your professional and personal life. Remember that accurate calculation and clear communication of results are key when working with percentages.
Latest Posts
Latest Posts
-
How Many Pounds In 18 Oz
May 14, 2025
-
How Far Apart Should Railing Spindles Be
May 14, 2025
-
1975 To 2023 How Many Years
May 14, 2025
-
My Dog Ate A Few Raisins
May 14, 2025
-
1 1 2 Minus 3 4
May 14, 2025
Related Post
Thank you for visiting our website which covers about What Is 20/30 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.