What Is 24 Out Of 40 As A Percentage
Treneri
May 12, 2025 · 5 min read
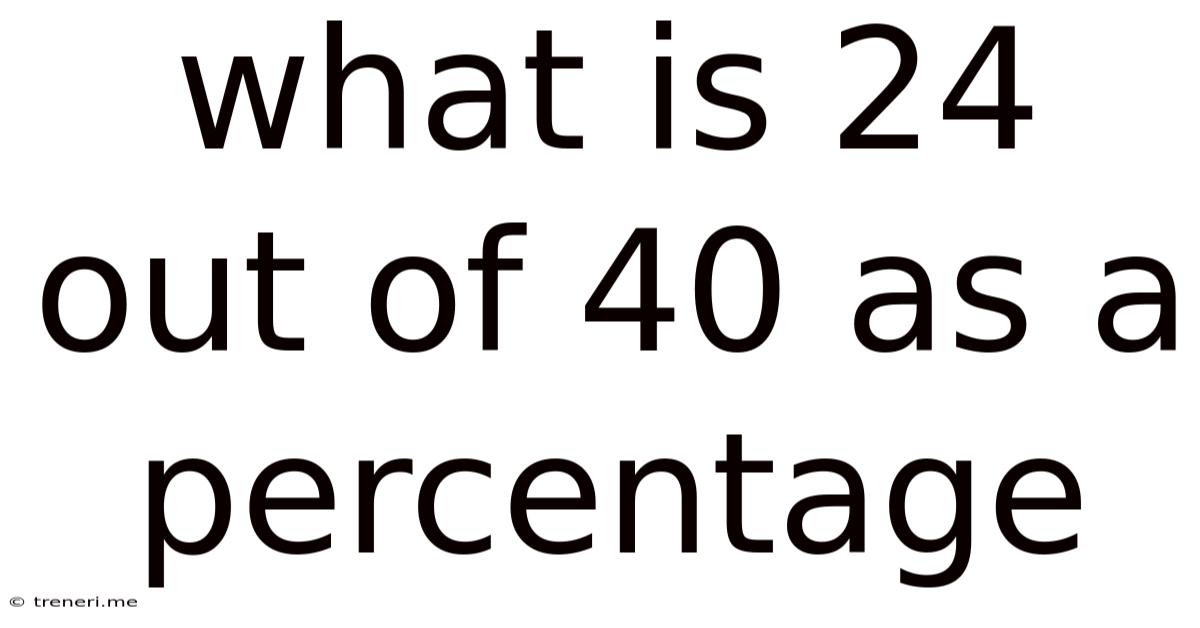
Table of Contents
What is 24 out of 40 as a Percentage? A Comprehensive Guide
Calculating percentages is a fundamental skill applicable across numerous fields, from everyday budgeting to complex statistical analysis. Understanding how to convert fractions into percentages is crucial for interpreting data and making informed decisions. This article delves into the process of calculating "24 out of 40 as a percentage," explaining the method step-by-step and exploring related concepts to solidify your understanding.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "out of one hundred." The symbol used to represent percentage is %. Therefore, 25% means 25 out of 100, or 25/100.
Calculating 24 out of 40 as a Percentage: The Step-by-Step Method
To determine what 24 out of 40 represents as a percentage, we follow these simple steps:
Step 1: Express the given values as a fraction.
The problem "24 out of 40" can be expressed as a fraction: 24/40.
Step 2: Convert the fraction to a decimal.
To convert a fraction to a decimal, divide the numerator (the top number) by the denominator (the bottom number):
24 ÷ 40 = 0.6
Step 3: Convert the decimal to a percentage.
To convert a decimal to a percentage, multiply the decimal by 100 and add the percentage symbol (%):
0.6 x 100 = 60%
Therefore, 24 out of 40 is equal to 60%.
Simplifying the Fraction Before Conversion (Optional but Recommended)
While the above method is perfectly valid, simplifying the fraction before converting to a decimal can make the calculation easier. Let's simplify 24/40:
Both 24 and 40 are divisible by 8:
24 ÷ 8 = 3 40 ÷ 8 = 5
This simplifies the fraction to 3/5.
Now, convert 3/5 to a decimal:
3 ÷ 5 = 0.6
Finally, convert the decimal to a percentage:
0.6 x 100 = 60%
As you can see, we arrive at the same answer, 60%, regardless of whether we simplify the fraction first. However, simplifying often makes the division simpler, particularly with larger numbers.
Practical Applications of Percentage Calculations
The ability to calculate percentages has widespread applications:
1. Academic Performance:
Calculating grades, test scores, and overall academic performance often involves percentage calculations. For example, if you answered 24 questions correctly out of 40 on a test, your score would be 60%.
2. Financial Management:
Percentages are essential in managing personal and business finances. Calculating interest rates, discounts, taxes, profit margins, and investment returns all rely on percentage calculations. Understanding percentage changes is crucial for tracking financial performance.
3. Data Analysis and Statistics:
In statistics, percentages are used to represent proportions, frequencies, and probabilities. Analyzing datasets often involves calculating percentages to summarize and interpret data effectively. Understanding percentage changes helps in tracking trends and identifying significant variations.
4. Sales and Marketing:
Percentages are heavily used in sales and marketing. Calculating sales growth, conversion rates, market share, and discounts all require proficiency in percentage calculations. This information is key to optimizing marketing strategies and sales performance.
5. Everyday Life:
Calculating tips, discounts at stores, and understanding sales promotions all involve percentage calculations, highlighting the everyday relevance of this skill.
Beyond the Basics: Understanding Percentage Increase and Decrease
Beyond simply converting fractions to percentages, understanding percentage changes is crucial. This involves calculating the percentage increase or decrease between two values.
Percentage Increase:
The formula for calculating percentage increase is:
[(New Value - Old Value) / Old Value] x 100%
Percentage Decrease:
The formula for calculating percentage decrease is:
[(Old Value - New Value) / Old Value] x 100%
For instance, if your initial score was 20 out of 40 (50%), and you improved to 24 out of 40 (60%), the percentage increase would be:
[(60% - 50%) / 50%] x 100% = 20%
Advanced Percentage Calculations: Dealing with More Complex Scenarios
While calculating "24 out of 40 as a percentage" is a straightforward example, more complex scenarios may arise. These might include:
- Calculating percentages of percentages: Finding a certain percentage of a percentage value.
- Calculating percentages with multiple variables: Involving several percentage changes or values.
- Using percentages in compound interest calculations: Determining the total value after several years of interest accumulation.
Mastering these basic percentage calculations forms a strong foundation for tackling more complex problems. Consistent practice and a firm grasp of the underlying concepts are key to success.
Troubleshooting Common Mistakes
When working with percentages, several common mistakes can occur:
- Incorrect Fraction Formation: Ensure the correct numerator (the part) and denominator (the whole) are identified before converting to a decimal.
- Decimal Point Errors: Pay close attention to decimal points when converting between decimals and percentages. Incorrect placement can lead to significant errors.
- Misunderstanding Percentage Change: Clearly distinguish between percentage points and percentage changes. A change from 50% to 60% is a 20% increase, not a 10% increase.
- Rounding Errors: Be mindful of rounding during calculations to maintain accuracy, particularly in financial or statistical applications.
Conclusion
Calculating "24 out of 40 as a percentage" is a simple yet fundamental skill with widespread applications. By understanding the step-by-step process, simplifying fractions, and recognizing potential errors, you can confidently handle percentage calculations in various contexts. From academic assessments to financial management and data analysis, mastering percentages is an invaluable asset. Regular practice and the application of these techniques will enhance your proficiency and confidence in handling percentage-related problems. Remember that even complex percentage calculations build upon this fundamental understanding, so a strong foundation here is crucial for tackling more advanced scenarios.
Latest Posts
Latest Posts
-
If You Was Born In 1996 How Old Are You
May 15, 2025
-
What Is The Greatest Common Factor Of 15 And 50
May 15, 2025
-
What Grade Is 9 Out Of 15
May 15, 2025
-
Tiempo De Embarazo De Un Gato
May 15, 2025
-
How To Convert Slope Intercept Form To Point Slope Form
May 15, 2025
Related Post
Thank you for visiting our website which covers about What Is 24 Out Of 40 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.