What Is 25 Off Of $10
Treneri
May 10, 2025 · 4 min read
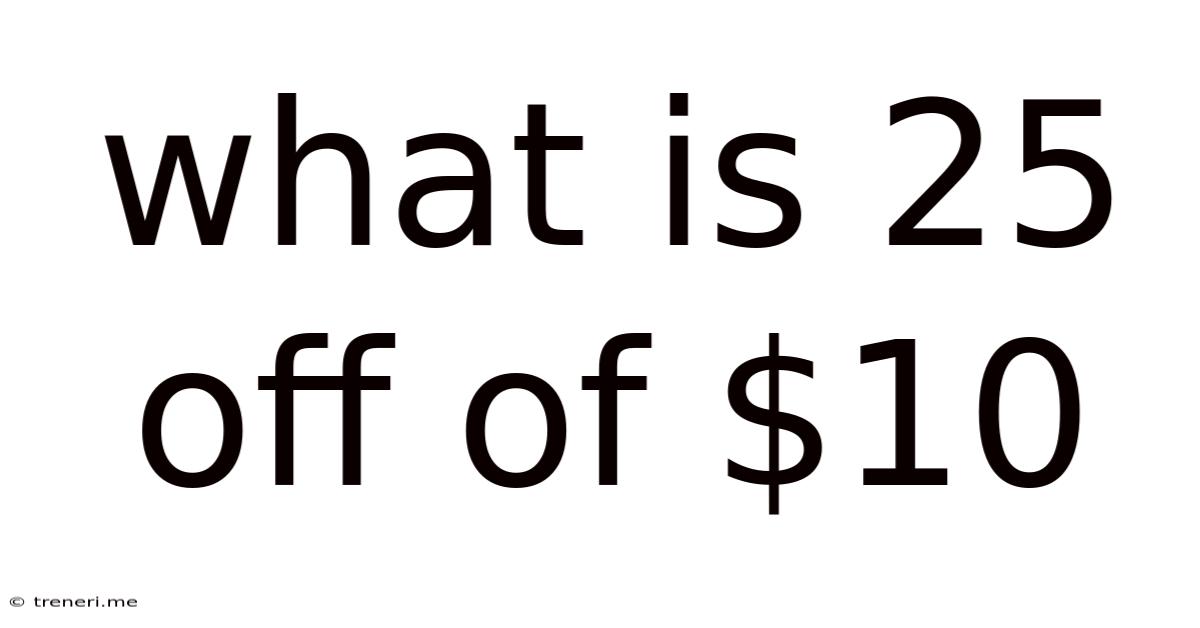
Table of Contents
What is 25% Off of $10? A Comprehensive Guide to Percentage Calculations
Calculating discounts is a fundamental skill in everyday life, whether you're shopping for groceries, comparing prices, or understanding financial statements. This article dives deep into how to calculate 25% off of $10, explaining the process step-by-step and exploring various methods to arrive at the correct answer. We'll also cover broader percentage calculation strategies, making you confident in tackling similar problems in the future.
Understanding Percentages
Before we tackle the specific problem, let's clarify what a percentage represents. A percentage is a fraction of 100. For example, 25% means 25 out of 100, or 25/100, which simplifies to 1/4. This means 25% represents one-quarter of a whole.
Method 1: Using the Decimal Equivalent
This is arguably the most straightforward method. To find 25% of $10, we first convert the percentage into its decimal equivalent. We do this by dividing the percentage by 100:
25% ÷ 100 = 0.25
Now, we simply multiply this decimal by the original price:
0.25 × $10 = $2.50
This means a 25% discount on $10 is $2.50. Therefore, the final price after the discount is:
$10 - $2.50 = $7.50
Method 2: Using Fractions
As mentioned earlier, 25% is equivalent to the fraction 1/4. This provides an alternative approach:
1/4 × $10 = $2.50
This calculation directly gives us the discount amount. Subtracting this from the original price yields the final price:
$10 - $2.50 = $7.50
Method 3: Proportions
This method utilizes the concept of proportions, setting up a ratio to solve for the unknown discount amount. We can set up the following proportion:
25/100 = x/$10
Where 'x' represents the discount amount. To solve for 'x', we cross-multiply:
100x = 25 × 10
100x = 250
x = 250 ÷ 100
x = $2.50
Again, we subtract this discount from the original price to find the final price:
$10 - $2.50 = $7.50
Applying this Knowledge: Real-world Examples
Understanding percentage calculations is crucial in various real-world scenarios. Let's explore some examples:
Shopping Discounts:
Imagine you're buying a shirt originally priced at $20, and it's on sale with a 30% discount. Using the decimal method:
30% ÷ 100 = 0.30
0.30 × $20 = $6 (discount amount)
$20 - $6 = $14 (final price)
Sales Tax Calculations:
Sales tax is added to the original price, increasing the final cost. Let's say the sales tax in your area is 8%, and you're buying an item for $50.
8% ÷ 100 = 0.08
0.08 × $50 = $4 (sales tax amount)
$50 + $4 = $54 (final price)
Interest Calculations:
Interest calculations are frequently encountered in finance. If you have a savings account with an annual interest rate of 4% and a balance of $1000, the interest earned in a year would be:
4% ÷ 100 = 0.04
0.04 × $1000 = $40 (interest earned)
Tip Calculations:
When dining out, it's customary to leave a tip for the server. If you want to leave a 15% tip on a $60 bill:
15% ÷ 100 = 0.15
0.15 × $60 = $9 (tip amount)
$60 + $9 = $69 (total cost)
Beyond the Basics: Advanced Percentage Calculations
While the examples above showcase common percentage calculations, more complex scenarios can arise. These might involve calculating percentage increase or decrease over time, or determining the percentage change between two values.
Percentage Increase:
If a value increases from an initial value to a final value, the percentage increase is calculated as follows:
[(Final Value - Initial Value) / Initial Value] × 100
For instance, if your salary increases from $40,000 to $45,000:
[($45,000 - $40,000) / $40,000] × 100 = 12.5% increase
Percentage Decrease:
Similarly, if a value decreases, the percentage decrease is:
[(Initial Value - Final Value) / Initial Value] × 100
If the price of a product decreases from $80 to $60:
[($80 - $60) / $80] × 100 = 25% decrease
Mastering Percentage Calculations: Tips and Tricks
To become proficient in calculating percentages, consider these helpful tips:
- Memorize common percentage equivalents: Knowing that 25% = 1/4, 50% = 1/2, and 75% = 3/4 can significantly speed up calculations.
- Use a calculator: For more complex calculations, a calculator can save time and reduce the risk of errors.
- Practice regularly: The more you practice, the more comfortable and efficient you'll become.
- Understand the context: Always carefully read the problem to ensure you're calculating the correct percentage. Are you finding a discount, a tax amount, or something else?
- Check your work: Always double-check your calculations to ensure accuracy.
Conclusion: The Power of Percentage Calculations
Understanding percentage calculations is an essential skill applicable across numerous aspects of daily life. From shopping to finance, the ability to quickly and accurately calculate percentages empowers informed decision-making. By mastering the different methods and utilizing helpful tips, you can confidently tackle percentage problems of varying complexities, enhancing your financial literacy and overall problem-solving skills. Remember, consistent practice is key to mastering this fundamental mathematical concept. The seemingly simple question, "What is 25% off of $10?" opens the door to a vast understanding of percentage-based calculations with real-world applications.
Latest Posts
Latest Posts
-
How Many Days Is 370 Hours
May 10, 2025
-
Round 755 To The Nearest Ten
May 10, 2025
-
Mcg Or Mg Which Is More
May 10, 2025
-
Calculate The Area Of The Figure Below
May 10, 2025
-
How Many Hours Is 59 Days
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Is 25 Off Of $10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.