What Is 3/8 + 1/3 In Fraction Form
Treneri
May 13, 2025 · 5 min read
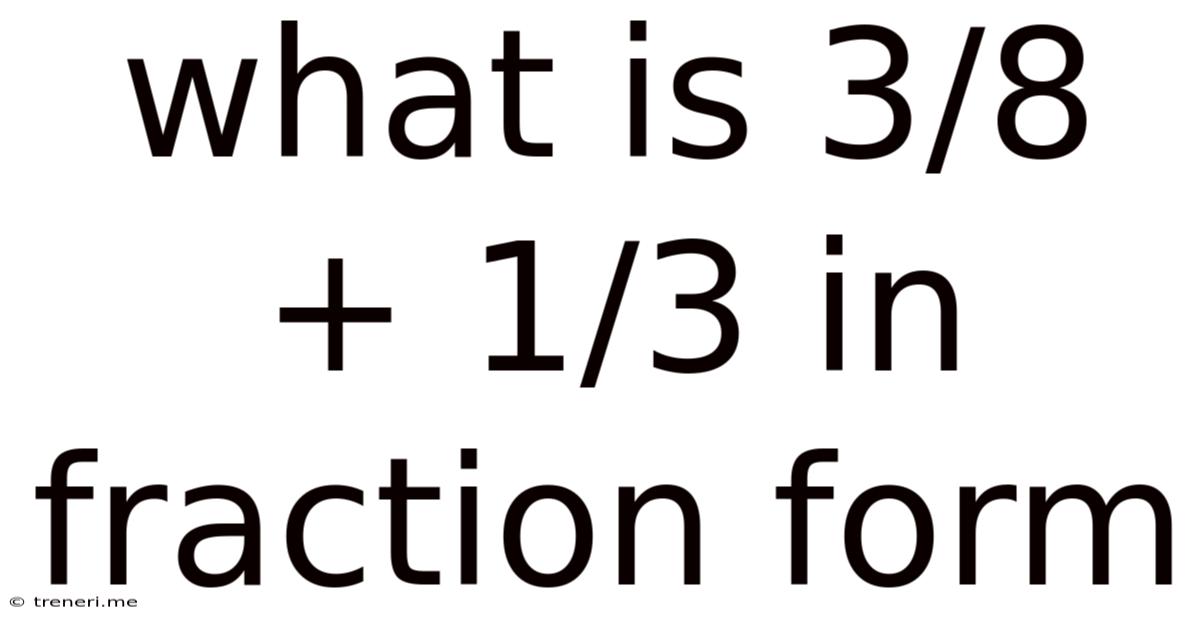
Table of Contents
What is 3/8 + 1/3 in Fraction Form? A Comprehensive Guide
Adding fractions might seem simple at first glance, but mastering the process, especially when dealing with fractions with different denominators, requires a solid understanding of fundamental mathematical concepts. This comprehensive guide will walk you through adding 3/8 and 1/3, explaining the steps involved and providing valuable insights into fraction addition in general. We’ll also explore related concepts and offer tips for solving similar problems.
Understanding Fractions
Before we dive into the addition problem, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two main parts:
- Numerator: The top number represents the number of parts we have.
- Denominator: The bottom number represents the total number of equal parts the whole is divided into.
For instance, in the fraction 3/8, 3 is the numerator (we have 3 parts), and 8 is the denominator (the whole is divided into 8 equal parts).
Adding Fractions with Different Denominators
The core challenge in adding 3/8 and 1/3 lies in their different denominators. We cannot directly add fractions unless they share the same denominator (a common denominator). The process involves finding the least common denominator (LCD) and then adjusting the fractions accordingly.
Finding the Least Common Denominator (LCD)
The LCD is the smallest number that is a multiple of both denominators (8 and 3 in our case). Several methods exist to find the LCD, including:
-
Listing Multiples: List the multiples of each denominator until you find the smallest common multiple.
- Multiples of 8: 8, 16, 24, 32, 40...
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27...
- The smallest common multiple is 24.
-
Prime Factorization: Break down each denominator into its prime factors. The LCD is the product of the highest powers of all prime factors present in either denominator.
- 8 = 2 x 2 x 2 = 2³
- 3 = 3
- LCD = 2³ x 3 = 24
Converting Fractions to a Common Denominator
Once we've found the LCD (24), we need to convert both fractions, 3/8 and 1/3, so they have this common denominator. To do this, we multiply the numerator and denominator of each fraction by the same number that will result in a denominator of 24.
-
For 3/8: To get a denominator of 24, we need to multiply 8 by 3 (because 8 x 3 = 24). Therefore, we multiply both the numerator and denominator by 3: (3 x 3) / (8 x 3) = 9/24
-
For 1/3: To get a denominator of 24, we need to multiply 3 by 8 (because 3 x 8 = 24). Therefore, we multiply both the numerator and denominator by 8: (1 x 8) / (3 x 8) = 8/24
Now both fractions have the same denominator, 24.
Performing the Addition
With both fractions having a common denominator, we can now add them:
9/24 + 8/24 = (9 + 8) / 24 = 17/24
Simplifying the Fraction (if necessary)
In this case, 17/24 is already in its simplest form. A fraction is in its simplest form when the greatest common divisor (GCD) of the numerator and denominator is 1. The GCD of 17 and 24 is 1, so we cannot simplify further.
Therefore, 3/8 + 1/3 = 17/24
Practical Applications and Real-World Examples
Understanding fraction addition isn't just about solving math problems; it has numerous real-world applications:
-
Cooking and Baking: Recipes often require fractions of ingredients. Adding fractions helps determine the total amount of an ingredient needed. For example, if a recipe calls for 1/2 cup of flour and 1/4 cup of sugar, you need to add the fractions to find the total amount of dry ingredients.
-
Construction and Measurement: Construction projects frequently involve precise measurements. Adding fractions is crucial when calculating total lengths, areas, or volumes.
-
Finance and Budgeting: Managing personal finances often requires working with fractions, especially when calculating portions of a budget or dealing with fractional shares of investments.
Expanding on Fraction Operations: Subtraction, Multiplication, and Division
While this article focused on addition, it's important to understand other fraction operations:
Subtraction: The process is similar to addition. Find the LCD, convert the fractions, then subtract the numerators. Keep the denominator the same.
Multiplication: Multiply the numerators together, then multiply the denominators together. Simplify the resulting fraction if necessary.
Division: To divide fractions, invert the second fraction (reciprocal) and then multiply.
Tips and Tricks for Mastering Fraction Addition
-
Practice Regularly: The more you practice, the more comfortable you'll become with the process. Start with simple problems and gradually increase the difficulty.
-
Visual Aids: Using visual aids like diagrams or fraction circles can make understanding fraction concepts easier.
-
Break Down Complex Problems: If you encounter a complex problem with multiple fractions, break it down into smaller, manageable steps.
-
Check Your Work: Always check your answer to ensure accuracy. You can do this by converting the fractions to decimals and then adding them. The decimal sum should be equivalent to the fraction sum.
Conclusion: Mastering Fractions for a Stronger Mathematical Foundation
Adding fractions, including the seemingly simple problem of 3/8 + 1/3, requires a systematic approach and a solid understanding of fundamental concepts. By mastering these concepts, you build a strong foundation for more advanced mathematical operations and effectively apply fraction arithmetic in various real-world scenarios. Remember to practice consistently and utilize various learning techniques to solidify your understanding. This will not only improve your mathematical skills but also enhance your problem-solving abilities in diverse fields. The ability to confidently work with fractions opens up a world of possibilities, from tackling complex equations to successfully navigating practical everyday situations.
Latest Posts
Latest Posts
-
What Is The Circumference Of A 12 Diameter Circle
May 14, 2025
-
82 Months Is How Many Years
May 14, 2025
-
What Is The Gcf Of 8 And 15
May 14, 2025
-
Cuantas Horas Son De 8 A 5
May 14, 2025
-
How Much Should I Sell Lemonade For
May 14, 2025
Related Post
Thank you for visiting our website which covers about What Is 3/8 + 1/3 In Fraction Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.