What Is 3 Percent Of 1200
Treneri
May 05, 2025 · 4 min read
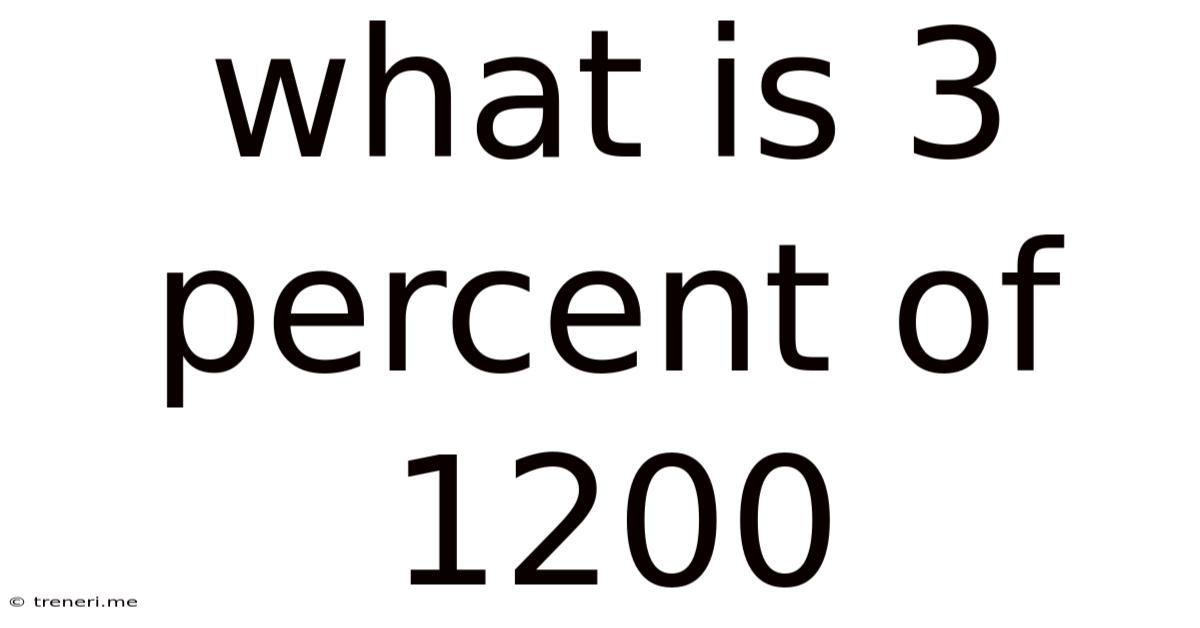
Table of Contents
What is 3 Percent of 1200? A Deep Dive into Percentage Calculations
Finding 3 percent of 1200 might seem like a simple calculation, but understanding the underlying principles of percentages is crucial for various aspects of life, from budgeting and finance to understanding statistics and data analysis. This article will not only provide the answer but also explore the different methods to calculate percentages, discuss practical applications, and delve into related concepts to build a solid understanding of this fundamental mathematical concept.
Understanding Percentages
Before diving into the calculation, let's solidify our understanding of percentages. A percentage is simply a fraction or ratio expressed as a part of 100. The symbol "%" represents "per hundred" or "out of 100." So, 3 percent (3%) means 3 out of 100, or 3/100 as a fraction, or 0.03 as a decimal.
Method 1: Using the Decimal Equivalent
This is arguably the most straightforward method. We convert the percentage into its decimal equivalent and then multiply it by the number.
Steps:
- Convert the percentage to a decimal: 3% = 3/100 = 0.03
- Multiply the decimal by the number: 0.03 * 1200 = 36
Therefore, 3 percent of 1200 is 36.
Method 2: Using the Fraction Equivalent
This method involves converting the percentage into a fraction and then performing the multiplication.
Steps:
- Convert the percentage to a fraction: 3% = 3/100
- Multiply the fraction by the number: (3/100) * 1200 = 3600/100 = 36
Again, the result is 36.
Method 3: Using Proportions
This method is particularly useful for understanding the underlying relationship between the percentage, the part, and the whole. We can set up a proportion:
- Part/Whole = Percentage/100
In our case:
- x/1200 = 3/100
To solve for x (which represents 3% of 1200), we cross-multiply:
- 100x = 3 * 1200
- 100x = 3600
- x = 3600/100
- x = 36
The answer, once more, is 36.
Practical Applications of Percentage Calculations
Understanding percentage calculations is vital in many real-world situations:
- Finance: Calculating interest on loans, savings accounts, or investments. Understanding discounts and sales tax. Analyzing financial statements and budgets.
- Retail: Determining discounts and markups on products. Calculating profit margins.
- Statistics: Interpreting data presented as percentages, such as survey results, demographics, or economic indicators.
- Science: Representing data in experiments, analyzing scientific studies and research findings.
- Everyday Life: Calculating tips at restaurants, understanding sales tax, or figuring out the percentage of a certain grade.
Advanced Percentage Calculations: Finding the Percentage One Number Represents of Another
Let's say we want to determine what percentage 36 represents of 1200. This calculation is frequently encountered in various scenarios, such as calculating grades or assessing proportions.
Steps:
- Divide the part by the whole: 36 / 1200 = 0.03
- Multiply the result by 100 to express it as a percentage: 0.03 * 100 = 3%
Therefore, 36 represents 3% of 1200.
Expanding on the Concept: Working with More Complex Percentages
While our example uses a simple 3%, the principles remain the same for more complex percentages, including those involving decimals or fractions. For example, finding 12.5% of 1200:
- Convert the percentage to a decimal: 12.5% = 12.5/100 = 0.125
- Multiply the decimal by the number: 0.125 * 1200 = 150
Thus, 12.5% of 1200 is 150.
Troubleshooting Common Errors in Percentage Calculations
Several common mistakes can lead to inaccurate results:
- Incorrect Decimal Conversion: A common mistake is misplacing the decimal point when converting percentages to decimals. Always remember that to convert a percentage to a decimal, divide the percentage by 100.
- Order of Operations: Ensure you follow the order of operations (PEMDAS/BODMAS) when performing calculations. Multiplication or division should be completed before addition or subtraction.
- Misunderstanding the Context: Carefully read the problem statement to ensure you understand which value is the whole and which is the part.
Conclusion: Mastering Percentage Calculations
Understanding percentages is a crucial life skill applicable in numerous contexts. While finding 3% of 1200 might seem basic, grasping the methods described here provides a strong foundation for tackling more complex percentage calculations. By mastering these methods and avoiding common errors, you can confidently approach any percentage-related problem. Remember to practice regularly to enhance your understanding and speed. The more you practice, the more intuitive percentage calculations will become. This skill will undoubtedly prove valuable in both personal and professional endeavors.
Latest Posts
Latest Posts
-
How Big Is A 10000 Sq Ft Lot
May 07, 2025
-
2 3 To The Second Power
May 07, 2025
-
How Much Concrete To Fill A Sonotube
May 07, 2025
-
How Many Km Is 1000 Miles
May 07, 2025
-
What Is 6 Percent Of 150
May 07, 2025
Related Post
Thank you for visiting our website which covers about What Is 3 Percent Of 1200 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.