What Is 3 Percent Of 200
Treneri
May 09, 2025 · 5 min read
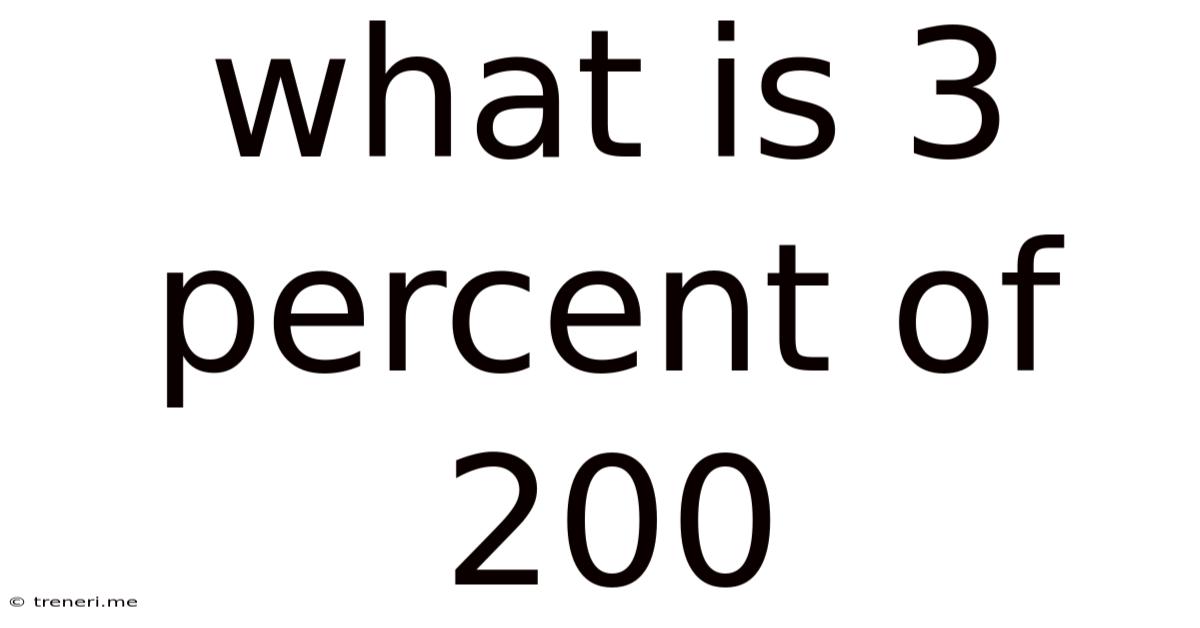
Table of Contents
What is 3 Percent of 200? A Deep Dive into Percentages and Their Applications
Finding 3 percent of 200 might seem like a simple arithmetic problem, but understanding the underlying concepts of percentages and their widespread applications unlocks a world of practical uses. This article will not only answer the question directly but also explore the various methods for calculating percentages, explain the significance of percentages in different fields, and delve into related concepts to provide a comprehensive understanding.
Calculating 3 Percent of 200: The Basics
The most straightforward way to calculate 3 percent of 200 is to convert the percentage to a decimal and then multiply. Remember that a percentage is simply a fraction out of 100. Therefore, 3 percent can be written as 3/100 or 0.03.
The calculation:
0.03 * 200 = 6
Therefore, 3 percent of 200 is 6.
Different Methods for Calculating Percentages
While the above method is the most efficient, understanding alternative approaches can enhance your comprehension of percentages and provide flexibility in different scenarios.
Method 2: Using Fractions
We can also express 3% as a fraction: 3/100. To find 3% of 200, we multiply:
(3/100) * 200 = 6
This method highlights the fractional nature of percentages.
Method 3: Proportionality
Percentages can be solved using proportions. We can set up a proportion:
3/100 = x/200
To solve for x (3% of 200), we cross-multiply:
100x = 3 * 200 100x = 600 x = 6
This method reinforces the proportional relationship inherent in percentages.
The Significance of Percentages in Everyday Life
Percentages are fundamental to numerous aspects of daily life, from personal finance to scientific analysis. Their ubiquitous nature stems from their ability to represent proportions in a clear and concise manner.
Personal Finance:
- Interest rates: Loans, savings accounts, and credit cards all involve interest rates expressed as percentages. Understanding percentage calculations is crucial for managing finances effectively and avoiding high-interest charges. For example, understanding how much interest will accrue on a loan or how much interest you will earn on savings.
- Discounts and Sales: Sales and discounts are commonly advertised as percentages. Quickly calculating these discounts helps make informed purchasing decisions.
- Taxes: Sales tax, income tax, and property tax are all calculated as percentages of a base amount. Knowing how to calculate these percentages is important for budgeting and financial planning.
- Tips and Gratuities: Calculating tips in restaurants usually involves determining a percentage of the bill.
Business and Economics:
- Profit margins: Businesses use percentages to calculate profit margins, which represent the percentage of revenue remaining after deducting costs. Analyzing profit margins helps businesses assess their financial health and profitability.
- Market share: Market share, representing a company's portion of the total market for a particular product or service, is usually expressed as a percentage. Analyzing market share helps companies understand their competitiveness and position within the market.
- Growth rates: Economic growth, population growth, and company revenue growth are often expressed as percentages. These percentages provide a concise way to track changes over time and make comparisons.
- Inflation and deflation: Inflation and deflation rates are expressed as percentages and significantly impact pricing, purchasing power, and economic planning.
Science and Statistics:
- Data analysis: Percentages are extensively used in statistical data analysis to represent proportions, frequencies, and changes in data. Analyzing data using percentages helps researchers draw conclusions and make informed decisions.
- Probability: Probability is often expressed as a percentage, representing the likelihood of an event occurring. This is fundamental to many areas including risk assessment and decision-making under uncertainty.
- Scientific experiments: Results from scientific experiments are often expressed as percentages to show the proportion of successful outcomes or the level of a certain substance present.
Healthcare:
- Drug efficacy: The effectiveness of medications and treatments is often represented as a percentage, indicating the rate of success.
- Disease prevalence: The percentage of a population affected by a specific disease is a crucial indicator of public health.
- Survival rates: Survival rates after medical treatments or surgeries are usually expressed as percentages, providing critical information for patients and healthcare providers.
Expanding the Concept: Beyond Simple Percentage Calculations
While calculating 3% of 200 is a straightforward exercise, the applications of percentages extend to more complex scenarios.
Calculating the Percentage Increase or Decrease:
Imagine a product that increased in price from $200 to $212. To calculate the percentage increase, we first find the difference: $212 - $200 = $12. Then, we divide this difference by the original price and multiply by 100: ($12/$200) * 100 = 6%. The price increased by 6%.
Similarly, if the price decreased from $200 to $194, the percentage decrease is calculated as (($200-$194)/$200)*100 = 3%.
Finding the Original Value:
Suppose you know that 3% of a number is 6. To find the original number, you can set up an equation:
0.03 * x = 6
Solving for x: x = 6 / 0.03 = 200
This demonstrates the reverse calculation—finding the base value when a percentage and its result are known.
Percentage Points vs. Percentage Change: A Crucial Distinction
It is important to note the difference between percentage points and percentage change. Percentage points refer to the simple difference between two percentages, while percentage change refers to the relative change expressed as a percentage.
For example, if the interest rate increases from 2% to 5%, the increase is 3 percentage points. However, the percentage change is calculated as ((5-2)/2) * 100 = 150%. This highlights the importance of carefully defining terminology when discussing percentage changes.
Conclusion: The Power of Percentage Understanding
Understanding percentages is not just about solving simple arithmetic problems. It's about grasping a fundamental concept that permeates various aspects of life, from personal finance to scientific research. Mastering percentage calculations empowers you to make informed decisions, interpret data effectively, and confidently navigate a world filled with numerical information. The ability to quickly and accurately calculate and interpret percentages is a valuable skill that enhances critical thinking and problem-solving capabilities across various fields. Beyond the simple calculation of 3% of 200, this article aims to illuminate the depth and breadth of percentage applications, showcasing its importance in numerous contexts. The power of percentage understanding extends far beyond the initial calculation; it unlocks a deeper comprehension of numerical relationships and data interpretation, thus making it a cornerstone of informed decision-making in our data-driven world.
Latest Posts
Latest Posts
-
Simplify The Following Union And Or Intersection
May 11, 2025
-
How Many Calories Burnt In 5km Run
May 11, 2025
-
What Is The Percent Change From 36 To 99
May 11, 2025
-
Cuanto Es 12 Pulgadas En Metros
May 11, 2025
-
What Is 5 Of One Million
May 11, 2025
Related Post
Thank you for visiting our website which covers about What Is 3 Percent Of 200 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.