What Is 3 Percent Of 80
Treneri
May 09, 2025 · 5 min read
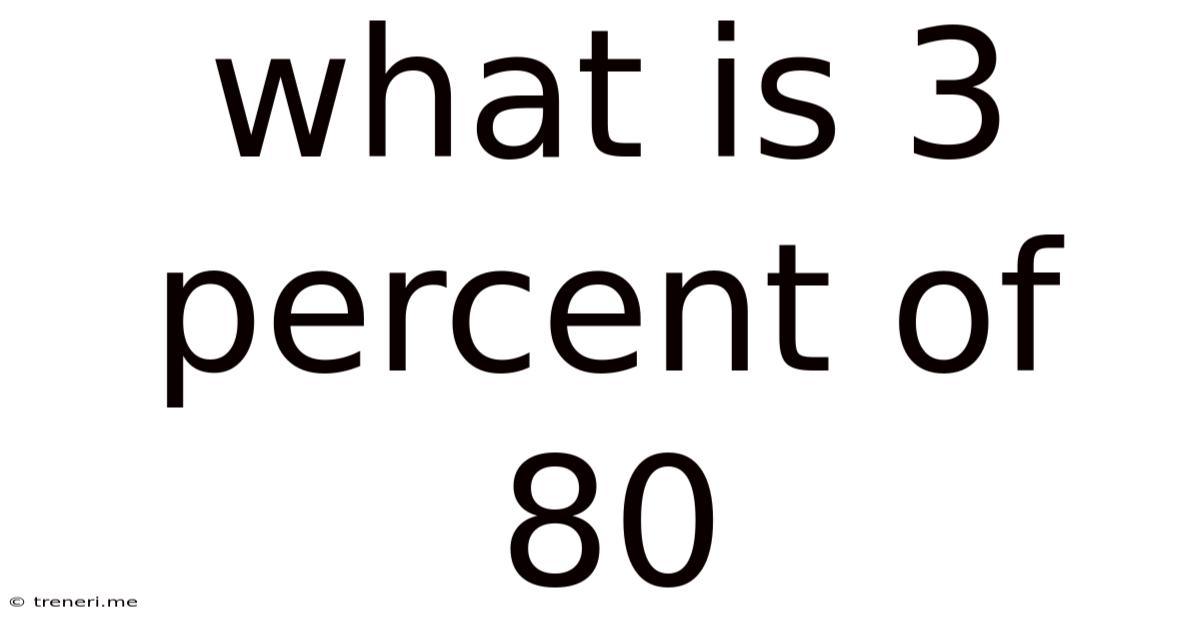
Table of Contents
What is 3 Percent of 80? A Deep Dive into Percentage Calculations
Finding 3 percent of 80 might seem like a simple task, but understanding the underlying principles of percentage calculations is crucial for various applications in daily life, from calculating discounts and taxes to understanding financial reports and statistical data. This article delves into the different methods for calculating 3% of 80, explores the concept of percentages in detail, and provides practical examples to solidify your understanding.
Understanding Percentages: The Foundation
A percentage is a fraction or a ratio expressed as a number out of 100. The term "percent" literally means "out of one hundred" (per centum in Latin). Therefore, 3% represents 3 parts out of 100, or 3/100 as a fraction, or 0.03 as a decimal. Understanding this fundamental concept is key to mastering percentage calculations.
Converting Percentages to Fractions and Decimals
Before tackling the calculation of 3% of 80, let's review the process of converting percentages to their fractional and decimal equivalents:
-
Percentage to Fraction: To convert a percentage to a fraction, simply write the percentage number as the numerator and 100 as the denominator. For example, 3% becomes 3/100. This fraction can then be simplified if necessary.
-
Percentage to Decimal: To convert a percentage to a decimal, divide the percentage number by 100. For 3%, this means dividing 3 by 100, resulting in 0.03. Alternatively, you can move the decimal point two places to the left.
Method 1: Using the Decimal Equivalent
This is arguably the most straightforward method for calculating 3% of 80. We'll leverage the decimal equivalent of 3%, which is 0.03.
-
Convert the percentage to a decimal: As established, 3% is equal to 0.03.
-
Multiply the decimal by the number: Multiply 0.03 by 80: 0.03 * 80 = 2.4
Therefore, 3% of 80 is 2.4.
This method is efficient and easily adaptable for various percentage calculations. It's particularly useful when working with calculators or spreadsheets.
Method 2: Using the Fractional Equivalent
This method utilizes the fractional representation of 3%, which is 3/100.
-
Convert the percentage to a fraction: 3% is equivalent to 3/100.
-
Multiply the fraction by the number: Multiply 3/100 by 80: (3/100) * 80 = 240/100
-
Simplify the fraction: 240/100 simplifies to 2.4 by dividing both the numerator and denominator by 100.
Therefore, 3% of 80 is 2.4. This method emphasizes the underlying fractional nature of percentages.
Method 3: Proportional Reasoning
This method uses the concept of ratios and proportions. It's a valuable method for understanding the relationship between percentages and the whole.
-
Set up a proportion: We can set up a proportion to represent the problem:
3/100 = x/80where 'x' represents 3% of 80. -
Cross-multiply: Cross-multiplying gives us:
100x = 3 * 80 -
Solve for x: This simplifies to
100x = 240. Dividing both sides by 100 gives usx = 2.4.
Therefore, 3% of 80 is 2.4. This method reinforces the proportional relationships inherent in percentage calculations.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is vital in numerous real-world scenarios:
-
Sales and Discounts: Calculating discounts on sale items. For instance, a 3% discount on an $80 item would be $2.40.
-
Taxes: Determining sales tax or other taxes on purchases. If the sales tax is 3%, the tax on an $80 purchase would be $2.40.
-
Interest Calculations: Calculating simple interest on loans or investments.
-
Financial Statements: Analyzing financial reports involving percentage changes in revenue, profit, or expenses.
-
Statistical Analysis: Interpreting statistical data presented as percentages. For example, understanding that 3% of a sample population possesses a certain characteristic.
-
Tip Calculation: Quickly figuring out a 3% tip on a restaurant bill of $80.
-
Commission Calculation: Determining the commission earned on sales, particularly in sales-based roles.
Expanding the Understanding: Beyond 3% of 80
While we've focused on calculating 3% of 80, the principles discussed apply to a wide range of percentage calculations. You can adapt these methods to find any percentage of any number. The key is to remember the fundamental concepts of converting percentages to fractions or decimals and applying the appropriate mathematical operations.
Troubleshooting Common Mistakes in Percentage Calculations
Several common mistakes can hinder accurate percentage calculations:
-
Incorrect Decimal Conversion: Failing to correctly convert a percentage to its decimal equivalent is a frequent error. Remember to divide the percentage by 100 or move the decimal point two places to the left.
-
Misplaced Decimal Point: Ensure the decimal point is correctly placed in the final answer.
-
Order of Operations: When dealing with multiple operations, adhere to the order of operations (PEMDAS/BODMAS) to avoid errors.
Advanced Percentage Calculations: Beyond the Basics
While calculating 3% of 80 is a fundamental calculation, there are more complex percentage problems. These could involve calculating percentage increases or decreases, finding the original value after a percentage change, or dealing with compound interest. These more advanced concepts build upon the foundational understanding of basic percentage calculations.
Conclusion: Mastering Percentage Calculations for Everyday Success
Calculating 3% of 80, though seemingly simple, provides a robust foundation for understanding and applying percentage calculations in numerous contexts. By grasping the methods outlined—using decimals, fractions, or proportional reasoning—you'll be equipped to handle a wide variety of percentage problems effectively. Remember that consistent practice and a clear understanding of the underlying principles are key to mastering percentage calculations and applying this essential skill to your everyday life. From managing personal finances to interpreting data in professional settings, the ability to confidently calculate percentages is a highly valuable asset.
Latest Posts
Latest Posts
-
What Fraction Is Equal To 9 12
May 09, 2025
-
How Many Cbm In A 40 Container
May 09, 2025
-
32 Feet Is How Many Inches
May 09, 2025
-
How Many Gallons Are In 360 Pints
May 09, 2025
-
Express The Interval As An Inequality
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Is 3 Percent Of 80 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.