What Is 3 To The Power Of 9
Treneri
May 09, 2025 · 5 min read
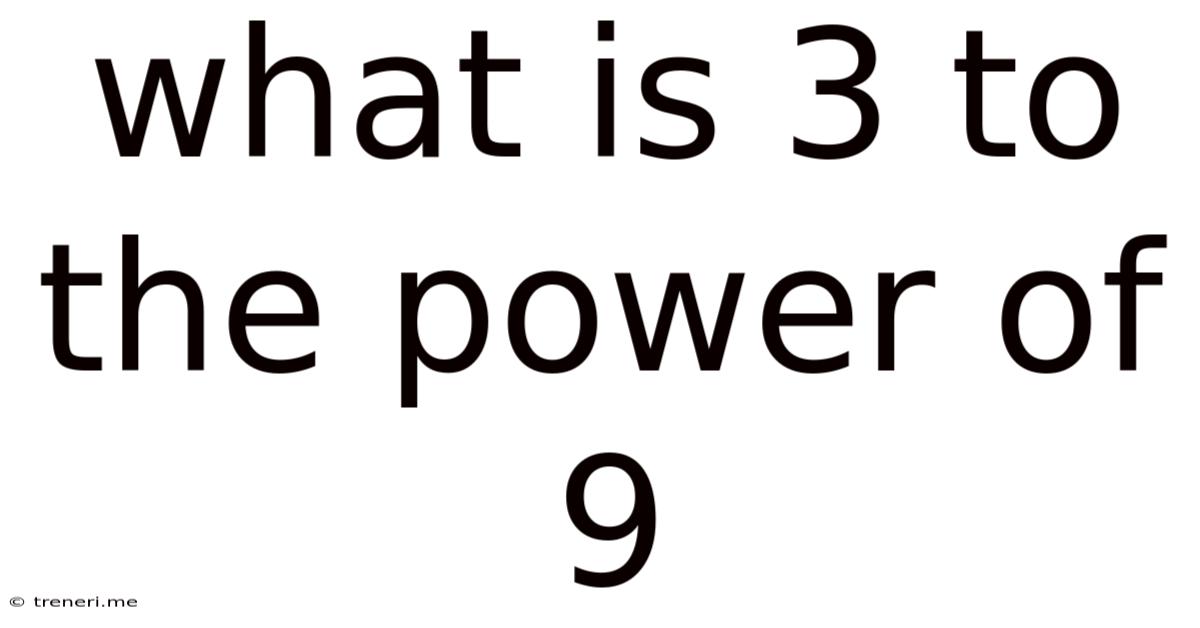
Table of Contents
What is 3 to the Power of 9? A Deep Dive into Exponentiation
The seemingly simple question, "What is 3 to the power of 9?" opens a door to a fascinating exploration of exponentiation, its applications, and the underlying mathematical principles. While the answer itself is readily calculable, understanding the why behind the calculation is where the true learning lies. This article delves deep into this seemingly simple problem, exploring its various facets and connecting it to broader mathematical concepts.
Understanding Exponentiation: Beyond Simple Multiplication
Before we tackle 3<sup>9</sup>, let's solidify our understanding of exponentiation. Exponentiation, represented by a base number raised to an exponent (or power), signifies repeated multiplication. In the expression a<sup>b</sup>, 'a' is the base, and 'b' is the exponent. This means 'a' is multiplied by itself 'b' times.
For example:
- 2<sup>3</sup> = 2 x 2 x 2 = 8 (The base 2 is multiplied by itself 3 times)
- 5<sup>2</sup> = 5 x 5 = 25 (The base 5 is multiplied by itself 2 times)
- 10<sup>1</sup> = 10 (The base 10 is multiplied by itself 1 time – simply itself)
- 1<sup>4</sup> = 1 x 1 x 1 x 1 = 1 (Any number raised to the power of 1 equals itself. Any number raised to the power of 0 equals 1, except for 0 itself)
Calculating 3 to the Power of 9
Now, let's address the main question: What is 3<sup>9</sup>? This means we need to multiply 3 by itself nine times:
3<sup>9</sup> = 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3
Manually calculating this can be tedious, but a calculator readily provides the answer:
3<sup>9</sup> = 19683
Methods for Calculating Exponents
While a calculator offers the quickest solution, understanding different approaches enriches our mathematical understanding. Let's explore some alternative methods:
1. Step-by-Step Multiplication:
This is the most straightforward approach, as demonstrated above. It's ideal for smaller exponents but becomes cumbersome for larger ones.
2. Using Properties of Exponents:
Mathematical properties of exponents can simplify calculations. For instance:
-
a<sup>m</sup> x a<sup>n</sup> = a<sup>(m+n)</sup>: This allows us to combine exponents when multiplying numbers with the same base.
-
(a<sup>m</sup>)<sup>n</sup> = a<sup>(m x n)</sup>: This allows us to simplify expressions with exponents raised to another exponent.
For 3<sup>9</sup>, we could break it down strategically. We can express it as:
(3<sup>3</sup>)<sup>3</sup> = 27<sup>3</sup> = 27 x 27 x 27 = 19683
This method uses the second property of exponents, making the calculation less daunting.
3. Using Logarithms:
Logarithms are the inverse of exponents. If we know the logarithm of a number, we can find its exponent. However, for a simple calculation like 3<sup>9</sup>, using logarithms would be overkill and more complex than direct calculation. Logarithms are more useful when dealing with incredibly large numbers or solving equations involving exponents.
Applications of Exponentiation
Exponentiation is not just a mathematical curiosity; it has far-reaching applications across various fields:
1. Compound Interest:
In finance, compound interest calculations heavily rely on exponentiation. The formula A = P(1 + r/n)^(nt) utilizes exponentiation to determine the future value (A) of an investment based on the principal amount (P), interest rate (r), compounding periods (n), and time (t).
2. Population Growth:
In biology and ecology, exponential functions model population growth (under ideal conditions). Factors like birth rate, death rate, and migration rates influence the growth rate which is represented exponentially over time.
3. Radioactive Decay:
The decay of radioactive isotopes follows an exponential pattern. The formula used to model this decay involves an exponential term determining the remaining amount of the isotope after a certain period.
4. Computer Science:
Exponentiation is fundamental in computer science, particularly in algorithms and data structures. The time complexity of certain algorithms is expressed using exponential notation. This helps analyze the efficiency of these algorithms as input size increases.
5. Physics and Engineering:
Exponential functions appear in various physics and engineering applications, modeling phenomena like exponential attenuation of signals, heat transfer, and the behavior of certain electronic components.
Expanding on the Concept: Beyond the Basics
Let's extend our understanding beyond the specific calculation of 3<sup>9</sup>. We can explore related concepts and delve deeper into the world of exponentials:
Negative Exponents:
When the exponent is negative, it represents the reciprocal of the base raised to the positive exponent. For example:
3<sup>-2</sup> = 1 / 3<sup>2</sup> = 1/9
Fractional Exponents:
Fractional exponents represent roots. For example:
3<sup>1/2</sup> = √3 (the square root of 3) 3<sup>1/3</sup> = ∛3 (the cube root of 3)
Complex Exponents:
Exponentiation can even extend to complex numbers, where the base and/or exponent can be complex numbers themselves. This is a more advanced topic involving Euler's formula and complex analysis.
Conclusion: The Power of Understanding
While the answer to "What is 3 to the power of 9?" is simply 19683, the journey to arrive at that answer and the exploration of the broader concepts surrounding exponentiation provide a significantly richer understanding of mathematics and its applications. Understanding the properties of exponents and their role in various fields highlights the power and versatility of this fundamental mathematical operation. From compound interest to radioactive decay, exponential functions play a crucial role in modeling real-world phenomena, highlighting the importance of grasping this seemingly simple yet powerful concept. This exploration goes beyond a simple calculation, transforming it into an insightful journey into the heart of mathematical principles and their practical relevance.
Latest Posts
Latest Posts
-
What Is The Lcm Of 4 6 10
May 09, 2025
-
Two Months Is How Many Days
May 09, 2025
-
How Many Gallons In 15x30 Pool
May 09, 2025
-
Commission On 20 Million Dollar House
May 09, 2025
-
What Is 3 To The Fifth Power
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Is 3 To The Power Of 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.