What Is 30/40 As A Percentage
Treneri
May 15, 2025 · 4 min read
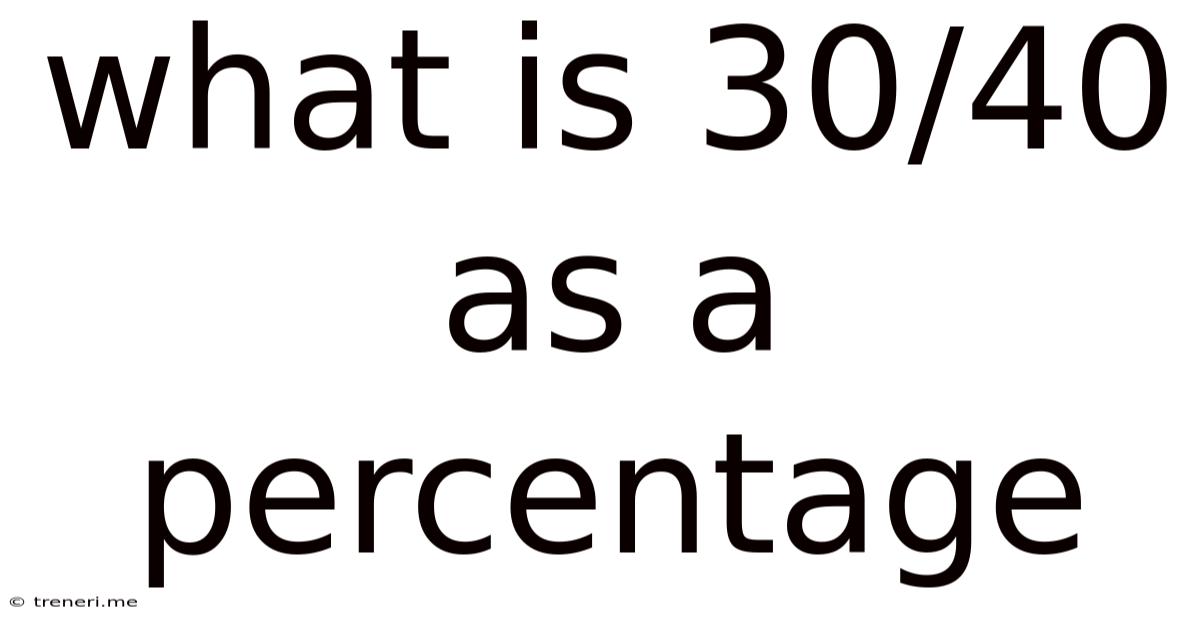
Table of Contents
What is 30/40 as a Percentage? A Comprehensive Guide
Understanding fractions and their percentage equivalents is a fundamental skill in various aspects of life, from everyday calculations to complex financial analyses. This comprehensive guide will delve deep into determining the percentage representation of the fraction 30/40, exploring the underlying concepts and providing practical applications. We'll cover multiple methods for calculating this, clarifying common misconceptions, and showcasing how this knowledge can be applied in real-world scenarios.
Understanding Fractions and Percentages
Before we dive into calculating 30/40 as a percentage, let's refresh our understanding of fractions and percentages.
Fractions: A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). In our case, 30/40, 30 is the numerator and 40 is the denominator. This means 30 out of 40 parts of a whole.
Percentages: A percentage is a way of expressing a fraction as a portion of 100. The symbol "%" represents "per hundred" or "out of 100". Percentages are frequently used to represent proportions, rates, or changes.
Method 1: Simplifying the Fraction
The most straightforward method to convert 30/40 to a percentage involves simplifying the fraction first. This makes the subsequent calculation easier.
Step 1: Find the Greatest Common Divisor (GCD)
The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder. For 30 and 40, the GCD is 10.
Step 2: Divide Both Numerator and Denominator by the GCD
Dividing both 30 and 40 by 10, we get:
30 ÷ 10 = 3 40 ÷ 10 = 4
This simplifies the fraction 30/40 to 3/4.
Step 3: Convert the Simplified Fraction to a Percentage
To convert a fraction to a percentage, we multiply the fraction by 100%:
(3/4) * 100% = 75%
Therefore, 30/40 is equal to 75%.
Method 2: Direct Conversion using Decimal
This method bypasses fraction simplification and directly converts the fraction to a decimal before expressing it as a percentage.
Step 1: Divide the Numerator by the Denominator
Divide the numerator (30) by the denominator (40):
30 ÷ 40 = 0.75
Step 2: Multiply the Decimal by 100%
Multiply the resulting decimal (0.75) by 100%:
0.75 * 100% = 75%
Again, we arrive at the conclusion that 30/40 is equivalent to 75%.
Method 3: Using Proportions
This method uses the concept of proportions to solve the problem. We can set up a proportion to find the equivalent percentage.
Step 1: Set up a Proportion
We can set up a proportion as follows:
30/40 = x/100
Where 'x' represents the percentage we want to find.
Step 2: Cross-Multiply
Cross-multiply the proportion:
30 * 100 = 40 * x
3000 = 40x
Step 3: Solve for x
Divide both sides by 40 to solve for x:
x = 3000 ÷ 40
x = 75
Therefore, 30/40 is equivalent to 75%.
Understanding the Result: 75%
The result, 75%, signifies that 30 represents 75% of 40. This means that if you divide 40 into 100 equal parts, 30 would occupy 75 of those parts.
Real-World Applications of Percentage Calculations
Understanding percentage calculations, as demonstrated by converting 30/40 to 75%, is crucial in various real-world applications:
-
Financial Calculations: Calculating interest rates, discounts, taxes, profit margins, and investment returns all rely heavily on percentage calculations. For example, a 75% discount on a $100 item would mean a reduction of $75.
-
Academic Performance: Grading systems often use percentages to represent student performance. A score of 30 out of 40 on a test equates to a 75% grade.
-
Data Analysis: Percentages are essential for interpreting and visualizing data. They provide a standardized way to compare proportions across different datasets. For instance, if a survey shows 30 out of 40 respondents prefer a certain product, it represents a 75% preference rate.
-
Statistical Analysis: Percentages are fundamental in statistical analysis for calculating probabilities, confidence intervals, and other statistical measures.
-
Everyday Life: Calculating tips, understanding sale prices, and determining the percentage of ingredients in a recipe all involve percentage calculations.
Common Mistakes to Avoid
While the conversion of 30/40 to a percentage is relatively straightforward, some common mistakes can occur:
-
Incorrect Simplification: Failing to simplify the fraction before converting to a percentage can lead to more complex calculations and potential errors.
-
Incorrect Decimal Placement: When converting the decimal to a percentage, ensure the decimal point is moved two places to the right.
-
Misunderstanding the Concept: A fundamental misunderstanding of fractions and percentages can lead to incorrect interpretations and applications.
-
Calculation Errors: Simple mathematical errors during the calculation process should be avoided through careful attention and double-checking.
Conclusion
Converting 30/40 to a percentage is a fundamental mathematical skill with broad applications across various fields. By understanding the different methods—simplifying the fraction, direct decimal conversion, and using proportions—one can confidently and accurately convert fractions to percentages. Mastering this skill equips you with essential tools for navigating everyday situations and tackling more complex problems involving proportions and ratios. Remember to always double-check your calculations and understand the context of the percentage to avoid common mistakes and ensure accurate results. The ability to easily translate fractions into percentages enhances your analytical skills and allows you to interpret and utilize data effectively in numerous real-world applications.
Latest Posts
Latest Posts
-
88 83 Is What Percent Of 21
May 15, 2025
-
Cuantas Semanas Tiene Un Ano De 365 Dias
May 15, 2025
-
How Many Ounce In A Kilogram
May 15, 2025
-
How Many Cubic Feet Is 55 Quarts Of Potting Soil
May 15, 2025
-
What Is The Gcf For 18 And 32
May 15, 2025
Related Post
Thank you for visiting our website which covers about What Is 30/40 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.