What Is 35 8 As A Mixed Number
Treneri
May 10, 2025 · 4 min read
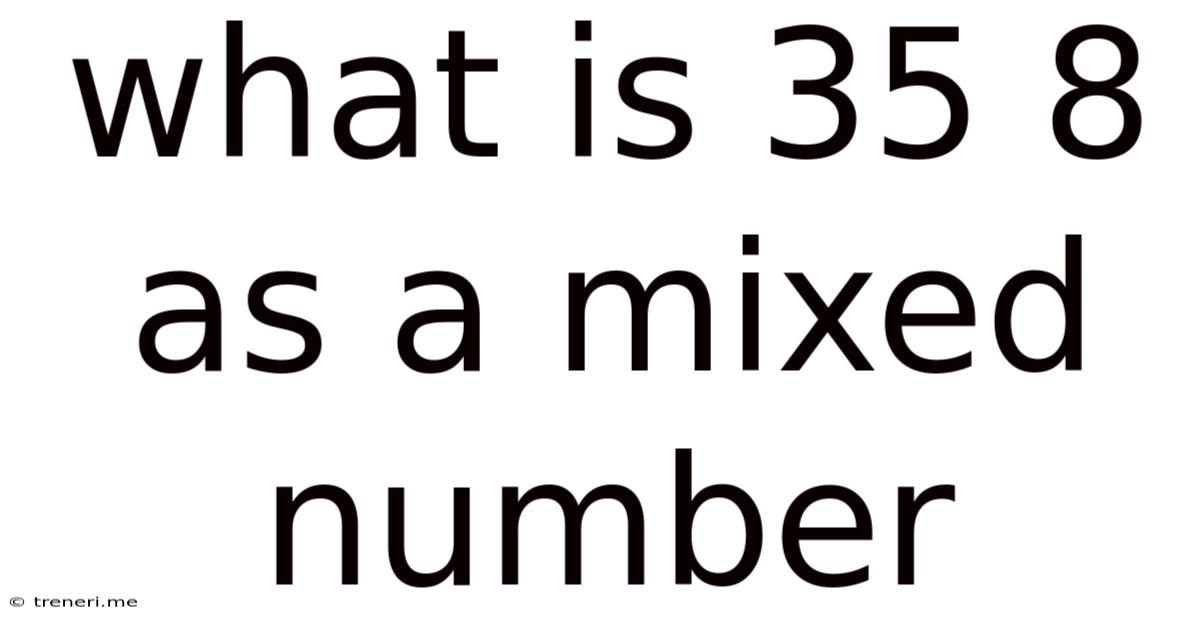
Table of Contents
What is 35/8 as a Mixed Number? A Comprehensive Guide
Understanding how to convert improper fractions, like 35/8, into mixed numbers is a fundamental skill in mathematics. This comprehensive guide will not only show you how to convert 35/8 into a mixed number but will also delve into the underlying principles, provide you with various methods, and equip you with the knowledge to tackle similar problems with confidence.
Understanding Fractions: A Quick Refresher
Before we dive into the conversion, let's refresh our understanding of fractions. A fraction represents a part of a whole. It consists of two parts:
- Numerator: The top number, indicating the number of parts you have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
An improper fraction is a fraction where the numerator is greater than or equal to the denominator (e.g., 35/8). A mixed number combines a whole number and a proper fraction (e.g., 4 3/8). A proper fraction has a numerator smaller than the denominator (e.g., 3/8).
Converting 35/8 to a Mixed Number: The Standard Method
The most common method for converting an improper fraction to a mixed number involves division. Here's how to convert 35/8:
-
Divide the numerator by the denominator: Divide 35 by 8.
35 ÷ 8 = 4 with a remainder of 3.
-
The quotient becomes the whole number: The quotient (4) becomes the whole number part of the mixed number.
-
The remainder becomes the numerator: The remainder (3) becomes the numerator of the fractional part.
-
The denominator remains the same: The denominator (8) remains unchanged.
Therefore, 35/8 as a mixed number is 4 3/8.
Visualizing the Conversion: A Practical Approach
Imagine you have 35 pieces of pizza, and each pizza is cut into 8 slices. To find out how many whole pizzas you have and how many slices are left over, you can use the division method explained above. You'd have 4 whole pizzas (4 x 8 = 32 slices) and 3 slices left over. This translates to 4 3/8 pizzas. This visual representation helps solidify the understanding of the conversion process.
Alternative Methods: Exploring Different Approaches
While the standard division method is the most straightforward, let's explore a couple of alternative methods that might enhance your understanding:
Method 2: Repeated Subtraction
This method involves repeatedly subtracting the denominator from the numerator until you reach a number less than the denominator. Let's apply this to 35/8:
- Subtract the denominator (8) from the numerator (35): 35 - 8 = 27
- Repeat the subtraction: 27 - 8 = 19; 19 - 8 = 11; 11 - 8 = 3
- Count the number of subtractions: We subtracted 8 four times. This is our whole number.
- The remaining number is the new numerator: The remaining number (3) is our new numerator.
- The denominator stays the same: The denominator remains 8.
This again results in the mixed number 4 3/8.
Method 3: Using Equivalent Fractions
This less common method involves finding an equivalent fraction with a numerator that's a multiple of the denominator. While less practical for larger numbers, it's a valuable exercise in understanding fraction equivalence. It's difficult to directly apply this method to 35/8 intuitively, as finding an equivalent fraction with a numerator easily divisible by 8 requires some trial and error. However, the understanding behind it reinforces the concept of fraction equivalence.
Beyond 35/8: Applying the Knowledge to Other Improper Fractions
The methods discussed above can be applied to any improper fraction. Let's try another example: Convert 22/5 to a mixed number.
- Divide the numerator by the denominator: 22 ÷ 5 = 4 with a remainder of 2.
- The quotient is the whole number: The whole number is 4.
- The remainder is the new numerator: The new numerator is 2.
- The denominator remains the same: The denominator is 5.
Therefore, 22/5 as a mixed number is 4 2/5.
Simplifying Mixed Numbers: A Final Step
Sometimes, the fractional part of a mixed number can be simplified. For example, if we had obtained 4 6/12, we could simplify the fraction 6/12 to 1/2, resulting in the simplified mixed number 4 1/2. Always check if the fractional part can be simplified to its lowest terms. In the case of 4 3/8, the fraction 3/8 is already in its simplest form.
Conclusion: Mastering Fraction Conversions
Converting improper fractions to mixed numbers is a crucial skill in mathematics. Understanding the underlying principles, combined with practice using the different methods, will solidify your comprehension and enable you to confidently tackle such problems. Remember, the core concept revolves around dividing the numerator by the denominator and expressing the result as a whole number and a remaining fraction. This guide provides you with not just the answer but the knowledge to confidently handle future fraction conversion challenges. Practice regularly and you'll quickly master this essential mathematical skill.
Latest Posts
Latest Posts
-
How Many Hours Is 68 Days
May 10, 2025
-
Calculate The Freezing Point Of The Solution
May 10, 2025
-
What Is 4 5 Equivalent To
May 10, 2025
-
How To Find Cubic Feet Of A Circle
May 10, 2025
-
Cuanto Es 6 Kilogramos En Libras
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Is 35 8 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.