What Is 4/2 In Simplest Form
Treneri
May 11, 2025 · 5 min read
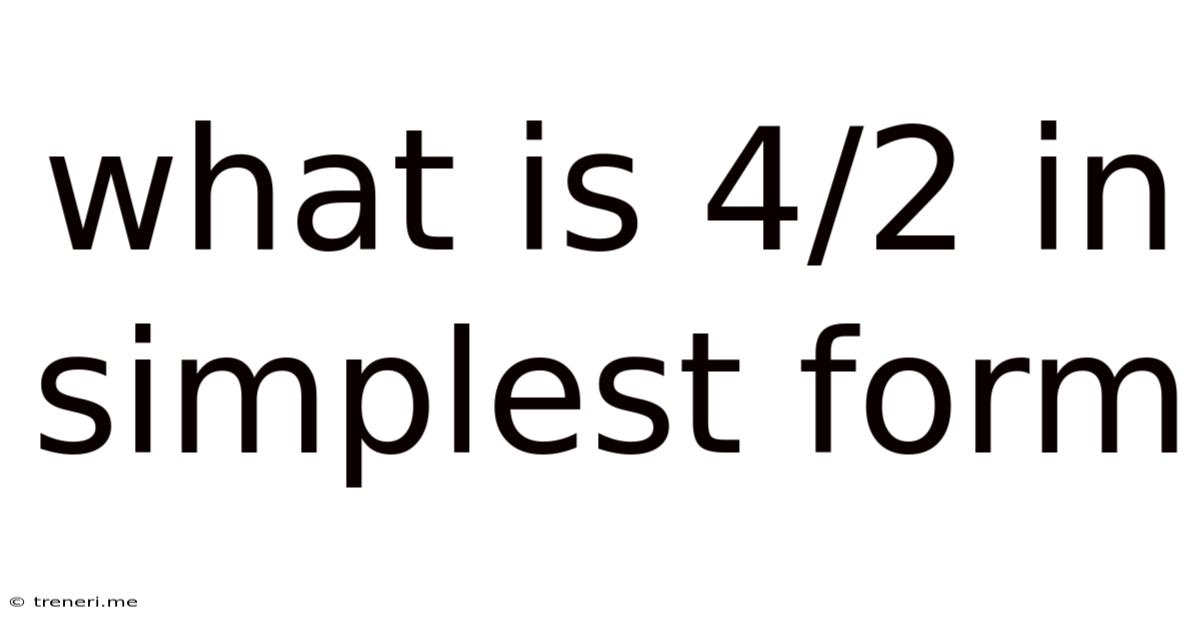
Table of Contents
What is 4/2 in Simplest Form? A Deep Dive into Fraction Simplification
The seemingly simple question, "What is 4/2 in simplest form?", opens a door to a fundamental concept in mathematics: fraction simplification. While the answer itself is straightforward, understanding the why behind the process is crucial for mastering more complex fraction operations and algebraic manipulations later on. This article will not only answer the question but delve deep into the principles of fraction simplification, providing you with a robust understanding of the subject.
Understanding Fractions: Parts of a Whole
Before tackling the simplification of 4/2, let's revisit the basic definition of a fraction. A fraction represents a part of a whole. It's written in the form a/b, where:
- a is the numerator: This represents the number of parts we have.
- b is the denominator: This represents the total number of equal parts the whole is divided into.
For example, in the fraction 3/4, the numerator (3) indicates we have 3 parts, and the denominator (4) indicates the whole is divided into 4 equal parts.
Simplifying Fractions: Finding the Lowest Terms
Simplifying a fraction means expressing it in its simplest form, where the numerator and denominator have no common factors other than 1. This process is also known as reducing a fraction to its lowest terms. The simplified fraction represents the same value as the original fraction but with smaller numbers, making it easier to understand and work with.
The key to simplifying fractions lies in finding the greatest common divisor (GCD) or highest common factor (HCF) of the numerator and the denominator. The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
Methods for Finding the Greatest Common Divisor (GCD)
Several methods can be used to find the GCD:
-
Listing Factors: This method involves listing all the factors of both the numerator and the denominator and identifying the largest factor they share. While effective for smaller numbers, it becomes cumbersome for larger numbers.
-
Prime Factorization: This is a more efficient method, especially for larger numbers. It involves breaking down both the numerator and the denominator into their prime factors. The GCD is then the product of the common prime factors raised to the lowest power.
-
Euclidean Algorithm: This is an algorithmic approach that efficiently finds the GCD of two numbers using successive division. It's particularly useful for larger numbers where listing factors or prime factorization becomes tedious.
Solving 4/2: A Step-by-Step Approach
Now, let's apply these concepts to the fraction 4/2.
1. Identify the Numerator and Denominator:
In the fraction 4/2, the numerator is 4, and the denominator is 2.
2. Find the Greatest Common Divisor (GCD):
Let's use the prime factorization method:
- Prime factorization of 4: 2 x 2
- Prime factorization of 2: 2
The common prime factor is 2. Therefore, the GCD of 4 and 2 is 2.
3. Divide the Numerator and Denominator by the GCD:
Divide both the numerator and the denominator by the GCD (2):
4 ÷ 2 = 2 2 ÷ 2 = 1
4. The Simplest Form:
The simplified fraction is 2/1.
5. Expressing as a Whole Number:
Since the denominator is 1, this fraction can be expressed as a whole number: 2.
Therefore, 4/2 in simplest form is 2.
Beyond 4/2: Practical Applications and Further Exploration
The simplification of fractions is not just an abstract mathematical concept; it's a fundamental skill with wide-ranging applications:
-
Everyday Calculations: Whether you're sharing a pizza, measuring ingredients for a recipe, or calculating proportions, simplifying fractions makes the calculations clearer and more efficient.
-
Algebra and Higher Mathematics: The ability to simplify fractions is essential for solving equations, simplifying algebraic expressions, and working with more complex mathematical concepts like calculus.
-
Data Analysis and Statistics: Fractions often appear in data analysis and statistics, and simplifying them is crucial for interpreting results accurately.
-
Engineering and Construction: Accurate measurements and proportions are critical in engineering and construction, and simplifying fractions ensures precise calculations.
More Examples of Fraction Simplification
Let's explore a few more examples to solidify our understanding:
- 6/9: The GCD of 6 and 9 is 3. Dividing both by 3 gives 2/3.
- 12/18: The GCD of 12 and 18 is 6. Dividing both by 6 gives 2/3.
- 25/100: The GCD of 25 and 100 is 25. Dividing both by 25 gives 1/4.
- 15/45: The GCD of 15 and 45 is 15. Dividing both by 15 gives 1/3.
- 108/144: The GCD of 108 and 144 is 36. Dividing both by 36 gives 3/4
Understanding Equivalent Fractions
Simplifying a fraction doesn't change its value; it simply represents the same value in a more concise form. Fractions that represent the same value are called equivalent fractions. For example, 4/2, 2/1, and 2 are all equivalent fractions. They all represent the same quantity.
Common Mistakes to Avoid
When simplifying fractions, several common mistakes can occur:
-
Incorrectly finding the GCD: Failing to identify the largest common factor will result in an incomplete simplification.
-
Dividing only the numerator or denominator: Remember that you must divide both the numerator and denominator by the GCD.
-
Forgetting to express as a whole number: If the denominator becomes 1 after simplification, the fraction is equivalent to the numerator as a whole number.
Conclusion: Mastering Fraction Simplification
The ability to simplify fractions is a fundamental skill that underpins many mathematical operations. By understanding the concepts of fractions, greatest common divisors, and equivalent fractions, you can confidently simplify fractions of any size, paving the way for success in more advanced mathematical studies and real-world applications. Remember to practice regularly to solidify your understanding and build confidence in your ability to work with fractions. The seemingly simple question of "What is 4/2 in simplest form?" opens a world of mathematical possibilities. Mastering this skill will equip you with a valuable tool for tackling more complex mathematical challenges in the future.
Latest Posts
Latest Posts
-
How Do You Find The Area Of Regular Polygons
May 12, 2025
-
What Is The Reciprocal Of 13
May 12, 2025
-
What Percentage Is 20 Out Of 24
May 12, 2025
-
How Much Is A 70 Percent Grade
May 12, 2025
-
An Inch Of Rain Is Equivalent To How Much Snow
May 12, 2025
Related Post
Thank you for visiting our website which covers about What Is 4/2 In Simplest Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.