What Is 4.3 As A Fraction
Treneri
May 13, 2025 · 5 min read
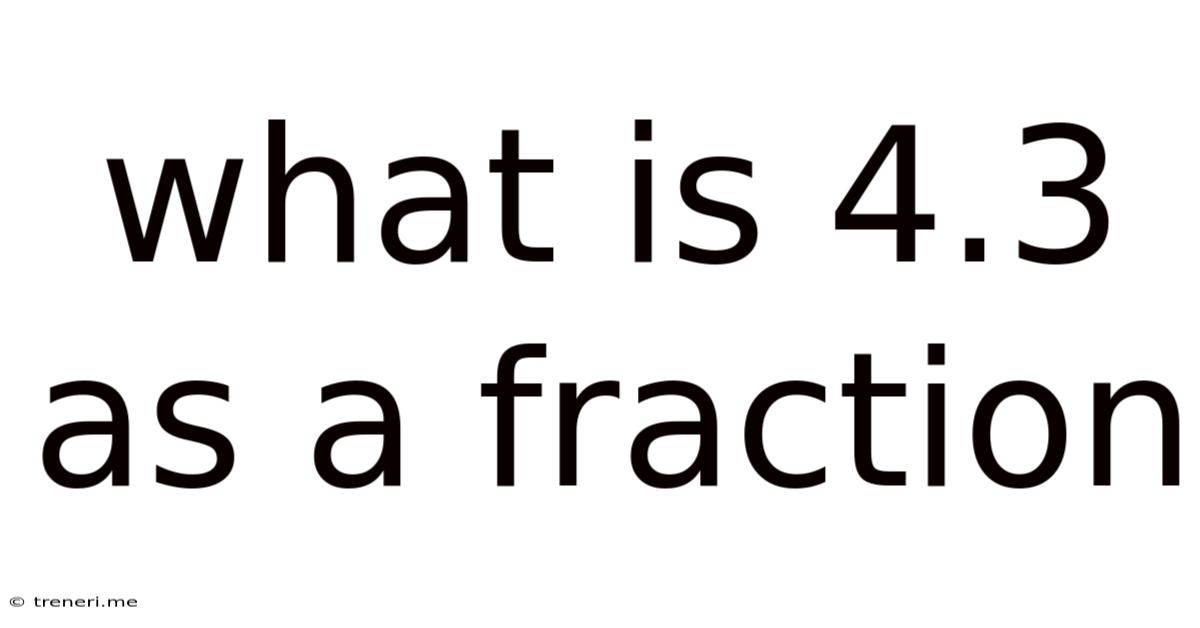
Table of Contents
What is 4.3 as a Fraction? A Comprehensive Guide
Understanding how to convert decimals to fractions is a fundamental skill in mathematics. This comprehensive guide will delve deep into the process of converting the decimal 4.3 into its fractional equivalent, exploring various methods and providing a solid foundation for similar conversions. We'll also discuss the importance of understanding decimal-to-fraction conversions in various fields and applications.
Understanding Decimals and Fractions
Before we dive into the conversion, let's refresh our understanding of decimals and fractions.
Decimals: Decimals represent numbers that are not whole numbers. They are written with a decimal point separating the whole number part from the fractional part. The digits to the right of the decimal point represent fractions of a power of 10 (tenths, hundredths, thousandths, and so on).
Fractions: Fractions represent parts of a whole. They are written as a ratio of two numbers, the numerator (top number) and the denominator (bottom number). The denominator indicates the number of equal parts the whole is divided into, and the numerator indicates how many of those parts are being considered.
Converting 4.3 to a Fraction: The Step-by-Step Process
The conversion of 4.3 to a fraction involves several straightforward steps:
Step 1: Identify the Whole Number and Decimal Part
The decimal 4.3 has a whole number part (4) and a decimal part (.3). This separation is crucial for the conversion process.
Step 2: Express the Decimal Part as a Fraction
The decimal part, .3, represents three-tenths. Therefore, we can express it as the fraction 3/10. Notice that the number of digits after the decimal point dictates the denominator. One digit after the decimal point means a denominator of 10, two digits would be 100, three digits would be 1000, and so on.
Step 3: Convert the Whole Number to an Improper Fraction (Optional but Recommended)
While not strictly necessary for the initial conversion, expressing the whole number as a fraction with the same denominator as the decimal part simplifies the next step. We can rewrite 4 as 40/10.
Step 4: Combine the Fractions
Now we can add the two fractions together: 40/10 + 3/10 = 43/10
Step 5: Simplify the Fraction (If Possible)
In this case, the fraction 43/10 is already in its simplest form. A fraction is simplified when the numerator and denominator share no common factors other than 1. If there were a common factor, we would divide both the numerator and the denominator by that factor to simplify the fraction.
Therefore, 4.3 as a fraction is 43/10.
Alternative Methods for Decimal-to-Fraction Conversion
While the above method is the most straightforward for simple decimals, other methods can be employed for more complex decimal conversions.
Method 2: Using the Place Value System
This method directly utilizes the place value of the digits in the decimal. For example, in 4.3, the '3' is in the tenths place, meaning it represents 3/10. The '4' is in the ones place, representing 4. Thus, combining these gives 4 + 3/10 = 43/10. This approach reinforces the understanding of decimal place values.
Method 3: Multiplying by a Power of 10
Another approach involves multiplying the decimal by a power of 10 to eliminate the decimal point. For 4.3, we multiply by 10: 4.3 * 10 = 43. This then becomes the numerator of the fraction. The denominator is the power of 10 used in the multiplication, which is 10 in this case. This gives us 43/10. This method is particularly useful for recurring decimals.
Applications of Decimal-to-Fraction Conversions
The ability to convert decimals to fractions is crucial in various fields:
Engineering and Design
Engineers and designers often work with precise measurements. Converting decimals to fractions allows for greater accuracy and facilitates calculations involving fractional dimensions.
Cooking and Baking
Recipes often use fractions for ingredient measurements. Being able to convert decimal measurements from electronic scales to fractional representations ensures consistency and accuracy in the final product.
Finance and Accounting
Financial calculations often involve fractional amounts. Converting decimals to fractions can simplify calculations and improve accuracy in financial reporting.
Computer Science
While computers work primarily with decimal representation, understanding the underlying fractional representation is critical for certain algorithms and data structures. The concept is fundamental in computer graphics and image processing.
Science and Research
Data analysis in scientific research frequently involves both decimal and fractional representations. Converting between the two ensures consistency and facilitates calculations and data interpretation.
Further Exploration: Converting More Complex Decimals
The techniques described above can be extended to convert more complex decimals, including those with multiple digits after the decimal point and recurring decimals. For example:
- 4.37: This would be converted to 437/100.
- 4.333... (recurring): This requires a slightly different approach and is best explained by considering the concept of geometric series.
The key to success lies in understanding the underlying principles of decimal representation and fractional equivalence.
Conclusion: Mastering Decimal-to-Fraction Conversions
Converting decimals to fractions is a fundamental mathematical skill with broad applications. By understanding the various methods and practicing the conversions, you will not only improve your mathematical abilities but also enhance your proficiency in diverse fields requiring numerical precision and accuracy. The ability to confidently convert decimals to fractions strengthens your problem-solving skills and provides a deeper comprehension of numerical representation. Remember that consistent practice and a solid understanding of the underlying concepts are key to mastering this essential skill. The conversion of 4.3 to 43/10 serves as a simple yet illustrative example of a broader, valuable mathematical capability.
Latest Posts
Latest Posts
-
Find The Difference Between 303 And 184
May 13, 2025
-
How To Find The Length Indicated
May 13, 2025
-
What Is The Factor Of 71
May 13, 2025
-
31 Km To Miles Per Hour
May 13, 2025
-
What Size Rug For 10x12 Room
May 13, 2025
Related Post
Thank you for visiting our website which covers about What Is 4.3 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.