What Is 4 3 Divided By 5 3
Treneri
May 10, 2025 · 4 min read
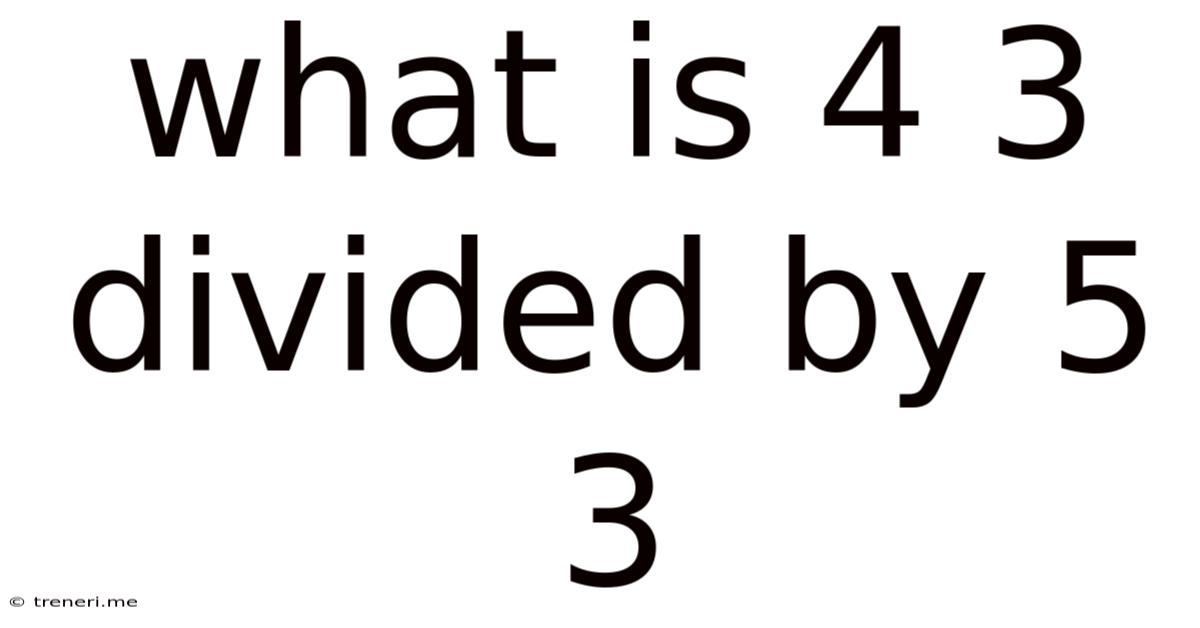
Table of Contents
Decoding the Enigma: What is 4³ Divided by 5³? A Deep Dive into Cubic Relationships
The seemingly simple question, "What is 4³ divided by 5³?", opens a door to a fascinating exploration of exponents, fractions, and the fundamental principles of mathematics. While a calculator can provide a quick numerical answer, understanding the underlying concepts provides a far richer understanding and empowers you to tackle similar problems with confidence. This comprehensive guide will not only solve the problem but also illuminate the broader mathematical principles at play.
Understanding Exponents and Cubes
Before diving into the division, let's solidify our understanding of exponents, specifically cubes. An exponent, or power, indicates how many times a number (the base) is multiplied by itself. In the case of cubes (represented by the exponent ³), the base number is multiplied by itself three times.
- 4³ (4 cubed) = 4 x 4 x 4 = 64
- 5³ (5 cubed) = 5 x 5 x 5 = 125
These calculations form the foundation of our problem. We're essentially dealing with the fraction 64/125.
Performing the Division: A Step-by-Step Approach
Now, let's tackle the division: 4³ / 5³. This translates to 64 / 125. We can approach this division in several ways:
1. Long Division: This traditional method involves manually dividing 64 by 125. While effective, it can be time-consuming for larger numbers. The result is a decimal value.
2. Using a Calculator: The simplest and quickest approach involves using a calculator. Simply enter 64 ÷ 125 and you'll obtain the decimal equivalent.
3. Simplifying the Fraction: Before resorting to decimal form, let's examine if the fraction can be simplified. In this case, 64 and 125 share no common factors other than 1. Therefore, the fraction is already in its simplest form.
The Result: Whether you use long division or a calculator, the answer to 4³ / 5³ (or 64 / 125) is 0.512.
Beyond the Calculation: Exploring the Broader Context
Solving 4³/5³ provides a stepping stone to understanding broader mathematical concepts. Let's delve into some of them:
1. The Power of Exponents: This problem highlights the significance of exponents in simplifying complex calculations. Instead of multiplying 4 by itself three times and then 5 by itself three times and then dividing the results, we can simplify the process by understanding the relationship between the cubed numbers.
2. Fraction Simplification: The process of attempting to simplify the fraction 64/125 reinforces the importance of understanding factors and greatest common divisors (GCD). Knowing when a fraction is in its simplest form is crucial for efficiency and accuracy.
3. Decimal Representation: The decimal equivalent, 0.512, provides a different perspective on the result. This representation is useful in various applications where decimal values are preferred.
4. Ratio and Proportion: We can view the result as a ratio—64 parts out of 125. This interpretation is valuable in contexts involving proportions and percentages.
Extending the Concept: Generalizing the Problem
Let's generalize the problem: (a³/b³). This can be simplified using the rule of exponents:
(a/b)³ = a³/b³
This means that dividing two numbers raised to the same power is equivalent to raising the quotient of the two numbers to that power. This principle has wide-ranging applications in various mathematical fields, including algebra and calculus.
Practical Applications: Where This Knowledge Matters
Understanding the principles behind this seemingly simple calculation isn't just an academic exercise. This knowledge has real-world applications in:
- Engineering: Calculations involving volume, especially when dealing with cubic measurements, frequently involve similar operations.
- Physics: Many physics problems, particularly those dealing with three-dimensional space and scaling, utilize cubic relationships.
- Computer Science: Algorithms and data structures often involve operations on exponents and powers.
- Finance: Compound interest calculations involve exponential growth, a concept directly related to exponents.
- Statistics: Data analysis sometimes utilizes functions involving cubic relationships.
Advanced Concepts and Further Exploration
For those seeking a deeper understanding, let's explore more advanced concepts related to this problem:
1. Rational Exponents: The concept extends to rational exponents (fractional powers) where the cube root plays a significant role. For example, understanding 4^(1/3) and 5^(1/3) would provide further insight.
2. Complex Numbers: The concepts can be extended to complex numbers, where the cube root takes on added complexity and multiple solutions.
3. Series and Sequences: Cubic relationships are prevalent in various series and sequences, such as geometric progressions.
Conclusion: Mastering the Fundamentals
The question "What is 4³ divided by 5³?" might initially seem trivial, but a deeper exploration reveals its significance in reinforcing core mathematical principles. From understanding exponents and fractions to appreciating the power of simplification and generalization, this seemingly simple calculation provides a robust foundation for more complex mathematical endeavors. Remember, mastering the fundamentals is key to unlocking higher-level concepts and applications. The more you understand the "why" behind mathematical operations, the more confident and proficient you'll become in tackling various problems. This comprehensive exploration not only provides the solution but also empowers you to approach similar problems with a broader understanding and enhanced problem-solving skills.
Latest Posts
Latest Posts
-
How Many Amps In 5000 Watts
May 11, 2025
-
26 Km Equals How Many Miles
May 11, 2025
-
How Much Is A 1 4 Pound Of Butter
May 11, 2025
-
Write The Slope Intercept Form Of The Equation For Each Line
May 11, 2025
-
What Uv Index Is Best To Tan
May 11, 2025
Related Post
Thank you for visiting our website which covers about What Is 4 3 Divided By 5 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.