What Is 4 Percent Of 100
Treneri
May 13, 2025 · 6 min read
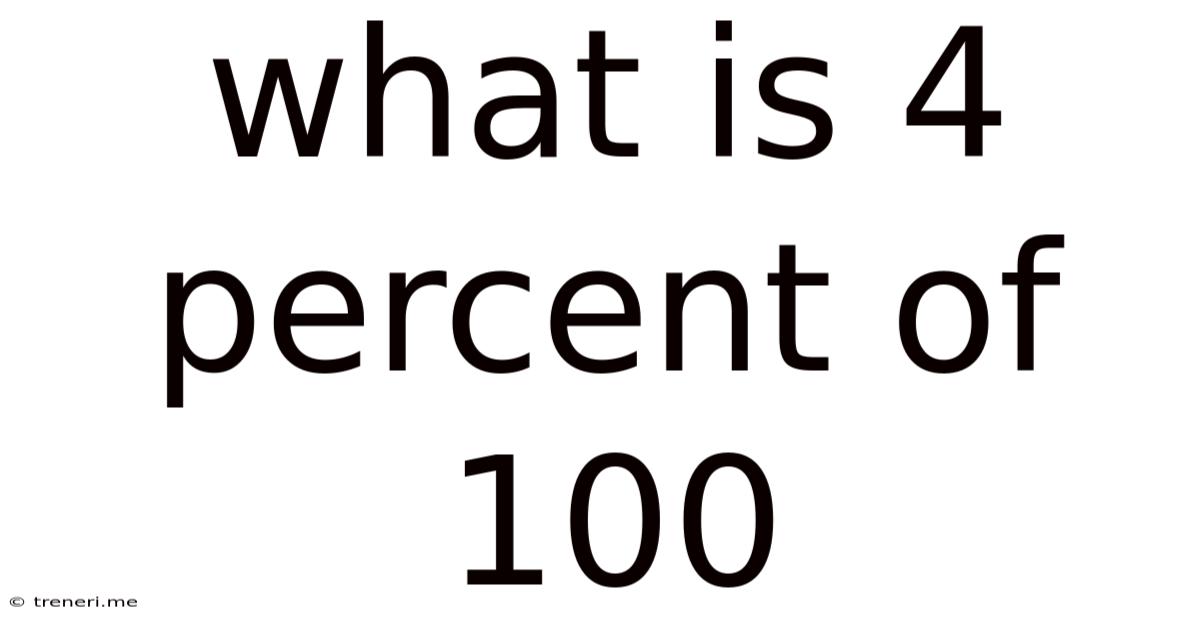
Table of Contents
What is 4 Percent of 100? A Deep Dive into Percentages and Their Applications
Calculating percentages is a fundamental skill with widespread applications in various aspects of life, from everyday budgeting to complex financial modeling. Understanding how to calculate percentages allows us to grasp proportions, make informed decisions, and interpret data effectively. This article delves into the seemingly simple question, "What is 4 percent of 100?", exploring the calculation process, its practical implications, and the broader context of percentage calculations.
Understanding Percentages: A Foundation
Before tackling the specific problem, let's establish a solid understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" denotes a percentage. For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5. This representation provides a standardized way to compare proportions and facilitate calculations.
Key Concepts:
- Percent: A ratio expressed as a fraction of 100.
- Fraction: A numerical representation of a part of a whole.
- Decimal: A number expressed in base-10 notation, using a decimal point to separate the whole and fractional parts.
Calculating 4 Percent of 100: Three Methods
There are several ways to calculate 4 percent of 100. Let's explore three common methods:
Method 1: Using the Fraction Method
This method involves converting the percentage to a fraction and then multiplying by the whole number.
- Convert the percentage to a fraction: 4% can be written as 4/100.
- Multiply the fraction by the whole number: (4/100) * 100 = 4
Therefore, 4 percent of 100 is 4.
Method 2: Using the Decimal Method
This method converts the percentage to a decimal and then multiplies it by the whole number.
- Convert the percentage to a decimal: 4% is equivalent to 0.04 (divide 4 by 100).
- Multiply the decimal by the whole number: 0.04 * 100 = 4
Again, we find that 4 percent of 100 is 4.
Method 3: Using the Proportion Method
This method sets up a proportion to solve for the unknown value.
- Set up a proportion: Let 'x' represent 4% of 100. We can write this as a proportion: x/100 = 4/100
- Solve for x: Cross-multiply to solve for x: 100x = 400. Divide both sides by 100: x = 4
This method confirms that 4 percent of 100 is indeed 4.
Practical Applications of Percentage Calculations
Understanding how to calculate percentages isn't just an academic exercise; it has numerous practical applications in daily life and professional settings. Let's explore some examples:
1. Financial Calculations:
- Interest Rates: Banks and financial institutions use percentages to calculate interest on loans and savings accounts. For example, understanding the interest rate on a loan helps you determine the total cost of borrowing.
- Discounts and Sales: Retailers frequently offer discounts expressed as percentages. Calculating the discounted price helps consumers make informed purchasing decisions.
- Taxes: Sales taxes, income taxes, and property taxes are all calculated using percentages. Knowing these rates allows for accurate budgeting and tax preparation.
- Tips and Gratuities: Restaurants and service providers often rely on tips calculated as a percentage of the total bill.
2. Data Analysis and Interpretation:
- Statistical Analysis: Percentages are fundamental in expressing proportions and trends in data sets. They provide a clear way to understand ratios and make comparisons.
- Surveys and Polls: Results from surveys and polls are often presented as percentages, enabling easy understanding of public opinion and preferences.
- Market Research: Businesses use percentages to analyze market share, customer demographics, and other key metrics to make strategic decisions.
3. Everyday Life:
- Recipe Scaling: Adjusting recipes based on the number of servings involves using percentages to increase or decrease ingredient quantities proportionally.
- Savings and Budgeting: Tracking savings and expenses as percentages of income aids in financial planning and identifying areas for improvement.
- Grade Calculation: In education, final grades are often calculated as weighted averages, with each assignment contributing a specific percentage to the overall grade.
Advanced Percentage Calculations: Beyond the Basics
While calculating 4 percent of 100 is straightforward, real-world applications often involve more complex percentage calculations. Let's explore some common scenarios:
1. Calculating Percentage Increase or Decrease:
Finding the percentage increase or decrease between two values involves determining the difference, dividing by the original value, and multiplying by 100.
For example: If a product's price increases from $100 to $120, the percentage increase is calculated as follows: (($120 - $100) / $100) * 100 = 20%.
2. Finding the Original Value:
Sometimes you know the percentage and the final value, and need to find the original value. This requires working backward using algebraic methods.
For example: If a discounted item costs $80 after a 20% discount, the original price can be calculated as: $80 / (1 - 0.20) = $100.
3. Calculating Compound Interest:
Compound interest involves earning interest not only on the principal but also on accumulated interest. The formula for compound interest is: A = P (1 + r/n)^(nt), where:
- A = the future value of the investment/loan, including interest
- P = the principal investment amount (the initial deposit or loan amount)
- r = the annual interest rate (decimal)
- n = the number of times that interest is compounded per year
- t = the number of years the money is invested or borrowed for
4. Percentage Points vs. Percentage Change:
It's crucial to differentiate between percentage points and percentage change. A percentage point refers to an absolute difference between two percentages, while percentage change refers to the relative change between two percentages.
For example: If interest rates increase from 2% to 5%, this is a 3 percentage point increase. However, the percentage change is calculated as ((5-2)/2)*100 = 150%.
Mastering Percentages: Tips and Resources
Mastering percentage calculations requires practice and a clear understanding of the underlying concepts. Here are some tips to enhance your skills:
- Practice Regularly: Solve various percentage problems to build confidence and fluency.
- Use Multiple Methods: Explore different calculation methods to find the approach that best suits your understanding.
- Utilize Online Calculators: While understanding the underlying principles is crucial, online calculators can be useful for checking your work or tackling complex problems.
- Seek Additional Resources: Explore educational websites, textbooks, and videos that offer detailed explanations and practice exercises.
Conclusion
The seemingly simple question, "What is 4 percent of 100?", opens the door to a world of practical applications for percentage calculations. From everyday budgeting to complex financial modeling, understanding percentages is a valuable skill that empowers informed decision-making and efficient problem-solving. By mastering the fundamental concepts and practicing various calculation methods, you can confidently navigate the world of percentages and leverage their power in diverse contexts. Remember to always double-check your calculations and seek further resources if needed. The ability to confidently work with percentages will significantly enhance your analytical skills and overall understanding of numerical data.
Latest Posts
Latest Posts
-
5 7 At 15 How Tall Will I Be
May 13, 2025
-
Conversao De Grau Fahrenheit Para Celsius
May 13, 2025
-
How Many Months Is 41 Years
May 13, 2025
-
2 382 Rounded To The Nearest Hundredth
May 13, 2025
-
How Many Lbs Is 6 8 Kg
May 13, 2025
Related Post
Thank you for visiting our website which covers about What Is 4 Percent Of 100 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.