What Is 4 Percent Of 20
Treneri
May 10, 2025 · 5 min read
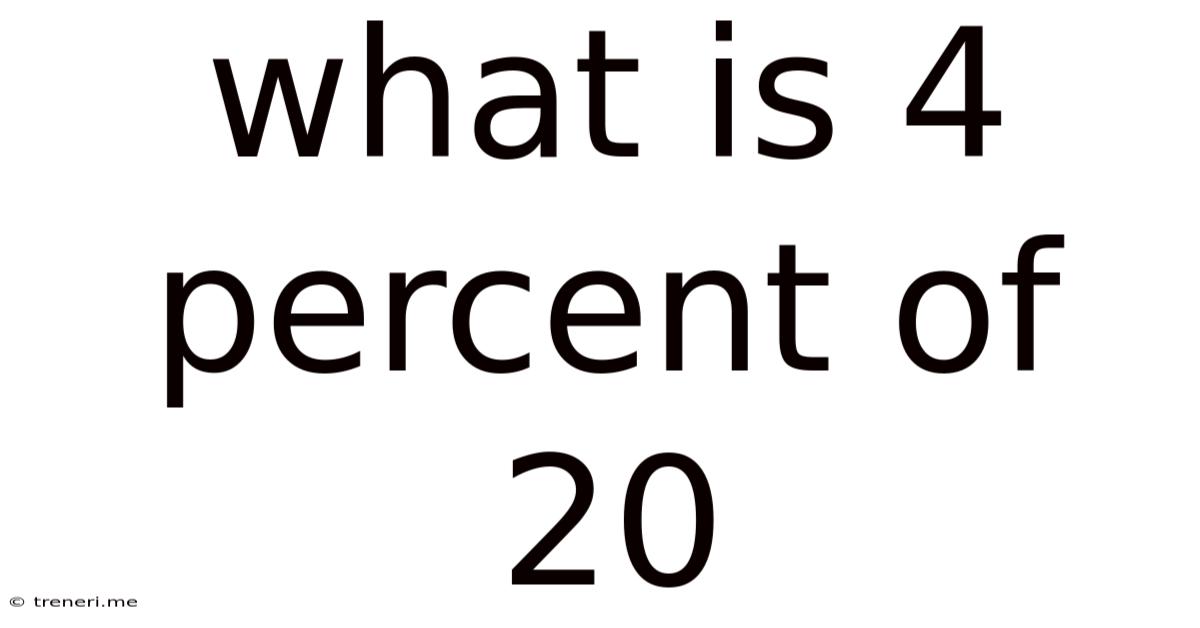
Table of Contents
What is 4 Percent of 20? A Deep Dive into Percentage Calculations
Calculating percentages is a fundamental skill with applications spanning numerous fields, from everyday budgeting and shopping to complex financial analysis and scientific research. Understanding how to calculate percentages not only improves your mathematical proficiency but also empowers you to make informed decisions in various aspects of life. This article delves into the seemingly simple question, "What is 4 percent of 20?" and, in doing so, explores the broader context of percentage calculations, offering practical examples and tips to master this crucial skill.
Understanding Percentages
Before we tackle the specific problem, let's clarify the concept of percentages. A percentage is simply a fraction expressed as a part of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of one hundred." Therefore, 4% means 4 out of 100, which can also be expressed as the fraction 4/100 or the decimal 0.04.
Calculating 4 Percent of 20: Three Methods
There are several ways to calculate 4 percent of 20. Let's explore three common methods:
Method 1: Using the Fraction Method
This method involves converting the percentage to a fraction and then multiplying it by the number.
- Step 1: Convert the percentage to a fraction: 4% = 4/100
- Step 2: Simplify the fraction (optional): 4/100 can be simplified to 1/25
- Step 3: Multiply the fraction by the number: (1/25) * 20 = 20/25
- Step 4: Simplify the resulting fraction: 20/25 simplifies to 4/5
- Step 5: Convert the fraction to a decimal: 4/5 = 0.8
Therefore, 4 percent of 20 is 0.8.
Method 2: Using the Decimal Method
This method involves converting the percentage to a decimal and then multiplying it by the number.
- Step 1: Convert the percentage to a decimal: 4% = 0.04 (divide 4 by 100)
- Step 2: Multiply the decimal by the number: 0.04 * 20 = 0.8
This method directly yields the answer in decimal form: 0.8.
Method 3: Using Proportions
This method sets up a proportion to solve for the unknown value.
- Step 1: Set up a proportion: x/20 = 4/100 (where 'x' represents 4% of 20)
- Step 2: Cross-multiply: 100x = 80
- Step 3: Solve for x: x = 80/100 = 0.8
This method also results in the answer 0.8.
Practical Applications: Real-World Examples
The ability to quickly and accurately calculate percentages is crucial in numerous everyday situations. Here are some examples:
-
Shopping Discounts: Imagine a shirt costs $20 and is on sale for 4% off. Using the methods described above, you'd quickly determine the discount is $0.80, resulting in a final price of $19.20.
-
Calculating Tips: If you want to leave a 4% tip on a $20 meal, you'd calculate 4% of $20, which is $0.80.
-
Understanding Interest Rates: Banks and financial institutions use percentages extensively. If you have a savings account with a 4% annual interest rate on a $20 balance, you'd earn $0.80 in interest over the year (simplified calculation).
-
Analyzing Data: In scientific research, business analytics, and various other fields, understanding percentages helps interpret data and draw meaningful conclusions. For example, if 4% of 20 survey respondents chose a particular option, this represents 0.8 respondents.
-
Commission Calculations: Salespeople often earn commission based on a percentage of their sales. If a salesperson earns 4% commission on a $20 sale, they earn $0.80.
Expanding Your Percentage Calculation Skills
Mastering percentage calculations involves more than just understanding the basic formulas. Here are some tips for improvement:
-
Practice Regularly: Consistent practice is key to solidifying your understanding and improving speed and accuracy. Try solving various percentage problems with different numbers.
-
Memorize Key Percentages: Familiarizing yourself with the decimal equivalents of common percentages (e.g., 10%, 25%, 50%, 75%) can significantly speed up calculations.
-
Use Calculators Strategically: While manual calculations are important for understanding the underlying concepts, using a calculator for complex or time-sensitive calculations is perfectly acceptable.
-
Check Your Work: Always double-check your answers to ensure accuracy. You can do this by using a different method or by estimating the answer.
-
Understand the Context: When dealing with real-world problems, always consider the context of the problem. This will help you interpret your results correctly.
Beyond the Basics: More Complex Percentage Problems
While calculating 4% of 20 is relatively straightforward, percentage problems can become more complex. You might encounter scenarios involving:
- Calculating Percentage Increase or Decrease: Determining the percentage change between two values.
- Finding the Original Value: Calculating a value before a percentage increase or decrease has been applied.
- Compound Interest: Calculating interest earned on both the principal and accumulated interest over multiple periods.
- Tax Calculations: Computing taxes based on percentages of income or purchase price.
These advanced percentage calculations often require a deeper understanding of mathematical principles and might involve the use of formulas or specialized calculators.
Conclusion: The Power of Percentage Knowledge
The seemingly simple question, "What is 4 percent of 20?" serves as a gateway to understanding the wider world of percentage calculations. This fundamental mathematical skill has widespread practical applications, impacting various aspects of our daily lives. By mastering the different methods for calculating percentages and practicing regularly, you will equip yourself with a valuable tool for making informed decisions, analyzing data effectively, and navigating the numerical world with confidence. Remember, consistent practice and a thorough understanding of the underlying principles are the keys to success in mastering percentages.
Latest Posts
Latest Posts
-
2 3 4 Plus 2 3 4
May 10, 2025
-
Center Of Mass Of Right Triangle
May 10, 2025
-
Sleep Calculator How Long Did I Sleep
May 10, 2025
-
What Is 8 40 As A Percentage
May 10, 2025
-
A Rectangle Is Removed From A Right Triangle
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Is 4 Percent Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.