What Is 4 Percent Of 5000
Treneri
Apr 05, 2025 · 5 min read
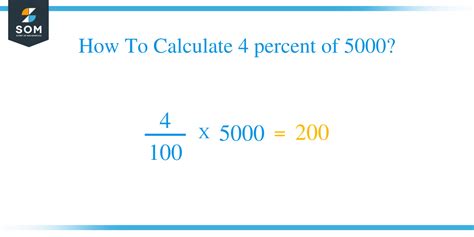
Table of Contents
What is 4 Percent of 5000? A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill with wide-ranging applications in various aspects of life, from finance and budgeting to understanding statistics and data analysis. This in-depth guide will not only answer the question, "What is 4 percent of 5000?" but also equip you with the knowledge and tools to confidently tackle similar percentage problems. We'll explore multiple methods for calculating percentages, delve into the underlying concepts, and showcase practical examples to solidify your understanding.
Understanding Percentages: The Basics
Before diving into the specific calculation, let's establish a solid foundation in understanding percentages. A percentage is simply a fraction or proportion expressed as a number out of 100. The symbol "%" signifies "per cent" or "out of one hundred". For example, 10% means 10 out of 100, which can be written as the fraction 10/100 or the decimal 0.10.
Understanding this fundamental concept is crucial for tackling percentage calculations. We'll break down several methods for calculating percentages, providing clarity and flexibility depending on your preference and the complexity of the problem.
Method 1: Using the Formula
The most straightforward method for calculating percentages involves using a simple formula:
Percentage = (Part/Whole) x 100%
In our case:
- Part: The value we want to find the percentage of (the unknown value – which is what we want to calculate).
- Whole: The total value (5000).
- Percentage: 4%
Let's apply the formula to find 4% of 5000:
Part = (Percentage/100%) x Whole
Part = (4%/100%) x 5000
Part = (0.04) x 5000
Part = 200
Therefore, 4% of 5000 is 200.
Method 2: Converting Percentage to a Decimal
Another efficient method involves converting the percentage directly into a decimal. To do this, simply divide the percentage by 100. In our case:
4% / 100 = 0.04
Then, multiply this decimal by the whole number:
0.04 x 5000 = 200
Again, we arrive at the answer: 4% of 5000 is 200.
Method 3: Using Proportions
Proportions offer a visual and intuitive way to solve percentage problems. We can set up a proportion to represent the relationship between the percentage and the total value:
4/100 = x/5000
To solve for 'x' (which represents 4% of 5000), we cross-multiply:
4 x 5000 = 100x
20000 = 100x
x = 20000/100
x = 200
This confirms our answer: 4% of 5000 is 200.
Practical Applications of Percentage Calculations
Understanding how to calculate percentages is essential in numerous real-world scenarios:
1. Finance and Budgeting:
- Calculating interest: Understanding interest rates is crucial for managing loans, investments, and savings accounts. Calculating the interest earned or paid involves using percentage calculations.
- Sales tax: Calculating sales tax on purchases requires determining a percentage of the purchase price.
- Discounts and markdowns: Calculating discounts offered during sales involves determining a percentage reduction in the original price.
- Investment returns: Tracking investment returns often involves calculating percentage increases or decreases in investment values.
- Profit margins: Businesses use percentage calculations to determine profit margins and assess the profitability of products or services.
2. Data Analysis and Statistics:
- Analyzing datasets: Percentages are frequently used to represent proportions within datasets, facilitating data interpretation and comparison.
- Presenting findings: Presenting data using percentages can make complex information more accessible and easier to understand.
- Statistical analysis: Many statistical analyses rely on percentage calculations for interpreting results and drawing conclusions.
3. Everyday Life:
- Calculating tips: Calculating a tip at a restaurant involves finding a percentage of the bill amount.
- Understanding surveys and polls: Interpreting results from surveys and polls often involves understanding percentages.
- Comparing prices: Percentages can be used to compare the prices of different products or services.
Advanced Percentage Calculations: Beyond the Basics
While the methods described above effectively handle simple percentage calculations, more complex scenarios may require a deeper understanding. Let's explore some of these:
1. Calculating Percentage Increase or Decrease:
Calculating percentage change involves determining the percentage difference between two values. The formula is:
Percentage Change = [(New Value - Old Value) / Old Value] x 100%
For example, if a product's price increases from $100 to $120, the percentage increase is:
[(120 - 100) / 100] x 100% = 20%
Conversely, if the price decreases from $120 to $100, the percentage decrease is:
[(100 - 120) / 120] x 100% = -16.67%
2. Finding the Original Value after a Percentage Change:
If you know the new value and the percentage change, you can calculate the original value using the following formula:
Original Value = New Value / (1 + Percentage Change/100%) (for percentage increase)
Original Value = New Value / (1 - Percentage Change/100%) (for percentage decrease)
For example, if a product is priced at $120 after a 20% increase, the original price was:
$120 / (1 + 20/100) = $100
3. Calculating Percentage Points:
It's crucial to distinguish between percentage change and percentage points. Percentage points represent the arithmetic difference between two percentages, not the percentage change. For instance, if a company's market share increases from 20% to 25%, the increase is 5 percentage points, not a 25% increase.
Conclusion: Mastering Percentage Calculations
The ability to calculate percentages is a valuable skill applicable across many fields. By understanding the fundamental concepts and mastering the various methods presented in this guide, you can confidently tackle various percentage problems, from simple calculations to more complex scenarios. Remember to choose the method most comfortable and efficient for you, and practice regularly to build your proficiency. Whether you're managing finances, analyzing data, or navigating everyday tasks, your mastery of percentage calculations will significantly enhance your understanding and problem-solving abilities. This comprehensive guide provides you with the tools to approach percentage calculations with confidence and accuracy. With consistent practice and application, you'll quickly find yourself proficient in this essential skill.
Latest Posts
Latest Posts
-
How To Calculate A Board Foot Of Lumber
Apr 05, 2025
-
16 X 16 Is How Many Square Feet
Apr 05, 2025
-
227 Out Of 245 Is Waht Grade
Apr 05, 2025
-
3 4 Cup Dry Pasta Is How Much Cooked
Apr 05, 2025
-
2 To The Power Of 31
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about What Is 4 Percent Of 5000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
