What Is 4 To The 5 Power
Treneri
May 14, 2025 · 5 min read
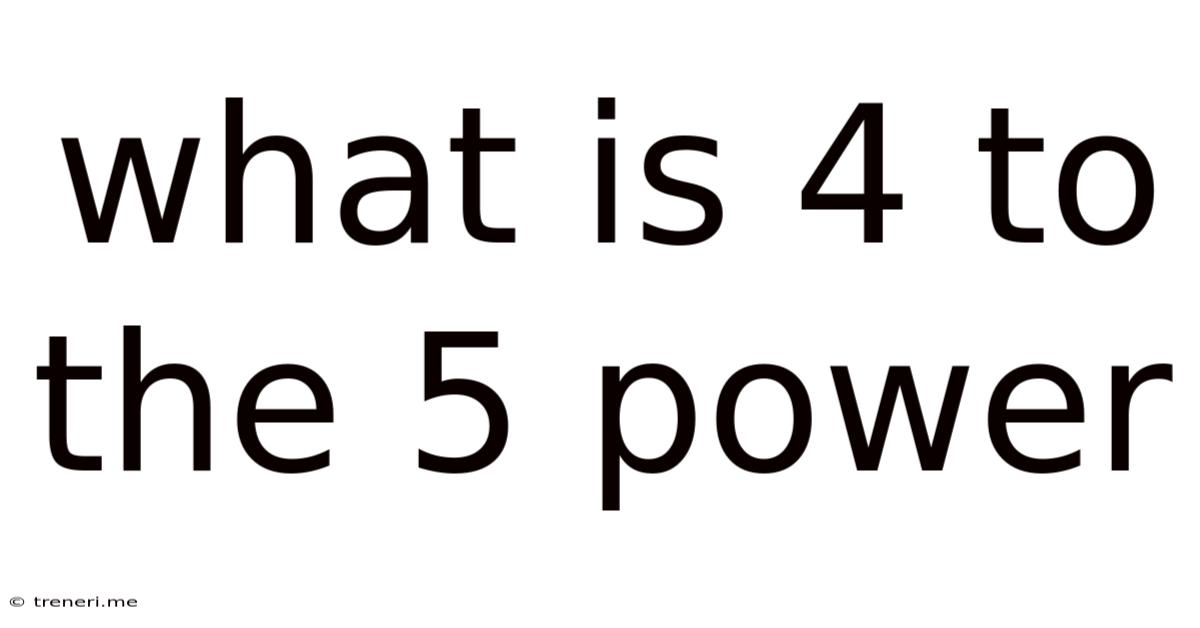
Table of Contents
What is 4 to the 5th Power? A Deep Dive into Exponents and Their Applications
Understanding exponents is fundamental to mathematics and numerous fields, from simple calculations to complex scientific modeling. This article delves deep into the concept of "4 to the 5th power," explaining what it means, how to calculate it, and exploring its broader implications within mathematics and beyond. We'll uncover the underlying principles, explore practical applications, and tackle related concepts to provide a comprehensive understanding.
Deciphering the Notation: 4⁵
The expression "4 to the 5th power," written mathematically as 4⁵, represents repeated multiplication. The base number, 4, is multiplied by itself the number of times indicated by the exponent, 5. Therefore, 4⁵ means:
4 * 4 * 4 * 4 * 4
This seemingly simple notation unlocks a powerful concept with far-reaching consequences in various disciplines.
Calculating 4 to the 5th Power
Calculating 4⁵ is straightforward:
- Step 1: Start with the base number, 4.
- Step 2: Multiply 4 by itself: 4 * 4 = 16
- Step 3: Multiply the result by 4 again: 16 * 4 = 64
- Step 4: Continue multiplying by 4: 64 * 4 = 256
- Step 5: Finally, multiply by 4 one last time: 256 * 4 = 1024
Therefore, 4 to the 5th power is 1024.
Beyond the Calculation: Understanding Exponents
The concept of exponents extends far beyond this single calculation. Understanding exponents allows us to express incredibly large or small numbers concisely and to perform complex calculations efficiently. Here's a breakdown of key aspects:
The Base and the Exponent
- Base: The base is the number being multiplied repeatedly (in our case, 4).
- Exponent: The exponent (also called the power or index) indicates how many times the base is multiplied by itself (in our case, 5).
Properties of Exponents
Exponents follow specific rules that simplify calculations and problem-solving:
- Product of Powers: When multiplying two numbers with the same base, add the exponents: aᵐ * aⁿ = a⁽ᵐ⁺ⁿ⁾
- Quotient of Powers: When dividing two numbers with the same base, subtract the exponents: aᵐ / aⁿ = a⁽ᵐ⁻ⁿ⁾
- Power of a Power: When raising a power to another power, multiply the exponents: (aᵐ)ⁿ = a⁽ᵐⁿ⁾
- Power of a Product: When raising a product to a power, raise each factor to that power: (ab)ⁿ = aⁿbⁿ
- Power of a Quotient: When raising a quotient to a power, raise both the numerator and the denominator to that power: (a/b)ⁿ = aⁿ/bⁿ
These properties are crucial for manipulating and simplifying expressions involving exponents.
Negative Exponents
Negative exponents represent reciprocals. For example, 4⁻⁵ is the reciprocal of 4⁵:
4⁻⁵ = 1 / 4⁵ = 1 / 1024
Fractional Exponents
Fractional exponents represent roots. For example, 4^(1/2) is the square root of 4, and 4^(1/3) is the cube root of 4.
Zero Exponent
Any non-zero number raised to the power of zero is equal to 1: a⁰ = 1 (where a ≠ 0).
Applications of Exponents
Exponents have wide-ranging applications across numerous fields:
Science and Engineering
-
Compound Interest: The growth of investments over time is calculated using exponential functions. The formula A = P(1 + r/n)^(nt) showcases exponential growth where 'A' is the future value, 'P' is the principal amount, 'r' is the annual interest rate, 'n' is the number of times that interest is compounded per year, and 't' is the number of years.
-
Radioactive Decay: The decay of radioactive materials follows an exponential decay model, which can be expressed with the formula N(t) = N₀e^(-λt), where 'N(t)' is the amount of material remaining at time 't', 'N₀' is the initial amount, 'λ' is the decay constant, and 'e' is the base of the natural logarithm.
-
Population Growth: Exponential functions are used to model population growth in various biological and ecological contexts.
-
Signal Processing: Exponents are extensively used in signal processing for operations such as amplitude modulation and frequency analysis.
Computer Science
-
Binary Numbers: Computers use binary numbers (base-2) which heavily rely on exponents for representing numbers.
-
Big O Notation: In computer science, Big O notation uses exponents to describe the efficiency of algorithms. For instance, an algorithm with O(n²) complexity has a runtime proportional to the square of the input size.
-
Data Structures and Algorithms: Many data structures and algorithms leverage the principles of exponents for their design and implementation, contributing to their efficiency and scalability.
Finance
-
Compounding Interest: As already mentioned, understanding exponential growth is crucial for calculating compound interest, a cornerstone of financial planning and investment strategies.
-
Financial Modeling: Many financial models use exponential functions to simulate and predict market behavior, risk assessment, and portfolio optimization.
Other Applications
-
Physics: Exponents are prevalent in physics, describing phenomena like gravitational forces, exponential decay of charge in a capacitor, and radioactive decay.
-
Chemistry: Exponential functions are involved in chemical reaction rates and kinetics.
-
Biology: Population growth and decay in biological systems often follow exponential patterns.
-
Economics: Exponential functions are used in economic models to represent growth, decay, and other dynamic processes.
Expanding Your Knowledge: Related Concepts
To further solidify your understanding of exponents, consider exploring these related mathematical concepts:
-
Logarithms: Logarithms are the inverse function of exponents. They provide a way to solve for the exponent when the base and result are known.
-
Scientific Notation: Scientific notation uses exponents to represent very large or very small numbers concisely.
-
Exponential Functions: Exponential functions are functions where the independent variable appears as an exponent. These functions have characteristic exponential growth or decay patterns.
Conclusion: The Power of Exponents
The seemingly simple calculation of 4 to the 5th power reveals the power and versatility of exponents. This fundamental concept underpins a wide array of mathematical, scientific, and technological applications. Understanding exponents not only enables you to perform specific calculations but also empowers you to comprehend and model complex phenomena across numerous disciplines. From understanding compound interest to comprehending the decay of radioactive materials and the growth of populations, the principles of exponents are far-reaching and continue to play an increasingly important role in our technological and scientific advancements. By exploring the underlying principles, properties, and diverse applications discussed here, you are well-equipped to effectively utilize and further appreciate the world of exponents.
Latest Posts
Latest Posts
-
12 Minute Run Vo2 Max Calculator
May 14, 2025
-
What Does 36 24 36 Mean
May 14, 2025
-
How Many Cups Is 1 3 Of A Gallon
May 14, 2025
-
Cuantos Segundos Hay En Un Minuto
May 14, 2025
-
How To Calculate Density From Relative Density
May 14, 2025
Related Post
Thank you for visiting our website which covers about What Is 4 To The 5 Power . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.