What Is 50 Percent Of 100
Treneri
May 11, 2025 · 5 min read
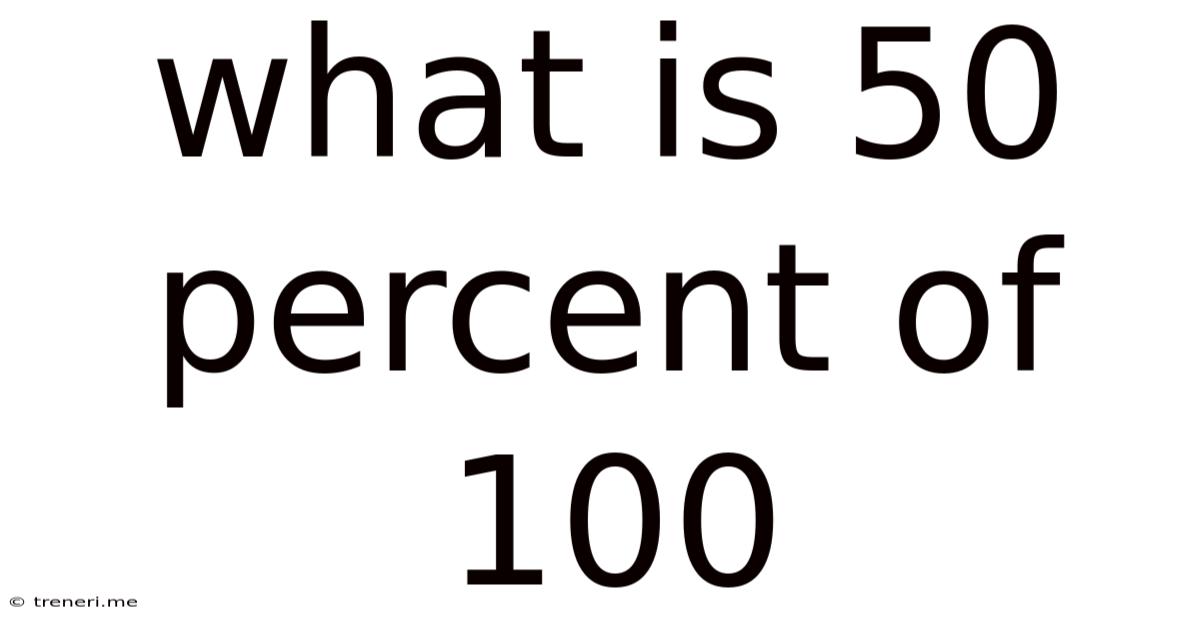
Table of Contents
What is 50 Percent of 100? A Deep Dive into Percentages and Their Applications
The seemingly simple question, "What is 50 percent of 100?" opens the door to a vast world of mathematical concepts, practical applications, and real-world scenarios where understanding percentages is crucial. While the answer itself is straightforward – 50 – the journey to understanding how to arrive at this answer and the broader implications of percentage calculations is far more enriching. This article will not only answer the question directly but delve into the intricacies of percentages, exploring their various uses and providing you with the tools to tackle similar calculations confidently.
Understanding Percentages: The Foundation
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" is derived from the Latin words "per centum," meaning "out of a hundred." This foundational understanding is key to grasping percentage calculations. Essentially, a percentage represents a portion of a whole, where the whole is always considered to be 100%.
The Percentage Formula: A Simple Equation
The basic formula for calculating percentages is:
(Percentage/100) x Whole = Part
Or, conversely:
(Part/Whole) x 100 = Percentage
These formulas are interchangeable and allow you to solve for any of the three variables – percentage, whole, or part – given the other two.
Calculating 50% of 100: A Step-by-Step Approach
Now, let's apply this knowledge to our original question: What is 50 percent of 100?
Using the first formula:
(50/100) x 100 = 50
This calculation clearly demonstrates that 50% of 100 is 50. The fraction 50/100 simplifies to 1/2, meaning we are essentially finding half of 100.
Beyond the Basics: Expanding Our Understanding
While the calculation itself is simple, understanding percentages extends far beyond this basic example. Let's explore some broader applications and related concepts:
1. Percentage Increase and Decrease: Tracking Changes
Percentages are invaluable tools for tracking changes over time. Whether it's the growth of a company's profits, the fluctuation of stock prices, or the increase in a population, percentages provide a standardized way to represent these changes.
The formula for calculating percentage increase is:
[(New Value - Old Value) / Old Value] x 100 = Percentage Increase
Conversely, for percentage decrease:
[(Old Value - New Value) / Old Value] x 100 = Percentage Decrease
Example: If a company's profit increased from $100 to $150, the percentage increase would be:
[(150 - 100) / 100] x 100 = 50%
2. Percentage Points vs. Percentage Change: A Crucial Distinction
It's crucial to differentiate between "percentage points" and "percentage change." A percentage point refers to an absolute difference between two percentages, while a percentage change represents the relative difference.
Example: If interest rates rise from 5% to 10%, the increase is 5 percentage points. However, the percentage change is a 100% increase [(10-5)/5 x 100 = 100%]. This distinction is important for clear communication and accurate analysis.
3. Applications in Various Fields: Real-World Examples
Percentages find application in a multitude of fields:
- Finance: Calculating interest rates, loan repayments, investment returns, and tax rates.
- Retail: Determining discounts, markups, and profit margins.
- Science: Expressing experimental results, statistical data, and probabilities.
- Statistics: Analyzing data sets, representing distributions, and making inferences.
- Everyday Life: Understanding tips, sales taxes, and various proportions.
4. Working with Fractions and Decimals: Interchangeability
Percentages are easily converted to fractions and decimals, and vice versa. This interchangeability is crucial for performing complex calculations.
- Percentage to Decimal: Divide the percentage by 100. (50% = 0.50)
- Percentage to Fraction: Express the percentage as a fraction with a denominator of 100, then simplify. (50% = 50/100 = 1/2)
- Decimal to Percentage: Multiply the decimal by 100. (0.50 x 100 = 50%)
- Fraction to Percentage: Convert the fraction to a decimal, then multiply by 100. (1/2 = 0.50 x 100 = 50%)
5. Solving for the Whole or the Percentage: Inverse Calculations
The percentage formula can be rearranged to solve for the whole or the percentage, given the other two values.
- Finding the Whole: If you know the part and the percentage, rearrange the formula: Whole = (Part x 100) / Percentage
- Finding the Percentage: If you know the part and the whole, use the formula: Percentage = (Part / Whole) x 100
Advanced Percentage Calculations: Tackling Complex Scenarios
While the basic percentage calculation is straightforward, many real-world problems involve multiple steps or more complex scenarios. Let's explore some examples:
- Compound Interest: This involves calculating interest on both the principal amount and accumulated interest. The formula is more complex, but the fundamental concept of percentage remains central.
- Percentage Change over Multiple Periods: Calculating the overall percentage change after several increases or decreases requires careful consideration of the order of operations and the cumulative effect of the changes.
- Weighted Averages: This involves assigning different weights to different values before calculating the average percentage.
Conclusion: Mastering Percentages for Success
Understanding percentages is a fundamental skill with widespread applications in various aspects of life. From basic calculations to complex financial analyses, the ability to work confidently with percentages is crucial. This article provides a comprehensive overview of the subject, moving from the basic calculation of 50% of 100 to exploring advanced concepts and real-world applications. By mastering these concepts, you’ll equip yourself with a powerful tool for navigating numerical challenges and making informed decisions in various contexts. Remember the fundamental formulas and the importance of distinguishing between percentage points and percentage change, and you'll be well on your way to mastering the world of percentages.
Latest Posts
Latest Posts
-
What Wire Size For 30 Amps 220 Volts
May 12, 2025
-
Square Root Of 4 Multiplied 16
May 12, 2025
-
60 Days From September 14 2024
May 12, 2025
-
How Many Days Is 267 Hours
May 12, 2025
-
1 Out Of 30 As A Percentage
May 12, 2025
Related Post
Thank you for visiting our website which covers about What Is 50 Percent Of 100 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.