What Is 50 Percent Of 16
Treneri
May 14, 2025 · 5 min read
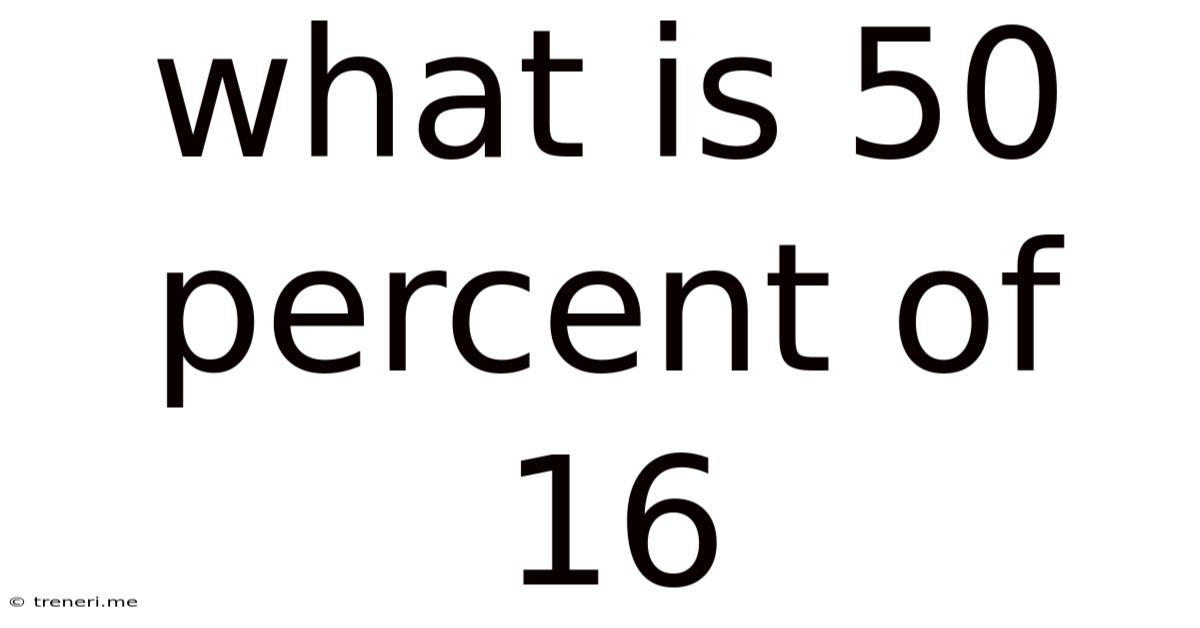
Table of Contents
What is 50 Percent of 16? A Deep Dive into Percentages and Their Applications
This seemingly simple question, "What is 50 percent of 16?", opens the door to a fascinating exploration of percentages, their fundamental principles, and their widespread applications in various fields. While the answer itself is straightforward, understanding the underlying concepts allows us to confidently tackle more complex percentage problems and appreciate their significance in our daily lives.
Understanding Percentages: The Basics
A percentage is simply a fraction expressed as a part of 100. The word "percent" literally means "per hundred" or "out of 100." We represent percentages using the "%" symbol. For example, 50% can be understood as 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5 as a decimal.
Key Concepts:
- Fraction to Percentage: To convert a fraction to a percentage, divide the numerator by the denominator and multiply by 100. For example, 1/4 = (1 ÷ 4) x 100 = 25%.
- Decimal to Percentage: To convert a decimal to a percentage, multiply by 100 and add the "%" symbol. For example, 0.75 = 0.75 x 100 = 75%.
- Percentage to Decimal: To convert a percentage to a decimal, divide by 100. For example, 60% = 60 ÷ 100 = 0.6.
- Percentage to Fraction: To convert a percentage to a fraction, write the percentage as a fraction with a denominator of 100 and then simplify. For example, 20% = 20/100 = 1/5.
Calculating 50% of 16: The Simple Method
Calculating 50% of 16 is particularly easy because 50% is equivalent to 1/2. Therefore, finding 50% of 16 is the same as finding half of 16. Simply divide 16 by 2:
16 ÷ 2 = 8
Therefore, 50% of 16 is 8.
Calculating 50% of 16: The General Method
While the above method is efficient for 50%, let's explore the general method applicable to any percentage calculation. This method involves three steps:
-
Convert the percentage to a decimal: 50% becomes 0.50 (or simply 0.5).
-
Multiply the decimal by the number: 0.5 x 16 = 8
-
The result is the answer: Therefore, 50% of 16 is 8.
This general method is crucial for calculating percentages that aren't as easily simplified as 50%.
Real-World Applications of Percentage Calculations
Percentage calculations are ubiquitous in our daily lives. Here are some examples:
-
Sales and Discounts: Stores frequently offer discounts expressed as percentages. For example, a 20% discount on a $100 item means you save 20% of $100, which is $20. The final price would be $80.
-
Taxes and Tips: Sales tax is often calculated as a percentage of the purchase price. Similarly, tipping in restaurants is usually expressed as a percentage of the bill.
-
Interest Rates: Interest rates on loans, savings accounts, and investments are expressed as percentages. Understanding these percentages is crucial for making informed financial decisions.
-
Statistics and Data Analysis: Percentages are fundamental in presenting and interpreting data. For example, survey results, election polls, and economic indicators are often presented using percentages.
-
Grade Calculations: Academic grades are frequently calculated as percentages of total points earned.
-
Growth and Decay: In science and finance, percentage changes are used to represent growth (e.g., population growth, investment returns) or decay (e.g., radioactive decay, asset depreciation).
-
Proportions and Ratios: Percentages provide a standardized way to compare quantities.
Advanced Percentage Problems: Building on the Foundation
Now that we understand the basics, let's consider more complex scenarios:
Example 1: Finding the Original Price After a Discount:
A shirt is on sale for $60 after a 25% discount. What was the original price?
-
Let 'x' represent the original price.
-
The discount amount is 25% of x, or 0.25x.
-
The sale price is the original price minus the discount: x - 0.25x = 0.75x
-
We know the sale price is $60, so 0.75x = 60.
-
Solve for x: x = 60 / 0.75 = $80
Therefore, the original price was $80.
Example 2: Calculating Percentage Increase or Decrease:
A stock price increased from $50 to $60. What is the percentage increase?
-
Calculate the difference: $60 - $50 = $10
-
Divide the difference by the original price: $10 / $50 = 0.2
-
Multiply by 100 to express as a percentage: 0.2 x 100 = 20%
Therefore, the stock price increased by 20%.
The Importance of Accurate Percentage Calculations
Accuracy in percentage calculations is crucial in many contexts. Inaccurate calculations can lead to significant financial errors, misinterpretations of data, and flawed decision-making. Therefore, it's essential to develop a solid understanding of percentage principles and to double-check calculations whenever possible. Using calculators and spreadsheets can help ensure accuracy, particularly when dealing with more complex problems.
Beyond the Basics: Exploring Further
The world of percentages extends far beyond simple calculations like finding 50% of 16. Further exploration might involve learning about:
-
Compound interest: Interest earned not only on the principal but also on accumulated interest.
-
Exponential growth and decay: Models used to describe phenomena where the rate of change is proportional to the current value.
-
Statistical significance testing: Using percentages to determine the likelihood of observed results being due to chance.
-
Financial modeling: Utilizing percentages in complex financial analyses and projections.
In conclusion, while the answer to "What is 50 percent of 16?" is simply 8, the underlying concepts and applications of percentages are far-reaching and deeply relevant to numerous aspects of life. Mastering percentage calculations empowers us to navigate everyday situations, make informed decisions, and analyze data effectively. The simple question serves as a gateway to a deeper understanding of a fundamental mathematical concept with widespread practical implications.
Latest Posts
Latest Posts
-
What Is The Gcf Of 3 And 15
May 15, 2025
-
What Is 235 Rounded To The Nearest Ten
May 15, 2025
-
399 Rounded To The Nearest Hundred
May 15, 2025
-
Finding Heat Capacity Of A Calorimeter
May 15, 2025
-
56980 Rounded To The Nearest Hundred
May 15, 2025
Related Post
Thank you for visiting our website which covers about What Is 50 Percent Of 16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.