What Is 6/9 In Simplest Form
Treneri
May 12, 2025 · 5 min read
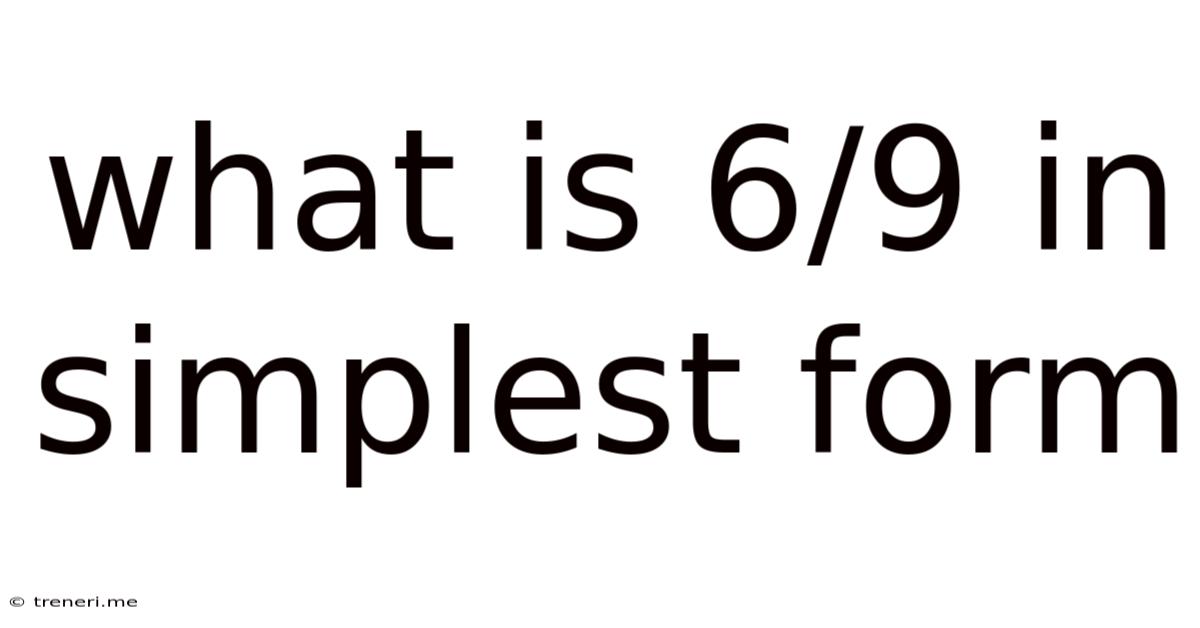
Table of Contents
What is 6/9 in Simplest Form? A Comprehensive Guide to Fraction Simplification
Understanding fractions is a fundamental concept in mathematics, crucial for various applications in everyday life and advanced studies. Simplifying fractions, also known as reducing fractions to their lowest terms, is a key skill that builds upon this foundation. This comprehensive guide delves into the process of simplifying fractions, using the example of 6/9 to illustrate the techniques involved. We’ll explore the concept, methods, and applications, providing a clear and insightful understanding of this important mathematical operation.
Understanding Fractions: Numerator, Denominator, and the Whole
Before we dive into simplifying 6/9, let's refresh our understanding of fractions. A fraction represents a part of a whole. It is written as a ratio of two numbers:
- Numerator: The top number represents the number of parts we have.
- Denominator: The bottom number represents the total number of equal parts the whole is divided into.
For example, in the fraction 6/9, 6 is the numerator and 9 is the denominator. This means we have 6 parts out of a total of 9 equal parts.
Simplifying Fractions: Finding the Greatest Common Divisor (GCD)
Simplifying a fraction means finding an equivalent fraction where the numerator and denominator are smaller, but the fraction's value remains the same. This is achieved by finding the Greatest Common Divisor (GCD), also known as the Greatest Common Factor (GCF), of the numerator and the denominator. The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
Several methods exist for finding the GCD:
1. Listing Factors:
This method involves listing all the factors of both the numerator and the denominator and identifying the largest common factor.
- Factors of 6: 1, 2, 3, 6
- Factors of 9: 1, 3, 9
The largest common factor is 3.
2. Prime Factorization:
This method involves expressing both the numerator and the denominator as a product of their prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself (e.g., 2, 3, 5, 7, 11...).
- Prime factorization of 6: 2 x 3
- Prime factorization of 9: 3 x 3
The common prime factor is 3. Therefore, the GCD is 3.
3. Euclidean Algorithm:
This is a more efficient method for larger numbers. It involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCD.
- Divide 9 by 6: 9 = 6 x 1 + 3
- Divide 6 by the remainder 3: 6 = 3 x 2 + 0
The last non-zero remainder is 3, so the GCD is 3.
Simplifying 6/9: Applying the GCD
Now that we've determined the GCD of 6 and 9 is 3, we can simplify the fraction:
Divide both the numerator and the denominator by the GCD (3):
6 ÷ 3 / 9 ÷ 3 = 2/3
Therefore, the simplest form of 6/9 is 2/3. This means that 6/9 and 2/3 represent the same value; they are equivalent fractions.
Visual Representation: Understanding the Equivalence
Imagine a pizza cut into 9 equal slices. 6/9 means you have 6 out of 9 slices. If you group the slices into sets of 3, you'll have 2 groups out of 3 total groups. This visually demonstrates that 6/9 is equivalent to 2/3.
Applications of Fraction Simplification
Simplifying fractions is a vital skill with numerous applications:
- Everyday Calculations: When dealing with recipes, measurements, or sharing items, simplifying fractions makes calculations easier and more understandable.
- Algebra and Calculus: Simplifying fractions is crucial for manipulating algebraic expressions and solving equations in higher-level mathematics.
- Data Analysis and Statistics: Simplifying fractions helps in interpreting and presenting data in a clear and concise manner.
- Geometry and Measurement: Simplifying fractions is used in calculations involving areas, volumes, and other geometric properties.
Common Mistakes to Avoid When Simplifying Fractions
- Dividing only the numerator or denominator: Remember to divide both the numerator and the denominator by the GCD.
- Not finding the greatest common divisor: Ensure you find the largest number that divides both the numerator and the denominator without leaving a remainder. Using a smaller common factor will result in a simplified fraction, but not the simplest form.
- Incorrect prime factorization: Ensure you correctly identify the prime factors of the numerator and the denominator to accurately determine the GCD.
Beyond 6/9: Practicing Fraction Simplification
Mastering fraction simplification requires practice. Try simplifying these fractions:
- 12/18
- 15/25
- 24/36
- 42/56
- 100/150
By consistently practicing these exercises, you will become more proficient in identifying the GCD and simplifying fractions quickly and accurately.
Conclusion: The Importance of Fraction Simplification
Simplifying fractions is more than just a mathematical procedure; it's a fundamental skill that enhances mathematical understanding and problem-solving abilities. The example of 6/9 not only illustrates the process but also highlights the importance of finding the greatest common divisor and the equivalence of fractions. By mastering this skill, you'll be better equipped to tackle more complex mathematical concepts and apply your knowledge in various real-world scenarios. Remember to practice regularly to solidify your understanding and build confidence in working with fractions. Through consistent practice and a clear understanding of the underlying principles, you can confidently navigate the world of fractions and utilize them effectively in various contexts.
Latest Posts
Latest Posts
-
Cuantas Son 16 Onzas En Litros
May 12, 2025
-
Calculating Heat Loss In A House
May 12, 2025
-
How Many Zeptoseconds Are In A Year
May 12, 2025
-
How Old Is Someone Born November 2005
May 12, 2025
-
How Many Miles In 1000 Km
May 12, 2025
Related Post
Thank you for visiting our website which covers about What Is 6/9 In Simplest Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.