What Is 6 Percent Of 40
Treneri
May 12, 2025 · 5 min read
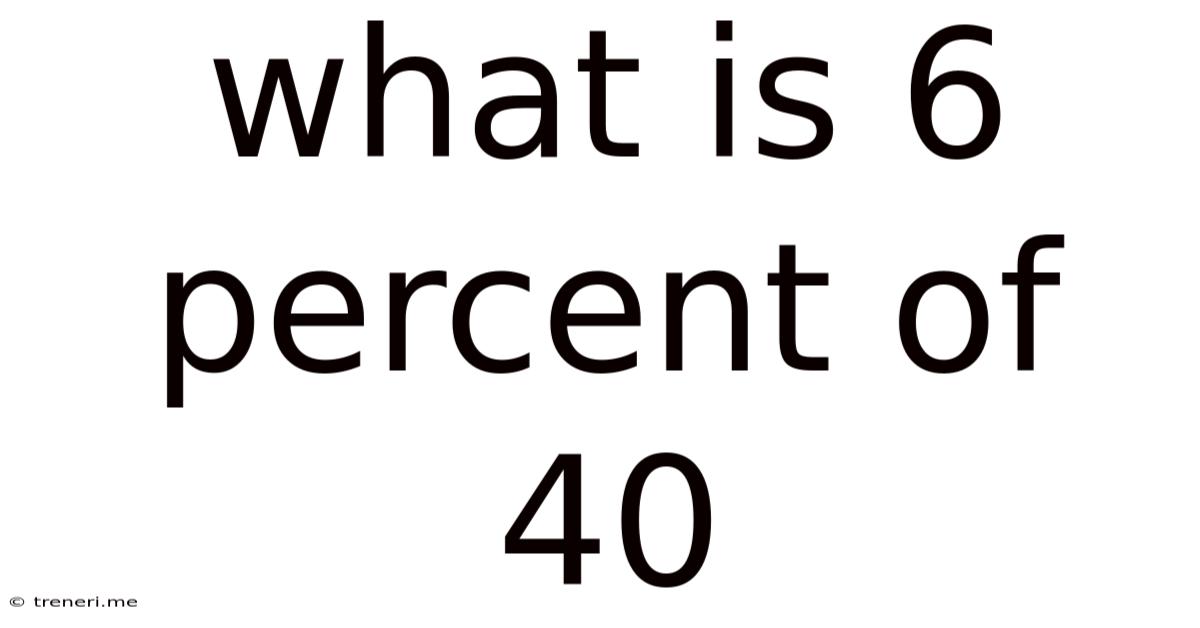
Table of Contents
What is 6 Percent of 40? A Deep Dive into Percentages and Their Applications
Calculating percentages is a fundamental skill with widespread applications in various aspects of life, from finance and budgeting to sales, discounts, and understanding statistics. This article will not only answer the question, "What is 6 percent of 40?" but will also delve into the underlying principles of percentage calculations, explore different methods for solving such problems, and showcase real-world examples where this type of calculation is essential.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "per hundred" or "out of 100." For instance, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
Understanding percentages involves grasping the relationship between three key components:
- The Percentage: This is the rate or proportion expressed as a number followed by the "%" symbol (e.g., 6%).
- The Whole: This is the total amount or the base value you are considering (e.g., 40 in our case).
- The Part: This is the portion of the whole that represents the percentage (e.g., the result of 6% of 40).
The fundamental formula for calculating percentages is:
(Percentage/100) * Whole = Part
Calculating 6 Percent of 40
Now, let's address the core question: What is 6 percent of 40? Using the formula above:
(6/100) * 40 = 2.4
Therefore, 6 percent of 40 is 2.4.
Alternative Methods for Calculating Percentages
While the above formula is the most straightforward approach, there are other ways to calculate percentages, each offering its own advantages depending on the context and your comfort level with mathematical operations:
Method 1: Using Decimal Equivalents
Convert the percentage to its decimal equivalent by dividing it by 100. 6% becomes 0.06. Then, multiply the decimal by the whole number:
0.06 * 40 = 2.4
This method is efficient and particularly useful when using calculators.
Method 2: Using Fractions
Convert the percentage to a fraction. 6% can be written as 6/100. Simplify the fraction if possible (in this case, it simplifies to 3/50). Then, multiply the fraction by the whole number:
(3/50) * 40 = (3 * 40) / 50 = 120 / 50 = 2.4
This method is helpful in understanding the proportional relationship between the percentage, the whole, and the part.
Method 3: Using Proportions
Set up a proportion:
6/100 = x/40
Cross-multiply and solve for x:
100x = 6 * 40 100x = 240 x = 240 / 100 x = 2.4
This method highlights the proportional relationship and is useful for understanding the underlying logic behind percentage calculations.
Real-World Applications of Percentage Calculations
Percentage calculations are ubiquitous in everyday life. Here are some examples:
1. Sales and Discounts:
Imagine a store offering a 6% discount on an item priced at $40. The discount amount would be 6% of $40, which is $2.40. The final price after the discount would be $40 - $2.40 = $37.60.
2. Taxes:
Sales taxes are often expressed as a percentage. If the sales tax rate is 6%, and you buy an item for $40, the tax amount would be 6% of $40, or $2.40. Your total cost would be $40 + $2.40 = $42.40.
3. Interest Rates:
Interest rates on loans and investments are usually expressed as percentages. If you invest $40 and earn a 6% annual interest, you would earn $2.40 in interest after one year.
4. Tips and Gratuities:
Calculating tips in restaurants often involves percentages. A 6% tip on a $40 meal would be $2.40.
5. Financial Statements:
Percentage calculations are crucial for analyzing financial statements. Profit margins, growth rates, and debt ratios are all expressed as percentages.
6. Statistical Analysis:
Percentages are widely used in presenting and interpreting statistical data. For example, survey results are often expressed as percentages to show the proportion of respondents who chose a particular option.
Beyond the Basics: More Complex Percentage Problems
While calculating 6% of 40 is a relatively simple calculation, the principles involved extend to more complex scenarios:
-
Finding the Percentage: If you know the part and the whole, you can find the percentage by dividing the part by the whole and multiplying by 100. For instance, if 2.4 is 6% of a number, what is the number? The solution involves solving the equation: (x/100) * 40 = 2.4, which leads to x = 6.
-
Finding the Whole: If you know the part and the percentage, you can find the whole by dividing the part by the percentage (expressed as a decimal) and multiplying by 100. For instance, if 2.4 represents 6% of a certain amount, what is that amount? The solution is 2.4 / 0.06 * 100 = 40.
-
Compound Interest: Calculating compound interest involves applying percentages repeatedly over time. This type of calculation is crucial in understanding investment growth and loan repayments.
-
Percentage Increase and Decrease: These calculations involve finding the percentage change between two values. The formula for percentage increase is [(New Value - Old Value) / Old Value] * 100. The formula for percentage decrease is [(Old Value - New Value) / Old Value] * 100.
Conclusion: Mastering Percentages for Everyday Success
Understanding percentages is a valuable life skill with far-reaching applications in numerous aspects of our daily lives. Mastering these calculations empowers you to make informed financial decisions, understand statistical data, and confidently navigate various situations where proportional relationships are involved. While the calculation of 6% of 40 might seem simple at first glance, the underlying concepts form the foundation for more intricate percentage problems. By mastering the basic principles and exploring various calculation methods, you can equip yourself with a powerful tool for navigating the numerical world around you with greater confidence and efficiency.
Latest Posts
Latest Posts
-
Convert 3 93 103 From Scientific Notation To Standard Notation
May 12, 2025
-
Four To The Power Of Four
May 12, 2025
-
1 Tonne Of Sand How Many M3
May 12, 2025
-
1 And 2 3 As A Improper Fraction
May 12, 2025
-
104 Divided By 16 With Remainder
May 12, 2025
Related Post
Thank you for visiting our website which covers about What Is 6 Percent Of 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.