What Is 8/40 As A Percent
Treneri
May 12, 2025 · 5 min read
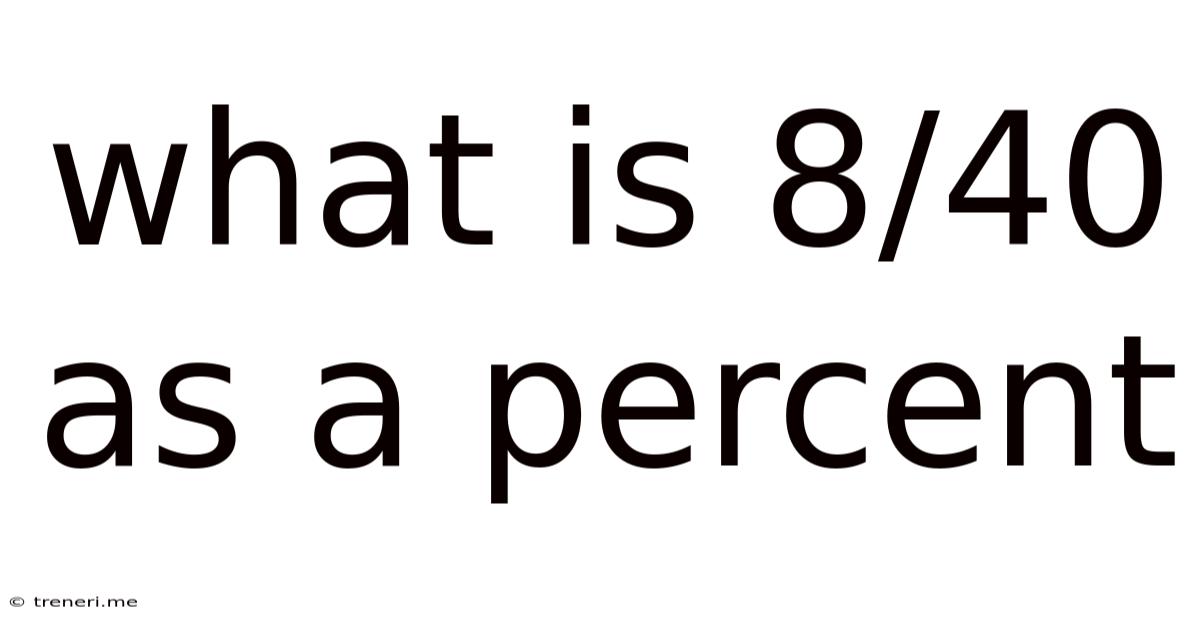
Table of Contents
What is 8/40 as a Percent? A Comprehensive Guide to Fraction-to-Percentage Conversions
Understanding how to convert fractions to percentages is a fundamental skill in mathematics with broad applications in everyday life, from calculating discounts and tips to understanding financial reports and statistical data. This comprehensive guide will delve into the process of converting the fraction 8/40 into a percentage, explaining the underlying principles and providing practical examples to solidify your understanding. We'll also explore various methods for performing this conversion, ensuring you have a versatile toolkit for tackling similar problems.
Understanding Fractions and Percentages
Before diving into the conversion, let's establish a clear understanding of the terms involved.
Fractions: A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates the number of parts you have, while the denominator indicates the total number of parts in the whole. In the fraction 8/40, 8 is the numerator and 40 is the denominator.
Percentages: A percentage is a way of expressing a number as a fraction of 100. The symbol "%" is used to represent percentage. For example, 50% means 50 out of 100, or 50/100. Percentages provide a standardized way to compare proportions and are widely used in various contexts.
Method 1: Simplifying the Fraction
The most straightforward method to convert 8/40 to a percentage involves first simplifying the fraction to its lowest terms. This makes the subsequent calculation easier.
Step 1: Find the Greatest Common Divisor (GCD)
The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder. In this case, the GCD of 8 and 40 is 8.
Step 2: Divide Both the Numerator and Denominator by the GCD
Dividing both 8 and 40 by 8, we get:
8 ÷ 8 = 1 40 ÷ 8 = 5
This simplifies the fraction 8/40 to 1/5.
Step 3: Convert the Simplified Fraction to a Percentage
To convert a fraction to a percentage, we multiply the fraction by 100%:
(1/5) * 100% = 20%
Therefore, 8/40 is equivalent to 20%.
Method 2: Direct Conversion using Division
This method involves directly dividing the numerator by the denominator and then multiplying the result by 100%.
Step 1: Divide the Numerator by the Denominator
Divide 8 by 40:
8 ÷ 40 = 0.2
Step 2: Multiply the Result by 100%
Multiply 0.2 by 100%:
0.2 * 100% = 20%
Again, we arrive at the answer: 8/40 is equal to 20%.
Method 3: Using Proportions
This method utilizes the concept of proportions to solve the problem. We can set up a proportion to find the equivalent percentage.
Step 1: Set up a Proportion
We can set up a proportion as follows:
8/40 = x/100
where 'x' represents the percentage we want to find.
Step 2: Solve for x
To solve for x, we can cross-multiply:
40x = 800
Then, divide both sides by 40:
x = 800 ÷ 40 = 20
Therefore, x = 20, meaning 8/40 is equal to 20%.
Practical Applications of Fraction-to-Percentage Conversions
The ability to convert fractions to percentages is invaluable in numerous real-world scenarios. Here are a few examples:
-
Calculating Discounts: If a store offers a 20% discount on an item, and you want to know the equivalent fractional discount, you'd convert 20% back to a fraction (20/100 = 1/5).
-
Analyzing Financial Statements: Financial reports often express data as percentages, and understanding how to convert fractions to percentages allows for better analysis of financial performance.
-
Understanding Test Scores: Test scores are frequently presented as percentages, and the ability to convert fractions helps in comparing performance against different scoring systems.
-
Statistical Analysis: Statistics often involves calculating proportions, and the ability to convert between fractions and percentages is essential for interpreting results.
-
Cooking and Baking: Recipes often involve fractions, and understanding percentages can be helpful when adjusting recipes to serve more or fewer people.
Beyond 8/40: Mastering Fraction-to-Percentage Conversions
The techniques outlined above can be applied to any fraction. The key is to understand the fundamental principles: simplifying fractions to their lowest terms, dividing the numerator by the denominator, and multiplying the result by 100% to obtain the percentage.
Remember to always double-check your work, particularly when dealing with complex fractions. Using a calculator can help with the division and multiplication steps, ensuring accuracy in your calculations.
Troubleshooting Common Mistakes
Here are some common mistakes to avoid when converting fractions to percentages:
-
Forgetting to multiply by 100%: A common error is to stop after dividing the numerator by the denominator. Remember that the result must be multiplied by 100% to express it as a percentage.
-
Incorrect simplification of fractions: Improper simplification of fractions can lead to inaccurate results. Ensure you find the greatest common divisor (GCD) to simplify the fraction effectively.
-
Decimal point errors: When dealing with decimal numbers, be careful to place the decimal point correctly in your calculations.
Conclusion
Converting 8/40 to a percentage is a straightforward process, and understanding the different methods allows for flexibility in tackling similar problems. Mastering this skill is crucial for various applications in daily life and academic pursuits. By understanding the fundamentals of fractions and percentages, and by practicing the different conversion techniques, you'll build a strong foundation for future mathematical endeavors. This skill, seemingly simple, opens doors to a deeper understanding of numerical relationships and data interpretation. Remember to practice regularly to solidify your understanding and improve your speed and accuracy.
Latest Posts
Latest Posts
-
How Many Sig Figs Is 10 0
May 14, 2025
-
Cuanto Es 15 Libras En Kg
May 14, 2025
-
Calories Burn In 10 Km Running
May 14, 2025
-
90 Days From April 1st 2024
May 14, 2025
-
How Many Seconds Are There In 10 Minutes
May 14, 2025
Related Post
Thank you for visiting our website which covers about What Is 8/40 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.