What Is 90 Percent Of 20
Treneri
Apr 14, 2025 · 5 min read
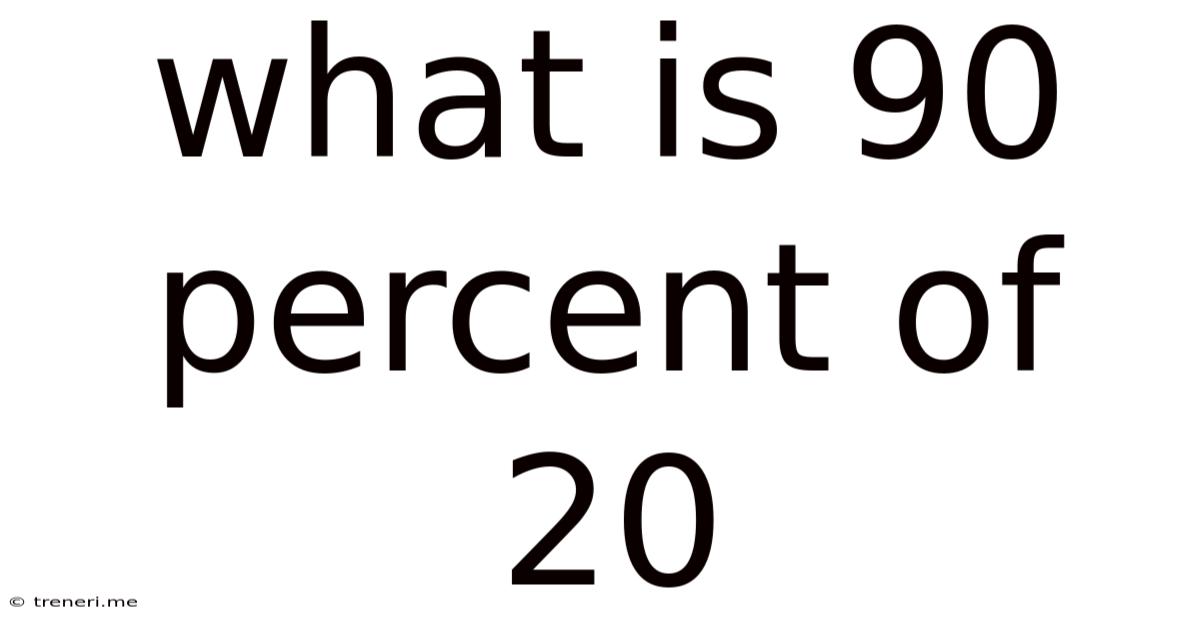
Table of Contents
What is 90 Percent of 20? A Deep Dive into Percentages and Their Applications
Finding 90 percent of 20 might seem like a simple arithmetic problem, suitable only for elementary school students. However, understanding how to calculate percentages, and the underlying concepts, is crucial across numerous fields, from everyday budgeting to complex financial modeling. This article will not only answer the question – what is 90 percent of 20? – but will also explore the broader context of percentages, their applications, and how to tackle similar problems with confidence.
Calculating 90% of 20: The Basics
The most straightforward method to calculate 90% of 20 involves converting the percentage to a decimal and then multiplying. Remember that a percentage represents a fraction out of 100. Therefore, 90% can be written as 90/100, which simplifies to 0.9.
To find 90% of 20, we simply multiply 20 by 0.9:
20 * 0.9 = 18
Therefore, 90% of 20 is 18.
This basic calculation forms the foundation for understanding more complex percentage problems.
Different Methods for Calculating Percentages
While the decimal method is the most efficient for simple calculations, other methods can be equally useful, especially when dealing with more challenging percentages or mental arithmetic:
-
Fraction Method: 90% can also be represented as the fraction 9/10. Multiplying 20 by 9/10 gives us (20 * 9) / 10 = 180 / 10 = 18. This method is helpful for understanding the relationship between percentages and fractions.
-
Proportion Method: This method sets up a proportion: 90/100 = x/20. Cross-multiplying and solving for x gives us 100x = 1800, resulting in x = 18. This method is particularly useful when dealing with more complex scenarios involving unknown variables.
-
Using a Calculator: For more intricate calculations or when speed is essential, using a calculator is the most practical approach. Simply enter 20 * 0.9 or 20 * 90% (depending on your calculator's functionality) to get the answer.
Real-World Applications of Percentage Calculations
The ability to calculate percentages extends far beyond simple arithmetic exercises. It's a fundamental skill in numerous aspects of life, including:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns all rely heavily on percentage calculations. For example, understanding the interest rate on a loan or the discount on a sale item requires a firm grasp of percentages.
-
Business: Businesses use percentages to analyze sales figures, market share, growth rates, and operational efficiency. Understanding percentage change, for instance, is crucial for tracking performance and making informed business decisions.
-
Science: In scientific research, percentages are commonly used to express data, such as the percentage of a population exhibiting a certain characteristic or the percentage change in a measured variable.
-
Everyday Life: We encounter percentages daily, from calculating tips in restaurants to understanding sale discounts in stores. The ability to quickly calculate percentages saves time and ensures accurate financial transactions.
Percentage Increase and Decrease
Beyond simply finding a percentage of a number, understanding percentage increase and decrease is also crucial. These calculations are commonly used to express changes in values over time.
Percentage Increase: This calculation determines the percentage by which a value has increased. The formula is:
[(New Value - Original Value) / Original Value] * 100%
For example, if a product's price increases from $20 to $25, the percentage increase is:
[(25 - 20) / 20] * 100% = 25%
Percentage Decrease: This calculation determines the percentage by which a value has decreased. The formula is:
[(Original Value - New Value) / Original Value] * 100%
For example, if a product's price decreases from $20 to $15, the percentage decrease is:
[(20 - 15) / 20] * 100% = 25%
Tackling More Complex Percentage Problems
While finding 90% of 20 is relatively straightforward, more complex scenarios may involve multiple percentage calculations or finding the original value based on a percentage change. Let's explore a couple of examples:
Example 1: A store offers a 20% discount on an item originally priced at $50. What is the final price after the discount?
First, calculate the discount amount: 50 * 0.20 = $10. Then, subtract the discount from the original price: 50 - 10 = $40. The final price is $40.
Example 2: After a 15% increase, a population is now 115,000. What was the original population?
Let 'x' represent the original population. We can set up the equation: x + 0.15x = 115,000. Simplifying this gives 1.15x = 115,000. Dividing both sides by 1.15 gives x = 100,000. The original population was 100,000.
Improving Your Percentage Calculation Skills
Mastering percentage calculations requires practice and a solid understanding of the underlying concepts. Here are some tips to improve your skills:
-
Practice regularly: Solve various percentage problems, ranging from simple to complex, to build your confidence and fluency.
-
Use different methods: Experiment with different calculation methods to find the approach that best suits your learning style and the problem at hand.
-
Understand the concepts: Don't just memorize formulas; strive to understand the underlying principles of percentages and their application.
-
Utilize online resources: Numerous websites and online calculators offer practice problems and explanations to further enhance your understanding.
-
Break down complex problems: Decompose complex percentage problems into smaller, more manageable steps to avoid errors and enhance clarity.
Conclusion: Beyond the Basics of 90% of 20
While the answer to "What is 90 percent of 20?" is simply 18, the journey to finding that answer highlights the importance of understanding percentage calculations. These calculations are fundamental in various fields, and mastering them empowers you to tackle more complex problems in finance, business, science, and everyday life. By practicing regularly and understanding the underlying concepts, you can build your confidence and fluency in working with percentages, transforming them from a simple arithmetic concept into a powerful tool for problem-solving. Remember to use the methods that resonate most with you, whether it's the decimal method, the fraction method, or utilizing a calculator. The key is to understand the principles and apply them consistently to achieve accurate results.
Latest Posts
Latest Posts
-
Cuanto Es 7 5 Pies En Centimetros
May 10, 2025
-
18 Km Equals How Many Miles
May 10, 2025
-
What Is Time And A Half Of 15 50
May 10, 2025
-
15 Is 40 Percent Of What
May 10, 2025
-
How To Find The Missing Dimension Of A Triangle
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Is 90 Percent Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.