What Is Five Percent Of 100
Treneri
May 10, 2025 · 5 min read
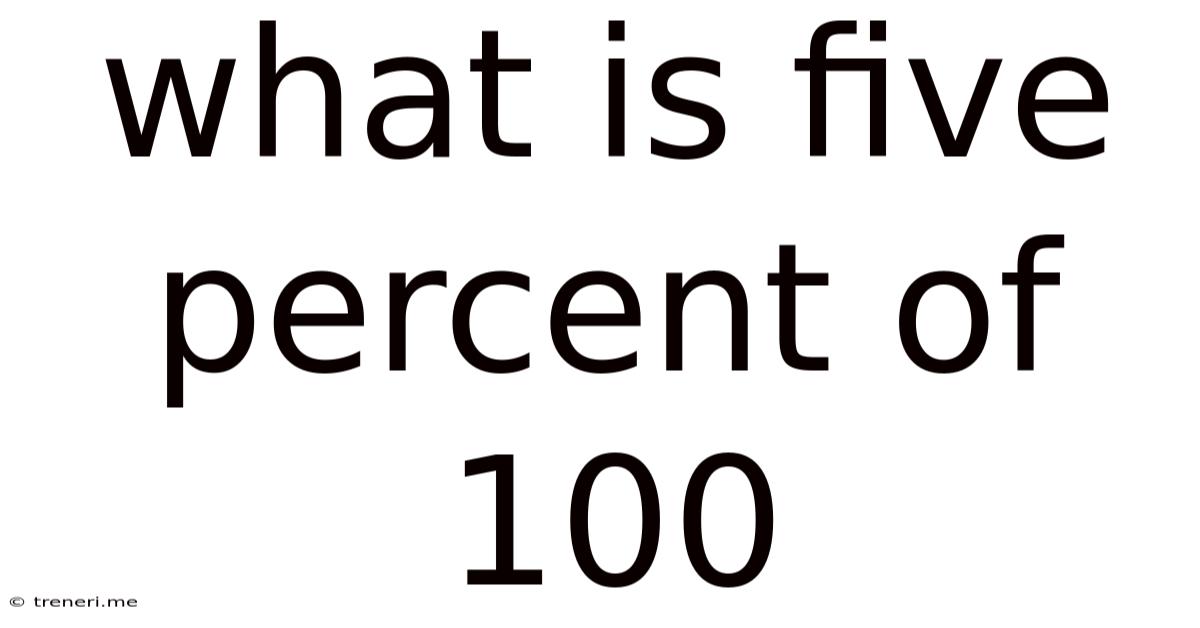
Table of Contents
What is Five Percent of 100? A Deep Dive into Percentages and Their Applications
Finding five percent of 100 might seem like a simple task, easily solved with a quick calculation. However, understanding the underlying principles of percentages is crucial for various applications, from everyday budgeting to complex financial analysis. This article will not only answer the question "What is five percent of 100?" but also explore the broader concept of percentages, their practical uses, and how to calculate them efficiently.
Understanding Percentages: The Foundation
A percentage is a fraction or a ratio expressed as a number out of 100. The term "percent" is derived from the Latin words "per centum," meaning "out of one hundred." Therefore, 5% literally means 5 out of 100, or 5/100. This fundamental understanding forms the basis for all percentage calculations.
Visualizing Percentages
Imagine a 100-unit square. Five percent of this square would represent 5 of those units. This visual representation helps to grasp the concept of percentages intuitively. Similarly, if you had 100 apples, 5% would represent 5 apples.
Converting Percentages to Decimals and Fractions
Percentages can easily be converted into decimals and fractions. To convert a percentage to a decimal, simply divide the percentage by 100. For example, 5% becomes 0.05 (5 ÷ 100 = 0.05). To convert a percentage to a fraction, express it as a fraction with a denominator of 100. So, 5% is equivalent to 5/100, which can be simplified to 1/20.
Calculating Five Percent of 100: The Simple Method
Now, let's address the core question: What is five percent of 100?
The most straightforward method is to use the formula:
Percentage × Number = Result
In this case:
5% × 100 = 5
Therefore, five percent of 100 is 5.
Alternative Calculation Methods
While the above method is the simplest, other methods can be used, particularly useful when dealing with more complex percentage calculations:
-
Using Decimals: Convert 5% to its decimal equivalent (0.05) and multiply it by 100: 0.05 × 100 = 5.
-
Using Fractions: Convert 5% to its fractional equivalent (5/100 or 1/20) and multiply it by 100: (1/20) × 100 = 5.
All three methods yield the same result: 5.
Practical Applications of Percentage Calculations
The ability to calculate percentages is essential in numerous real-world situations:
1. Financial Calculations:
- Interest Rates: Calculating interest earned on savings accounts or interest paid on loans involves percentages.
- Discounts and Sales Tax: Determining the final price of an item after a discount or adding sales tax requires percentage calculations.
- Investment Returns: Tracking investment performance and calculating returns on investment (ROI) heavily relies on percentages.
- Budgeting: Allocating a percentage of your income to different expense categories is a vital part of effective budgeting.
2. Data Analysis and Statistics:
- Data Representation: Percentages are frequently used to represent data in charts, graphs, and reports, making it easier to visualize and interpret information.
- Probability and Statistics: Percentages play a critical role in expressing probabilities and statistical results.
- Surveys and Polls: Results from surveys and polls are often presented as percentages to show the proportion of respondents who chose a particular option.
3. Everyday Life:
- Tipping: Calculating a tip in a restaurant typically involves determining a percentage of the total bill.
- Cooking and Baking: Recipes often use percentages to specify the proportion of different ingredients.
- Measurement Conversions: Converting units of measurement sometimes requires percentage calculations.
Beyond the Basics: More Complex Percentage Problems
While calculating 5% of 100 is straightforward, more complex percentage problems require a slightly different approach.
Finding the Percentage:
If you know the part and the whole, you can find the percentage using this formula:
(Part / Whole) × 100 = Percentage
For example, if 15 out of 100 students passed an exam, the percentage of students who passed is (15/100) × 100 = 15%.
Finding the Whole:
If you know the part and the percentage, you can find the whole using this formula:
(Part / Percentage) × 100 = Whole
For instance, if 10 is 20% of a number, then the number is (10/20) × 100 = 50.
Finding the Part:
If you know the whole and the percentage, you can find the part using the formula we initially introduced:
Percentage × Whole = Part
For example, to find 30% of 200, the calculation would be 0.30 × 200 = 60.
Mastering Percentages: Tips and Techniques
- Practice Regularly: The key to mastering percentage calculations is consistent practice. Work through various problems of increasing complexity.
- Use Online Calculators (Judiciously): Online percentage calculators can be helpful for checking your work, but relying on them exclusively will hinder your understanding of the underlying principles.
- Understand the Context: Always pay close attention to the context of the problem to ensure you're using the correct formula and interpreting the results accurately.
- Break Down Complex Problems: For complex problems, break them down into smaller, more manageable steps.
- Develop Mental Math Skills: With practice, you can develop the ability to estimate percentages mentally, which is a valuable skill in many situations.
Conclusion: The Power of Percentage Understanding
Understanding percentages is a fundamental skill applicable across numerous fields and everyday scenarios. While calculating five percent of 100 might seem trivial, mastering the underlying concepts empowers you to tackle more complex percentage problems with confidence. By consistently practicing and applying these techniques, you can significantly improve your mathematical abilities and enhance your problem-solving skills in various aspects of life. Remember, the seemingly simple question "What is five percent of 100?" opens a door to a world of numerical understanding and practical application.
Latest Posts
Latest Posts
-
62 Inches Is How Many Meters
May 10, 2025
-
10 Days In Hours Minutes And Seconds
May 10, 2025
-
What Is The Equivalent Fraction Of 2 6
May 10, 2025
-
What Is Square Root Of 70
May 10, 2025
-
What Is The Lcm Of 6 8 And 9
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Is Five Percent Of 100 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.