What Is The Distance Between 6 8 And 3 9
Treneri
May 10, 2025 · 5 min read
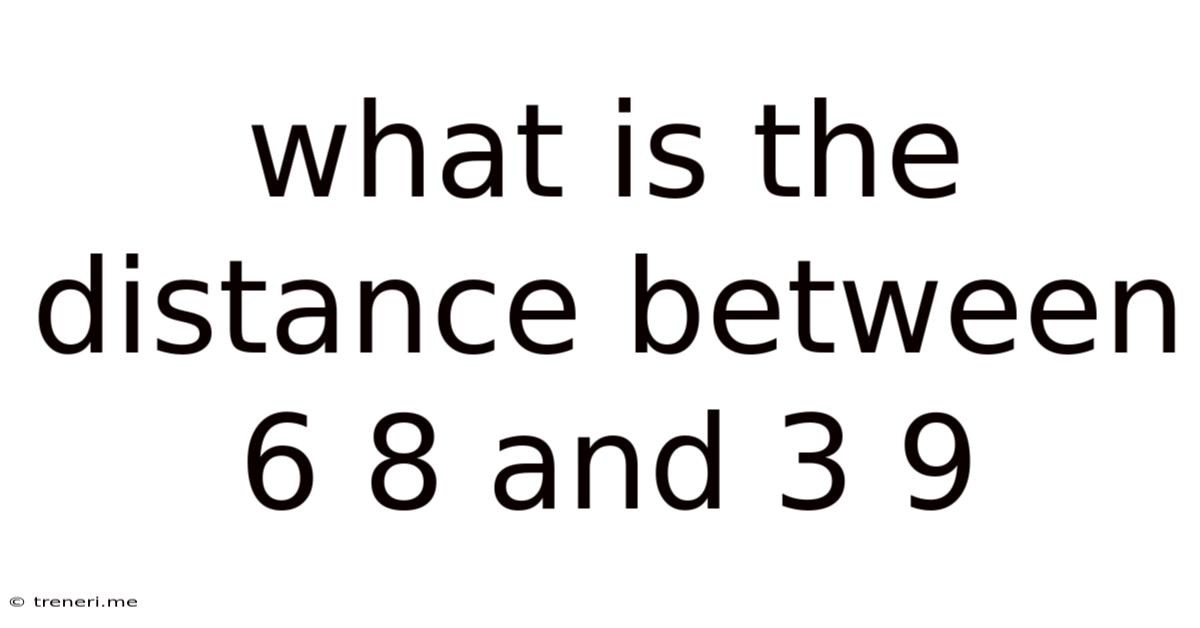
Table of Contents
What is the Distance Between (6, 8) and (3, 9)? A Comprehensive Guide to Distance Calculations
Determining the distance between two points is a fundamental concept in mathematics with wide-ranging applications in various fields, from computer graphics and navigation to physics and engineering. This article delves into the calculation of the distance between the points (6, 8) and (3, 9), explaining the underlying principles and providing a comprehensive understanding of distance formulas. We'll also explore the broader context of distance calculations and their significance.
Understanding Coordinate Systems
Before we embark on the distance calculation, it's crucial to understand the coordinate system we're working within. The points (6, 8) and (3, 9) are represented in a two-dimensional Cartesian coordinate system. This system uses two perpendicular lines, the x-axis (horizontal) and the y-axis (vertical), to define the location of any point on a plane. Each point is identified by its x-coordinate (the horizontal position) and its y-coordinate (the vertical position).
In our example:
- (6, 8) means a point located 6 units along the x-axis and 8 units along the y-axis.
- (3, 9) means a point located 3 units along the x-axis and 9 units along the y-axis.
Applying the Distance Formula
The most common method to find the distance between two points (x₁, y₁) and (x₂, y₂) in a Cartesian coordinate system is using the distance formula, which is derived from the Pythagorean theorem. The formula is:
d = √[(x₂ - x₁)² + (y₂ - y₁)²]
Where:
- d represents the distance between the two points.
- x₁ and y₁ are the coordinates of the first point.
- x₂ and y₂ are the coordinates of the second point.
Calculating the Distance Between (6, 8) and (3, 9)
Let's apply the distance formula to calculate the distance between (6, 8) and (3, 9):
-
Identify the coordinates:
- (x₁, y₁) = (6, 8)
- (x₂, y₂) = (3, 9)
-
Substitute the coordinates into the distance formula: d = √[(3 - 6)² + (9 - 8)²]
-
Simplify the equation: d = √[(-3)² + (1)²] d = √[9 + 1] d = √10
-
Calculate the final distance: d ≈ 3.162
Therefore, the distance between the points (6, 8) and (3, 9) is approximately 3.162 units.
Visualizing the Distance
It's helpful to visualize this calculation. Imagine a right-angled triangle formed by the two points and a horizontal or vertical line connecting them. The horizontal distance is the difference in x-coordinates (|3 - 6| = 3), and the vertical distance is the difference in y-coordinates (|9 - 8| = 1). The distance between the two points is the hypotenuse of this right-angled triangle, calculated using the Pythagorean theorem (a² + b² = c²), which is the basis of the distance formula.
Applications of Distance Calculations
The seemingly simple act of calculating the distance between two points has far-reaching applications in numerous fields:
1. Mapping and Navigation:
GPS systems rely heavily on distance calculations to determine the shortest routes between locations, calculate travel times, and provide accurate directions. Mapping applications use these calculations to display distances between points on a map.
2. Computer Graphics:
In computer graphics and game development, distance calculations are essential for rendering images, detecting collisions between objects, and implementing realistic physics simulations. Determining the distance between objects helps the computer determine which objects are closer to the viewer and should be rendered with higher detail.
3. Physics and Engineering:
Distance calculations play a vital role in physics and engineering. They are crucial in calculating forces, velocities, and accelerations in various scenarios, including projectile motion, orbital mechanics, and structural analysis.
4. Data Analysis and Machine Learning:
In data analysis and machine learning, distance calculations are used in clustering algorithms (like k-means clustering), which group similar data points together based on their proximity. This technique is widely used in various applications, including image recognition, customer segmentation, and anomaly detection.
5. Network Analysis:
In network analysis, distance calculations are crucial in determining the shortest path between nodes in a network. This has applications in various fields, including social network analysis, transportation networks, and computer networks.
Beyond Two Dimensions: Extending the Concept
The distance formula we've discussed applies to two-dimensional space. However, the concept of distance can be extended to higher dimensions. For three-dimensional space, the distance formula becomes:
d = √[(x₂ - x₁)² + (y₂ - y₁)² + (z₂ - z₁)²]
Where (x₁, y₁, z₁) and (x₂, y₂, z₂) represent the coordinates of the two points in three-dimensional space. This can be further generalized to n-dimensional space.
Conclusion: The Significance of Simple Calculations
The calculation of the distance between two points, although seemingly straightforward, underlies a vast array of complex applications. Understanding the distance formula and its implications is essential for anyone working in fields involving spatial relationships, data analysis, or any discipline that relies on the accurate representation and manipulation of coordinates. From navigating our world to building complex computer systems, the simple concept of distance holds a key position in numerous technological and scientific advancements. Mastering this fundamental calculation provides a robust foundation for tackling more advanced mathematical concepts and their real-world applications. The seemingly small distance of approximately 3.162 units between (6, 8) and (3, 9) represents much more than just a numerical value; it signifies the power of simple mathematical principles in shaping our understanding and interaction with the world around us.
Latest Posts
Latest Posts
-
How To Know How Much Muscle You Have
May 11, 2025
-
What Is A 1 4 Oz In Grams
May 11, 2025
-
How Many Km Is 30 Minutes Driving
May 11, 2025
-
Cuanto Es 80 Gramos En Cucharadas
May 11, 2025
-
41 8 As A Mixed Number
May 11, 2025
Related Post
Thank you for visiting our website which covers about What Is The Distance Between 6 8 And 3 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.