What Is The Gcf Of 10 And 12
Treneri
May 15, 2025 · 5 min read
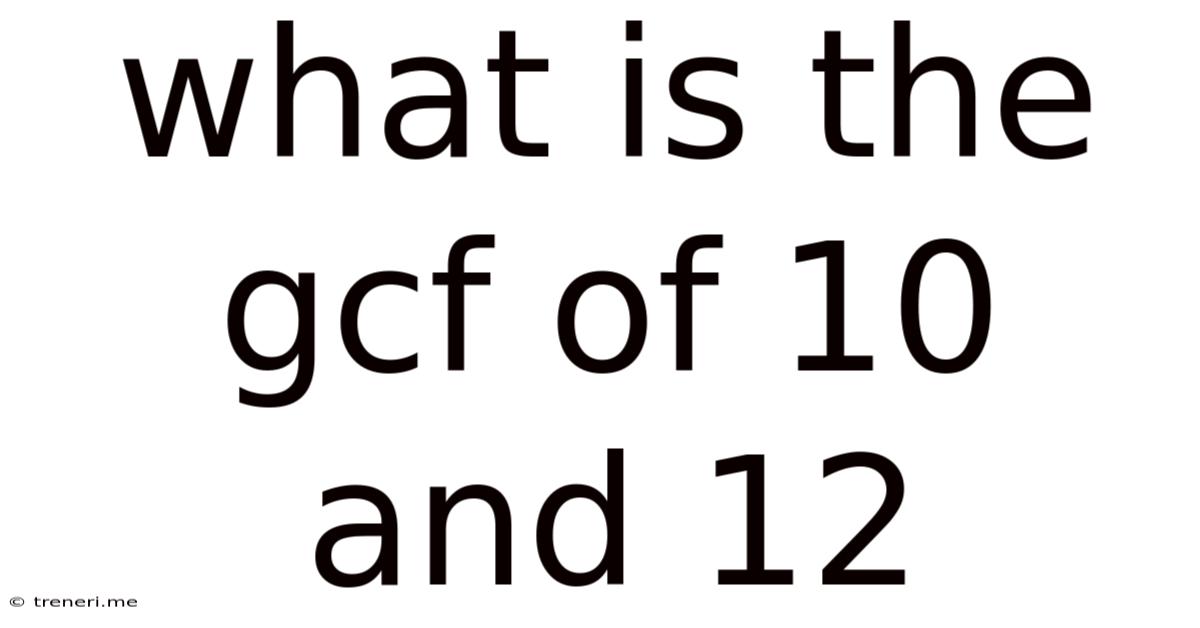
Table of Contents
What is the GCF of 10 and 12? A Deep Dive into Greatest Common Factors
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts and various methods for calculating it is crucial for a strong foundation in mathematics. This comprehensive guide will not only answer the question "What is the GCF of 10 and 12?" but will also delve into the broader world of GCFs, exploring different approaches and their applications.
Understanding Greatest Common Factors (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers evenly. This concept is fundamental in various mathematical fields, including algebra, number theory, and cryptography.
Why are GCFs Important?
GCFs aren't just abstract mathematical concepts; they have practical applications:
-
Simplifying Fractions: Finding the GCF allows us to simplify fractions to their lowest terms. For instance, to simplify 12/18, finding the GCF (which is 6) lets us reduce the fraction to 2/3.
-
Solving Equations: GCFs play a crucial role in solving algebraic equations and simplifying expressions.
-
Geometry and Measurement: GCFs are used in problems involving geometric shapes and measurements, helping determine the largest possible size of identical squares or tiles that can perfectly cover a given area.
-
Number Theory: GCFs are a cornerstone of number theory, a branch of mathematics that studies the properties of integers.
Methods for Finding the GCF of 10 and 12
Let's now tackle the specific question: What is the GCF of 10 and 12? We'll explore several methods to find the solution.
1. Listing Factors
This method involves listing all the factors of each number and then identifying the largest common factor.
Factors of 10: 1, 2, 5, 10 Factors of 12: 1, 2, 3, 4, 6, 12
Comparing the lists, we see that the common factors are 1 and 2. The largest of these is 2.
Therefore, the GCF of 10 and 12 is 2.
2. Prime Factorization
This method utilizes the prime factorization of each number. Prime factorization involves expressing a number as a product of its prime factors (numbers divisible only by 1 and themselves).
Prime factorization of 10: 2 x 5 Prime factorization of 12: 2 x 2 x 3 (or 2² x 3)
The common prime factor is 2. Therefore, the GCF is 2. This method is particularly useful for larger numbers.
3. Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the GCF of two numbers, especially when dealing with larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal.
Let's apply it to 10 and 12:
- 12 = 10 x 1 + 2 (12 - 10 = 2)
- 10 = 2 x 5 + 0 (10 - 2 x 5 =0)
Since the remainder is 0, the GCF is the last non-zero remainder, which is 2.
4. Using a GCF Calculator (for demonstration purposes only)
While it's important to understand the underlying mathematical principles, online GCF calculators can be useful for verification or when dealing with very large numbers. Remember, the focus should be on understanding the methods, not solely relying on calculators.
Expanding the Understanding of GCFs
Now that we've established the GCF of 10 and 12, let's broaden our perspective on GCFs.
GCF of More Than Two Numbers
The concept of GCF extends to more than two numbers. To find the GCF of multiple numbers, you can use any of the methods described above, applying them iteratively. For example, to find the GCF of 10, 12, and 15:
-
Prime Factorization:
- 10 = 2 x 5
- 12 = 2² x 3
- 15 = 3 x 5
The only common prime factor is none, so the GCF is 1.
-
Euclidean Algorithm (Iterative): This method becomes more complex with multiple numbers, often requiring repeated application of the algorithm.
Least Common Multiple (LCM) and its Relationship to GCF
The least common multiple (LCM) is the smallest positive integer that is a multiple of each of the given integers. There's a significant relationship between the GCF and LCM of two numbers (a and b):
LCM(a, b) x GCF(a, b) = a x b
For 10 and 12:
- GCF(10, 12) = 2
- LCM(10, 12) = 60
2 x 60 = 120 = 10 x 12. This formula provides a way to calculate the LCM if you already know the GCF, or vice-versa.
Advanced Concepts and Applications
The concept of GCF has far-reaching implications in advanced mathematical areas.
Modular Arithmetic and Cryptography
GCFs play a critical role in modular arithmetic, which forms the basis of many cryptographic systems. The Euclidean algorithm is often used to find modular inverses, which are essential in public-key cryptography.
Abstract Algebra
In abstract algebra, the concept of GCF generalizes to the notion of greatest common divisor in rings and ideals. This area deals with more abstract mathematical structures than just integers.
Applications in Computer Science
GCFs are used in various computer science algorithms, including those related to data compression and graph theory.
Conclusion: Mastering GCFs for Mathematical Proficiency
Understanding the greatest common factor is not merely about finding the largest number that divides two integers without a remainder. It represents a fundamental concept that underpins numerous mathematical operations and applications. By mastering the various methods for calculating GCFs—listing factors, prime factorization, and the Euclidean algorithm—you'll strengthen your mathematical foundation and gain valuable skills applicable in various fields. Remember that the choice of method depends on the context and the size of the numbers involved. For small numbers, listing factors is straightforward, but for larger numbers, prime factorization or the Euclidean algorithm prove more efficient. The consistent practice of these methods will enhance your mathematical comprehension and problem-solving abilities. The journey to mastering GCFs is not just about the answer; it's about the understanding and the process.
Latest Posts
Latest Posts
-
88 83 Is What Percent Of 21
May 15, 2025
-
Cuantas Semanas Tiene Un Ano De 365 Dias
May 15, 2025
-
How Many Ounce In A Kilogram
May 15, 2025
-
How Many Cubic Feet Is 55 Quarts Of Potting Soil
May 15, 2025
-
What Is The Gcf For 18 And 32
May 15, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 10 And 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.