What Is The Gcf Of 18 And 35
Treneri
May 12, 2025 · 5 min read
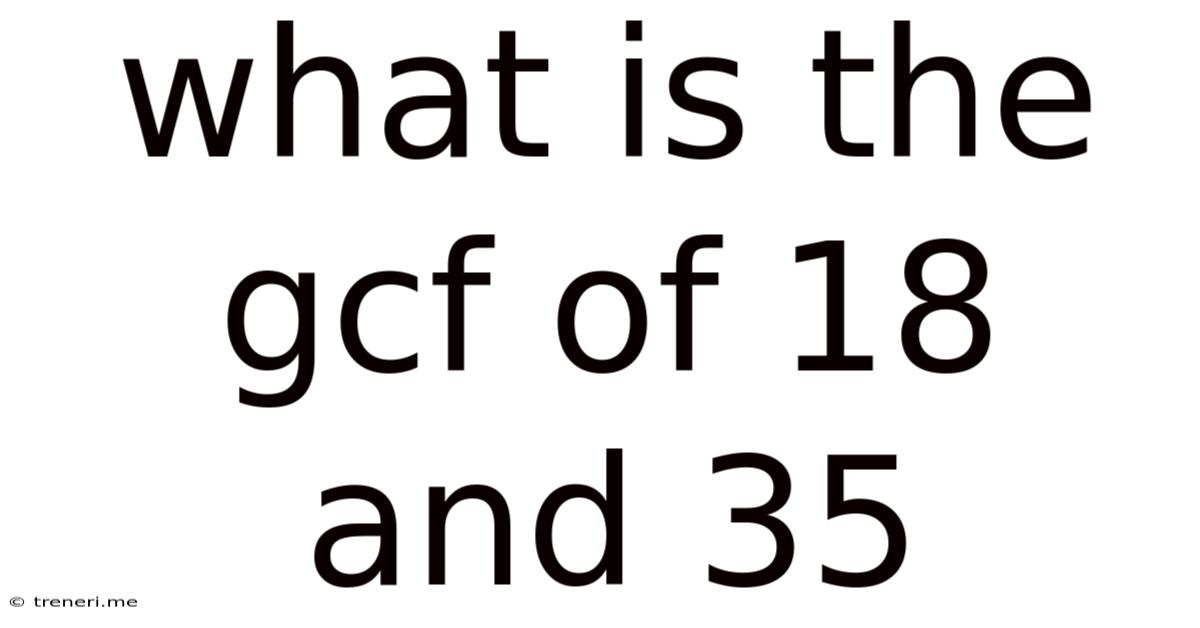
Table of Contents
What is the GCF of 18 and 35? A Deep Dive into Greatest Common Factor
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic problem, but understanding the underlying concepts and different methods for solving it is crucial for various mathematical applications. This article will thoroughly explore how to find the GCF of 18 and 35, delving into the meaning of GCF, various calculation methods, and its broader significance in mathematics and beyond.
Understanding Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers evenly. Understanding this definition is the foundation for finding the GCF of any pair of numbers, including 18 and 35.
Why is finding the GCF important?
The concept of GCF has widespread applications across various mathematical fields and practical scenarios:
- Simplifying Fractions: GCF is essential for simplifying fractions to their lowest terms. By dividing both the numerator and denominator by their GCF, you obtain an equivalent fraction in its simplest form.
- Algebraic Simplification: In algebra, GCF plays a crucial role in factoring expressions, making them easier to solve or analyze.
- Problem Solving: Many real-world problems involving division or sharing require finding the GCF to distribute items evenly or solve problems related to measurement and geometry.
- Number Theory: GCF is a fundamental concept in number theory, forming the basis for understanding more complex number relationships.
Methods for Finding the GCF of 18 and 35
Several methods exist for calculating the GCF of two numbers. Let's explore the most common approaches and apply them to find the GCF of 18 and 35:
1. Listing Factors Method
This method involves listing all the factors of each number and then identifying the largest common factor.
Factors of 18: 1, 2, 3, 6, 9, 18 Factors of 35: 1, 5, 7, 35
Comparing the two lists, we see that the only common factor is 1.
Therefore, the GCF of 18 and 35 is 1.
2. Prime Factorization Method
This is a more systematic approach, particularly useful for larger numbers. It involves breaking down each number into its prime factors and then identifying the common prime factors raised to the lowest power.
Prime Factorization of 18: 2 x 3 x 3 = 2 x 3² Prime Factorization of 35: 5 x 7
Since there are no common prime factors between 18 and 35, their GCF is 1.
3. Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the GCF, especially for larger numbers. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 18 and 35:
- 35 - 18 = 17
- 18 - 17 = 1
- 17 - 16 = 1
We continue this process until we reach a remainder of 0. In this case, when we reach 1, the next step would be 17-16=1, repeating this process demonstrates that the greatest common divisor is 1.
Therefore, the GCF of 18 and 35 is 1.
Relatively Prime Numbers
When the GCF of two numbers is 1, as is the case with 18 and 35, the numbers are called relatively prime or coprime. This means they share no common factors other than 1. This property is significant in various mathematical contexts, especially in number theory.
Expanding on the Concept of GCF
The concept of GCF extends beyond just two numbers. You can find the GCF of three or more numbers using the same principles. For instance, if you wanted to find the GCF of 18, 35, and 21, you would first find the GCF of 18 and 35 (which is 1), and then find the GCF of that result (1) and 21, which would also be 1.
Applications of GCF in Real-World Scenarios
While the GCF might seem like an abstract mathematical concept, it has several practical applications:
-
Sharing Items: Imagine you have 18 apples and 35 oranges. If you want to divide them into equal groups without having any leftover fruits, the GCF will tell you the maximum number of groups you can make (which is 1 group in this case, since 18 and 35 are coprime).
-
Measurement Conversions: When converting units of measurement, GCF helps simplify ratios.
-
Tiling and Pattern Design: In design and construction, GCF can assist in finding the largest common tile size to fit a specific area.
-
Scheduling and Timing: GCF can be used to determine the time intervals when certain events coincide, like two cyclical processes repeating at different rates.
Conclusion: The Significance of GCF
Finding the GCF of 18 and 35, which is 1, highlights the importance of understanding this fundamental mathematical concept. Whether using the listing factors method, prime factorization, or the Euclidean algorithm, the process reveals not only the GCF itself but also underscores the principles of divisibility, prime numbers, and number relationships. The applications of GCF extend far beyond simple arithmetic, providing a crucial tool for solving problems and simplifying calculations in various mathematical and practical scenarios. The understanding of GCF is fundamental for students and professionals alike. Its significance lies in its ability to simplify complex problems and facilitate a deeper understanding of number theory and its applications in the real world. The seemingly simple question, "What is the GCF of 18 and 35?" opens up a world of mathematical exploration and understanding.
Latest Posts
Latest Posts
-
21 Pounds Equals How Many Ounces
May 12, 2025
-
Is 5 A Good Uv Index To Tan
May 12, 2025
-
Greatest Common Factor Of 26 And 36
May 12, 2025
-
6 9 Kg To Lbs And Oz
May 12, 2025
-
Four To The Power Of Three
May 12, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 18 And 35 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.