What Is The Gcf Of 21 And 40
Treneri
May 11, 2025 · 5 min read
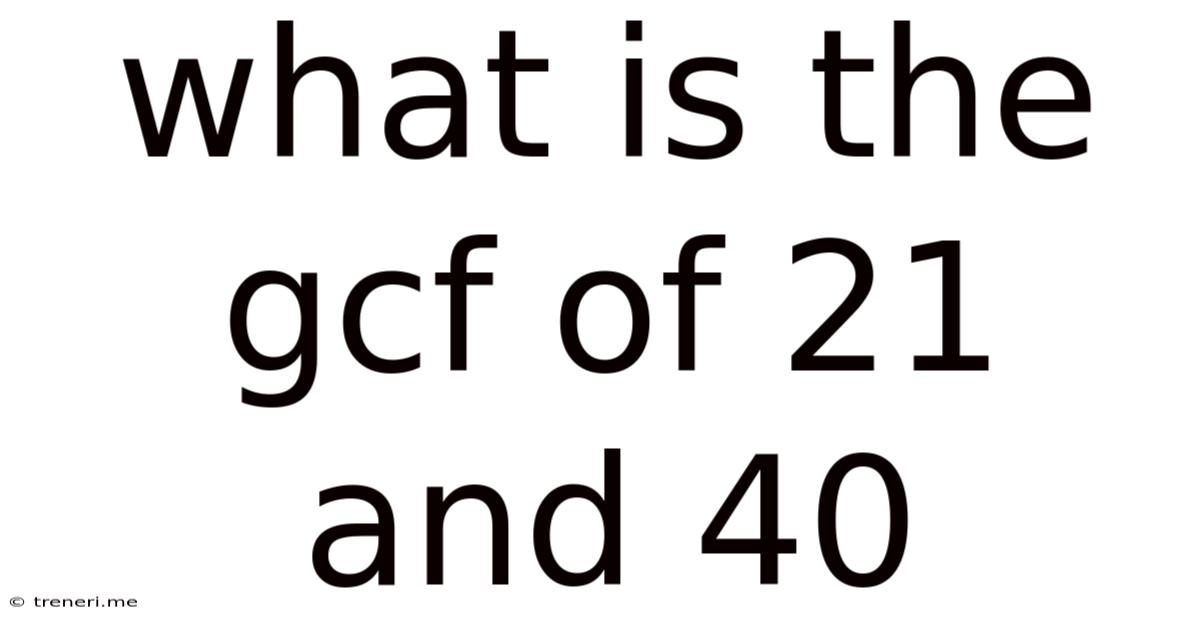
Table of Contents
What is the GCF of 21 and 40? A Deep Dive into Greatest Common Factors
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts and different methods for calculating it opens up a world of mathematical understanding. This article will not only answer the question, "What is the GCF of 21 and 40?" but will also delve into the broader world of number theory, exploring various techniques and their applications. We'll explore the significance of GCFs beyond simple arithmetic, examining their role in algebra, geometry, and even computer science.
Understanding Greatest Common Factors (GCF)
Before we tackle the specific case of 21 and 40, let's establish a solid foundation. The greatest common factor (GCF), also known as the greatest common divisor (GCD), of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers perfectly.
Example: The GCF of 12 and 18 is 6 because 6 is the largest number that divides both 12 and 18 evenly.
Why are GCFs important? They're fundamental in simplifying fractions, solving algebraic equations, and understanding the relationships between numbers. They are the building blocks of many more complex mathematical concepts.
Method 1: Prime Factorization
This is arguably the most common and conceptually straightforward method for finding the GCF. It involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
Steps:
-
Find the prime factorization of each number. This means expressing each number as a product of prime numbers.
-
Identify common prime factors. Look for the prime numbers that appear in both factorizations.
-
Multiply the common prime factors. The product of these common prime factors is the GCF.
Let's apply this method to find the GCF of 21 and 40:
1. Prime Factorization:
- 21 = 3 x 7
- 40 = 2 x 2 x 2 x 5 = 2³ x 5
2. Common Prime Factors:
There are no common prime factors between 21 and 40. 21 only has 3 and 7 as prime factors, while 40 has 2 and 5.
3. Calculate the GCF:
Since there are no common prime factors, the GCF of 21 and 40 is 1.
Method 2: Listing Factors
This method is simpler for smaller numbers and provides a good visual understanding of factors.
Steps:
-
List all the factors of each number. Factors are numbers that divide the given number without leaving a remainder.
-
Identify common factors. Look for the numbers that appear in both lists.
-
Select the greatest common factor. The largest number among the common factors is the GCF.
Let's apply this method to 21 and 40:
1. Factors of 21: 1, 3, 7, 21
2. Factors of 40: 1, 2, 4, 5, 8, 10, 20, 40
3. Common Factors: The only common factor is 1.
4. GCF: Therefore, the GCF of 21 and 40 is 1.
Method 3: Euclidean Algorithm
This method is particularly efficient for larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers become equal, and that number is the GCF.
Steps:
-
Subtract the smaller number from the larger number.
-
Replace the larger number with the result.
-
Repeat steps 1 and 2 until the two numbers are equal. This equal number is the GCF.
Let's use the Euclidean Algorithm for 21 and 40:
- 40 - 21 = 19
- 21 - 19 = 2
- 19 - 2 - 2 - 2 - 2 - 2 - 2 - 2 - 2 = 19 - 16 = 3
- 2 - 1 = 1
- 2 - 1 = 1
This process requires repeated subtraction. A more efficient approach within the Euclidean Algorithm is to use division with remainder. We divide the larger number by the smaller number and find the remainder. Then, we replace the larger number with the smaller number and the smaller number with the remainder. We repeat this until the remainder is 0. The last non-zero remainder is the GCF.
40 ÷ 21 = 1 with a remainder of 19 21 ÷ 19 = 1 with a remainder of 2 19 ÷ 2 = 9 with a remainder of 1 2 ÷ 1 = 2 with a remainder of 0
The last non-zero remainder is 1, therefore, the GCF of 21 and 40 is 1.
Applications of GCF
The seemingly simple concept of the greatest common factor has far-reaching applications in various branches of mathematics and beyond:
-
Simplifying Fractions: The GCF is crucial for simplifying fractions to their lowest terms. Dividing both the numerator and denominator by their GCF reduces the fraction to its simplest form.
-
Algebra: GCF is used in factoring algebraic expressions. Factoring out the GCF simplifies expressions and makes solving equations easier.
-
Geometry: GCF plays a role in geometric problems involving ratios and proportions.
-
Computer Science: GCF is used in cryptography and computer algorithms.
Conclusion: The GCF of 21 and 40 is 1
Through three distinct methods – prime factorization, listing factors, and the Euclidean algorithm – we've definitively shown that the greatest common factor of 21 and 40 is 1. This seemingly simple calculation highlights the fundamental importance of understanding number theory and its applications across various mathematical fields. Mastering the calculation of GCFs is a stepping stone to tackling more complex mathematical challenges. The techniques discussed here provide a robust foundation for understanding and solving problems involving GCFs, irrespective of the size of the numbers involved. Remember to choose the method that best suits your needs and the complexity of the problem at hand.
Latest Posts
Latest Posts
-
Greatest Common Factor Of 15 And 6
May 11, 2025
-
The Average Mass Of All The Isotopes Of An Element
May 11, 2025
-
How Many Square Feet In A 4x8 Sheet Of Plywood
May 11, 2025
-
What Is 10000 Km In Miles
May 11, 2025
-
77 Out Of 80 As A Percentage
May 11, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 21 And 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.