What Is The Gcf Of 24 And 44
Treneri
May 12, 2025 · 5 min read
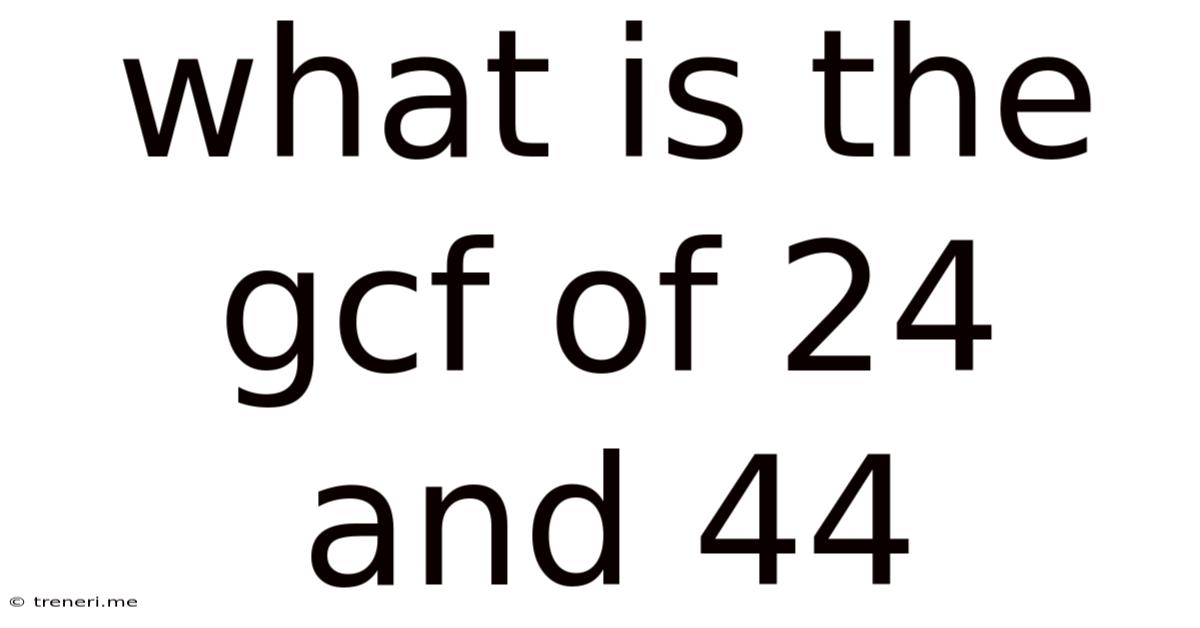
Table of Contents
What is the GCF of 24 and 44? A Deep Dive into Greatest Common Factors
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying principles and exploring different methods can unlock a deeper appreciation of number theory and its applications. This comprehensive guide will not only answer the question, "What is the GCF of 24 and 44?" but will also equip you with the knowledge to solve similar problems efficiently and effectively. We'll explore various methods, delve into the theoretical background, and even discuss real-world applications of finding GCFs.
Understanding Greatest Common Factors (GCF)
Before we tackle the specific problem of finding the GCF of 24 and 44, let's establish a firm understanding of what a GCF actually is. The greatest common factor (also known as the greatest common divisor or GCD) of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers evenly.
For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors of 12 and 18 are 1, 2, 3, and 6. Therefore, the greatest common factor of 12 and 18 is 6.
Method 1: Listing Factors
The most straightforward method for finding the GCF of smaller numbers is to list all the factors of each number and then identify the largest common factor. Let's apply this to 24 and 44:
Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24 Factors of 44: 1, 2, 4, 11, 22, 44
Comparing the two lists, we see that the common factors are 1, 2, and 4. The greatest of these common factors is 4.
Therefore, the GCF of 24 and 44 is 4.
This method is simple and intuitive, but it becomes less efficient as the numbers get larger. Imagine trying to list all the factors of 144 and 288!
Method 2: Prime Factorization
A more efficient method, especially for larger numbers, involves prime factorization. Prime factorization is the process of expressing a number as a product of its prime factors (numbers divisible only by 1 and themselves).
Let's find the prime factorization of 24 and 44:
24 = 2 x 2 x 2 x 3 = 2³ x 3 44 = 2 x 2 x 11 = 2² x 11
To find the GCF using prime factorization, we identify the common prime factors and their lowest powers. Both 24 and 44 have 2 as a common prime factor. The lowest power of 2 present in both factorizations is 2².
Therefore, the GCF of 24 and 44 is 2² = 4.
This method is significantly more efficient than listing factors, especially for larger numbers. It's a fundamental technique in number theory with widespread applications.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, especially large ones. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 24 and 44:
- 44 = 24 x 1 + 20 (Subtract 24 from 44, leaving a remainder of 20)
- 24 = 20 x 1 + 4 (Subtract 20 from 24, leaving a remainder of 4)
- 20 = 4 x 5 + 0 (Subtract multiples of 4 from 20 until the remainder is 0)
The last non-zero remainder is 4, which is the GCF of 24 and 44.
The Euclidean algorithm is remarkably efficient and forms the basis of many advanced algorithms in computer science and cryptography.
Why Understanding GCF Matters
The seemingly simple act of finding the GCF has far-reaching applications across various fields:
-
Simplification of Fractions: Finding the GCF is crucial for simplifying fractions to their lowest terms. For example, the fraction 24/44 can be simplified to 6/11 by dividing both the numerator and the denominator by their GCF, which is 4.
-
Solving Word Problems: Many real-world problems involve finding the greatest common factor. For instance, determining the largest square tiles that can perfectly cover a rectangular floor of dimensions 24 feet by 44 feet requires finding the GCF of 24 and 44.
-
Number Theory and Cryptography: GCF is a fundamental concept in number theory and plays a vital role in cryptographic algorithms that secure online transactions and communications. The Euclidean algorithm, used to find the GCF, is a cornerstone of many encryption methods.
-
Geometry and Measurement: GCF is used in geometry to solve problems involving lengths, areas, and volumes. For example, finding the greatest common divisor of the dimensions of a rectangular prism can help determine the largest possible cube that can evenly divide the prism.
-
Music Theory: GCF finds unexpected applications in music theory. For instance, identifying the GCF of note intervals can reveal harmonic relationships between different musical notes.
Beyond the Basics: Extending the Concept
The GCF concept extends beyond just two numbers. You can find the GCF of three or more numbers using the same methods. For example, to find the GCF of 24, 44, and 36, you can use prime factorization or the Euclidean algorithm repeatedly. The prime factorization of these numbers are:
- 24 = 2³ x 3
- 44 = 2² x 11
- 36 = 2² x 3²
The common prime factor is 2, and its lowest power is 2². Therefore, the GCF of 24, 44, and 36 is 4.
Conclusion: Mastering GCF Calculations
This comprehensive guide has explored various methods for finding the greatest common factor, emphasizing the importance of understanding the underlying principles. From the simple method of listing factors to the highly efficient Euclidean algorithm, we've covered multiple approaches suitable for different scenarios. Furthermore, we've highlighted the practical applications of GCF in diverse fields, demonstrating that this seemingly basic arithmetic concept plays a crucial role in advanced mathematics, computer science, and even music theory. Remember, mastering GCF calculation isn't just about solving problems; it's about building a strong foundation in number theory and appreciating its widespread relevance. So, next time you encounter a problem involving GCF, you'll be well-equipped to tackle it with confidence and efficiency.
Latest Posts
Latest Posts
-
24 Inches By 24 Inches In Square Feet
May 14, 2025
-
1 2 Cubic Yard To Square Feet
May 14, 2025
-
How Many Years Is 125 Months
May 14, 2025
-
Subtract The Quotient Of 70 Divided By 2 From 60
May 14, 2025
-
How Much Hours Is 100 Days
May 14, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 24 And 44 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.