What Is The Gcf Of 24 And 84
Treneri
May 10, 2025 · 6 min read
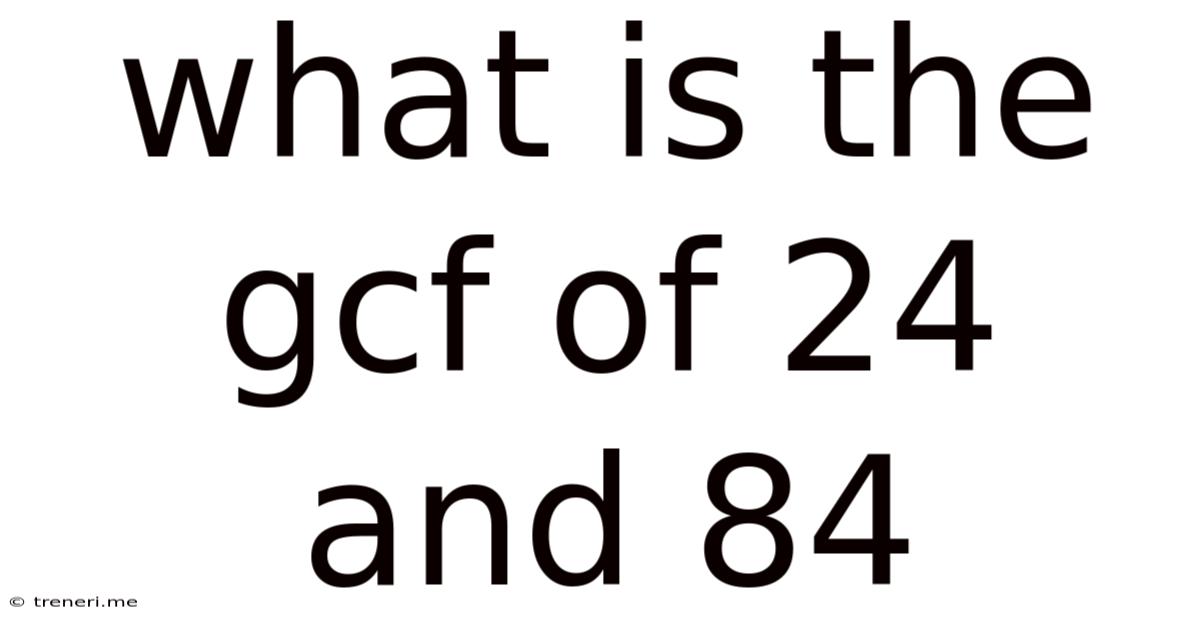
Table of Contents
What is the GCF of 24 and 84? A Deep Dive into Finding the Greatest Common Factor
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts and different methods can be incredibly valuable, especially in algebra and higher-level mathematics. This comprehensive guide will not only answer the question, "What is the GCF of 24 and 84?" but will also equip you with the knowledge and skills to tackle similar problems with confidence. We'll explore multiple methods, discuss their advantages and disadvantages, and delve into the practical applications of finding the GCF.
Understanding the Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest number that divides exactly into two or more numbers without leaving a remainder. It's a fundamental concept in number theory and has numerous applications in various fields.
Let's break down the key terms:
-
Factor: A factor of a number is a whole number that divides the number evenly (without a remainder). For example, the factors of 12 are 1, 2, 3, 4, 6, and 12.
-
Common Factor: A common factor is a factor that is shared by two or more numbers. For instance, the common factors of 12 and 18 are 1, 2, 3, and 6.
-
Greatest Common Factor (GCF): The GCF is simply the largest of these common factors. In the case of 12 and 18, the GCF is 6.
Method 1: Prime Factorization
This is arguably the most fundamental method for finding the GCF. It involves breaking down each number into its prime factors – the smallest prime numbers that multiply to give the original number.
Steps:
-
Find the prime factorization of each number. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself (e.g., 2, 3, 5, 7, 11...). We can use factor trees or other methods to achieve this.
-
Identify common prime factors. Look for the prime factors that appear in the prime factorization of both numbers.
-
Multiply the common prime factors. The product of these common prime factors is the GCF.
Let's apply this to find the GCF of 24 and 84:
Prime Factorization of 24:
24 = 2 × 2 × 2 × 3 = 2³ × 3
Prime Factorization of 84:
84 = 2 × 2 × 3 × 7 = 2² × 3 × 7
Common Prime Factors: 2 and 3 appear in both factorizations.
GCF: 2 × 2 × 3 = 12
Therefore, the GCF of 24 and 84 is $\boxed{12}$.
Advantages of Prime Factorization:
- Conceptual Understanding: This method provides a clear understanding of the underlying concept of factors and prime numbers.
- Works for any number of numbers: You can easily extend this method to find the GCF of three or more numbers.
Disadvantages of Prime Factorization:
- Can be time-consuming for large numbers: Finding the prime factorization of very large numbers can be computationally intensive.
Method 2: Listing Factors
This method involves listing all the factors of each number and then identifying the largest common factor.
Steps:
-
List all factors of each number. Remember that 1 and the number itself are always factors.
-
Identify common factors. Look for the factors that appear in both lists.
-
Find the greatest common factor. Select the largest number from the list of common factors.
Let's apply this to find the GCF of 24 and 84:
Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
Factors of 84: 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84
Common Factors: 1, 2, 3, 4, 6, 12
GCF: 12
Therefore, the GCF of 24 and 84 is $\boxed{12}$.
Advantages of Listing Factors:
- Simple and intuitive: This is a straightforward method, particularly suitable for smaller numbers.
Disadvantages of Listing Factors:
- Time-consuming for large numbers: Listing all factors for large numbers becomes impractical.
- Prone to errors: It's easy to miss factors, especially for larger numbers.
Method 3: Euclidean Algorithm
This is an efficient algorithm for finding the GCF of two numbers, particularly useful for larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal.
Steps:
-
Divide the larger number by the smaller number and find the remainder.
-
Replace the larger number with the smaller number, and the smaller number with the remainder.
-
Repeat steps 1 and 2 until the remainder is 0. The last non-zero remainder is the GCF.
Let's apply this to find the GCF of 24 and 84:
-
84 ÷ 24 = 3 with a remainder of 12.
-
Now we consider 24 and 12. 24 ÷ 12 = 2 with a remainder of 0.
The last non-zero remainder is 12.
Therefore, the GCF of 24 and 84 is $\boxed{12}$.
Advantages of the Euclidean Algorithm:
- Efficient for large numbers: This method is significantly more efficient than prime factorization or listing factors for large numbers.
- Systematic and less prone to errors: The algorithm is straightforward and minimizes the chances of making mistakes.
Disadvantages of the Euclidean Algorithm:
- Less intuitive: The underlying mathematical principle might not be immediately obvious to beginners.
Applications of Finding the GCF
Finding the greatest common factor has practical applications in various areas, including:
-
Simplifying Fractions: The GCF is used to simplify fractions to their lowest terms. For example, the fraction 24/84 can be simplified to 2/7 by dividing both the numerator and denominator by their GCF (12).
-
Solving Word Problems: Many word problems involving dividing quantities into equal groups require finding the GCF to determine the largest possible group size.
-
Algebra and Number Theory: The GCF plays a crucial role in various algebraic manipulations and theorems in number theory.
-
Computer Science: Efficient algorithms for finding the GCF, like the Euclidean algorithm, are essential in computer science for various computational tasks.
-
Music Theory: The GCF helps in determining the common divisors of musical intervals, simplifying musical notation.
Conclusion
Finding the GCF of two numbers is a fundamental skill with broad applications. While simple methods like listing factors work well for small numbers, the prime factorization method offers a deeper understanding of the underlying concepts, and the Euclidean algorithm proves highly efficient for larger numbers. Choosing the appropriate method depends on the context and the size of the numbers involved. Mastering these techniques will not only enhance your mathematical skills but also provide you with valuable problem-solving capabilities applicable to diverse fields. Remember that understanding the why behind the calculations is just as important as knowing the how.
Latest Posts
Latest Posts
-
Probability Of Flipping 3 Heads In A Row
May 10, 2025
-
4 7 To The Power Of 2
May 10, 2025
-
How To Calculate Product Cost Per Unit
May 10, 2025
-
How Many Seconds In 17 Years
May 10, 2025
-
How Many Hours In Six Days
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 24 And 84 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.