What Is The Gcf Of 3 And 18
Treneri
May 10, 2025 · 5 min read
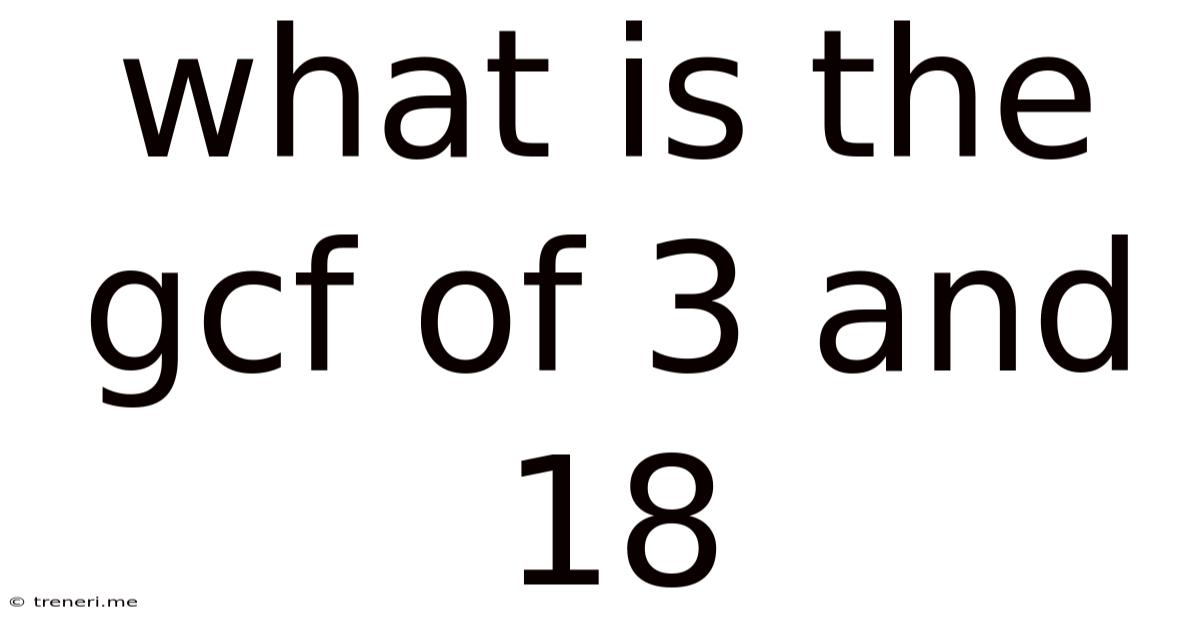
Table of Contents
What is the GCF of 3 and 18? A Deep Dive into Greatest Common Factors
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts opens doors to more complex mathematical ideas. This article will not only answer the question, "What is the GCF of 3 and 18?" but also explore the various methods for finding GCFs, delve into the significance of GCFs in mathematics and real-world applications, and touch upon related concepts like least common multiples (LCMs).
Understanding Greatest Common Factors (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest number that divides two or more integers without leaving a remainder. It's essentially the biggest number that's a factor of both numbers. Think of it as the largest shared building block of those numbers.
Example: Let's consider the numbers 12 and 18. The factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors are 1, 2, 3, and 6. The greatest of these common factors is 6. Therefore, the GCF of 12 and 18 is 6.
Finding the GCF of 3 and 18: Methods and Solutions
Now, let's address the specific question: What is the GCF of 3 and 18? We can use several methods to find this:
1. Listing Factors Method
This is the most straightforward method, especially for smaller numbers.
- Factors of 3: 1, 3
- Factors of 18: 1, 2, 3, 6, 9, 18
Comparing the lists, we see that the common factors are 1 and 3. The greatest of these is 3.
Therefore, the GCF of 3 and 18 is 3.
2. Prime Factorization Method
This method is more efficient for larger numbers. It involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
- Prime factorization of 3: 3 (3 is itself a prime number)
- Prime factorization of 18: 2 x 3 x 3 or 2 x 3²
To find the GCF, we identify the common prime factors and multiply them together. Both numbers share one factor of 3.
Therefore, the GCF of 3 and 18 is 3.
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF, especially for larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are the same.
Let's apply it to 3 and 18:
- 18 ÷ 3 = 6 with a remainder of 0.
- Since the remainder is 0, the GCF is the smaller number, which is 3.
Therefore, the GCF of 3 and 18 is 3.
Significance of GCFs in Mathematics and Real-World Applications
Understanding GCFs is crucial in various mathematical contexts and real-world scenarios:
-
Simplifying Fractions: GCFs are essential for simplifying fractions to their lowest terms. For example, the fraction 18/36 can be simplified by dividing both the numerator and denominator by their GCF, which is 18. This simplifies the fraction to 1/2.
-
Solving Equations: GCFs are used in various algebraic manipulations and equation solving. For instance, factoring expressions often involves finding the GCF of the terms.
-
Geometry Problems: GCFs are used in geometrical problems, particularly when dealing with shapes and their dimensions. Consider finding the largest square tile that can perfectly cover a rectangular floor of dimensions 12m x 18m. The answer is determined by the GCF of 12 and 18, which is 6m.
-
Real-World Applications: GCFs can be applied to many everyday tasks. For example, imagine you have 18 apples and 3 oranges. You want to distribute these fruits evenly among several bags, ensuring that each bag contains the same number of apples and the same number of oranges. The GCF will help you find the maximum number of bags possible (3 bags with 6 apples and 1 orange each).
Least Common Multiple (LCM) and its Relationship with GCF
The least common multiple (LCM) is another important concept closely related to the GCF. The LCM of two or more integers is the smallest positive integer that is divisible by all the numbers.
The relationship between GCF and LCM is defined by the following formula:
LCM(a, b) * GCF(a, b) = a * b
Where 'a' and 'b' are the two numbers.
Let's use this formula to find the LCM of 3 and 18:
We already know that GCF(3, 18) = 3.
LCM(3, 18) * 3 = 3 * 18
LCM(3, 18) = (3 * 18) / 3 = 18
Therefore, the LCM of 3 and 18 is 18. This makes sense because 18 is divisible by both 3 and itself.
Advanced Concepts and Further Exploration
For those interested in delving deeper, here are some advanced topics related to GCFs:
-
Euclidean Algorithm for More Than Two Numbers: The Euclidean algorithm can be extended to find the GCF of more than two numbers.
-
GCF and Modular Arithmetic: GCFs play a significant role in modular arithmetic, a branch of number theory dealing with remainders in division.
-
Applications in Cryptography: GCFs and related concepts are fundamentally important in various cryptographic algorithms.
Conclusion
Finding the GCF of 3 and 18, which is 3, is a straightforward process. However, understanding the underlying principles and methods—listing factors, prime factorization, and the Euclidean algorithm—provides a solid foundation for tackling more complex problems involving GCFs and LCMs. The ability to determine GCFs is vital not only in abstract mathematics but also in various real-world scenarios, highlighting its practical importance. This article aims to provide a comprehensive understanding of the concept, encouraging further exploration and application of this fundamental mathematical tool.
Latest Posts
Latest Posts
-
What Is A Good Tanning Uv
May 10, 2025
-
Cuanto Es 8 Onzas En Litros
May 10, 2025
-
Round 66 To The Nearest Ten
May 10, 2025
-
Cuanto Falta Para El 18 De Noviembre
May 10, 2025
-
If A Triangle Has A Height Of 12 Inches
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 3 And 18 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.