What Is The Gcf Of 34 And 51
Treneri
May 11, 2025 · 5 min read
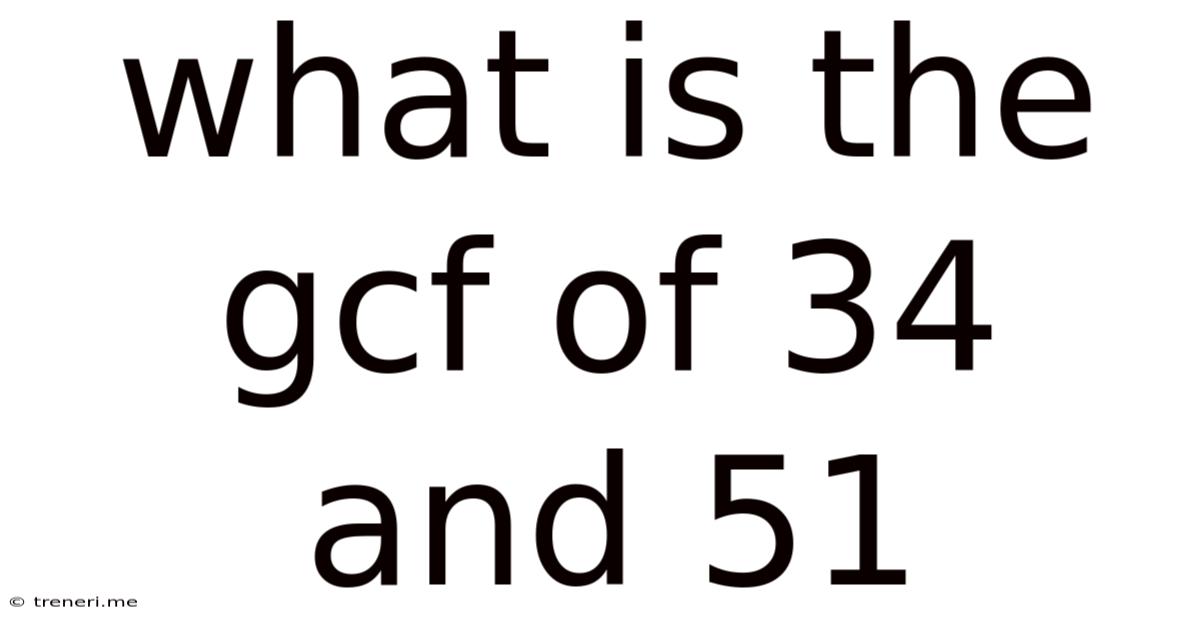
Table of Contents
What is the GCF of 34 and 51? A Deep Dive into Greatest Common Factor
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts and different methods can significantly improve your mathematical skills and problem-solving abilities. This article will explore the GCF of 34 and 51 in detail, offering multiple approaches to solve this problem and providing a broader understanding of GCFs and their applications.
Understanding the Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers evenly. Understanding GCFs is crucial in various mathematical operations, including simplifying fractions, solving algebraic equations, and working with geometric problems.
Method 1: Listing Factors
The most straightforward method to find the GCF is by listing all the factors of each number and identifying the largest common factor.
Factors of 34: 1, 2, 17, 34 Factors of 51: 1, 3, 17, 51
By comparing the lists, we can see that the common factors are 1 and 17. Therefore, the GCF of 34 and 51 is 17.
This method is suitable for smaller numbers, but it becomes less efficient as the numbers get larger. For larger numbers, more sophisticated methods are necessary.
Method 2: Prime Factorization
Prime factorization involves breaking down a number into its prime factors—numbers divisible only by 1 and themselves. This method is particularly helpful for larger numbers.
Prime factorization of 34: 2 x 17 Prime factorization of 51: 3 x 17
Both 34 and 51 share the prime factor 17. Therefore, the GCF of 34 and 51 is 17.
This method offers a systematic approach, even for larger numbers. It's considered one of the most reliable methods for finding the GCF.
Method 3: Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the GCF of two numbers, especially when dealing with larger numbers. This iterative algorithm is based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process continues until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 34 and 51:
- 51 - 34 = 17
- Now we find the GCF of 34 and 17.
- 34 - 17 = 17
- Since both numbers are now 17, the GCF of 34 and 51 is 17.
The Euclidean algorithm is remarkably efficient and avoids the need to list all factors, making it a preferred method for larger numbers. It's a cornerstone of number theory and has numerous applications beyond finding GCFs.
Applications of GCF
Understanding and applying the GCF has several practical applications across various mathematical fields and real-world scenarios:
1. Simplifying Fractions:
The GCF is essential for simplifying fractions to their lowest terms. To simplify a fraction, divide both the numerator and the denominator by their GCF. For example, if you have the fraction 34/51, dividing both by their GCF (17) simplifies the fraction to 2/3.
2. Solving Word Problems:
Many word problems involving division and sharing require finding the GCF. For example, if you have 34 apples and 51 oranges, and you want to divide them into identical bags with the same number of apples and oranges in each bag, the GCF (17) determines the maximum number of bags you can create. Each bag will contain 2 apples and 3 oranges.
3. Geometry and Measurement:
GCF is applied in geometric problems involving area and perimeter calculations. For example, if you need to tile a rectangular floor with square tiles of identical size, the side length of the square tiles will be a common factor of the floor's dimensions. The largest possible tile size will be the GCF of the floor's dimensions.
4. Algebra and Number Theory:
GCF plays a crucial role in algebraic manipulations and number theory. It is used in simplifying expressions, solving Diophantine equations, and proving various mathematical theorems.
Beyond the Basics: Exploring Further Concepts
While finding the GCF of 34 and 51 provides a solid foundation, delving deeper into related concepts enhances mathematical understanding.
Least Common Multiple (LCM):
The least common multiple (LCM) is the smallest positive integer that is a multiple of two or more numbers. The relationship between GCF and LCM is expressed by the formula:
LCM(a, b) x GCF(a, b) = a x b
Knowing the GCF of two numbers allows you to easily calculate their LCM. In the case of 34 and 51, since their GCF is 17, their LCM is (34 x 51) / 17 = 102.
Relatively Prime Numbers:
Two numbers are considered relatively prime or coprime if their GCF is 1. For example, the numbers 15 and 28 are relatively prime because their GCF is 1.
GCF of More Than Two Numbers:
The concept of GCF extends to more than two numbers. To find the GCF of multiple numbers, you can use prime factorization or the Euclidean algorithm iteratively.
Practical Tips and Strategies
-
Start with the smaller number: When listing factors, begin with the factors of the smaller number. This reduces the amount of work needed.
-
Use prime factorization effectively: Organize your prime factorization neatly to avoid missing any factors.
-
Master the Euclidean algorithm: Practice the Euclidean algorithm to become comfortable with its efficient process, especially for larger numbers.
-
Apply GCF in different contexts: Solve various problems involving GCF to build a deeper understanding and improve your problem-solving skills.
-
Use online calculators (for verification): Numerous online GCF calculators are available to verify your results. However, it's crucial to understand the underlying methods to build your mathematical skills. Do not rely solely on these calculators for learning.
Conclusion: Mastering the GCF
The GCF, while seemingly a simple concept, is a powerful tool with wide-ranging applications in mathematics and beyond. Understanding different methods for finding the GCF, like listing factors, prime factorization, and the Euclidean algorithm, empowers you to solve a variety of problems efficiently and accurately. By practicing these methods and exploring their applications, you can significantly enhance your mathematical abilities and problem-solving skills. The GCF of 34 and 51, being 17, serves as an excellent starting point for understanding this fundamental concept. Remember to practice and explore to fully grasp its significance and power.
Latest Posts
Latest Posts
-
Greatest Common Factor Of 30 And 36
May 12, 2025
-
Cups Of Flour In 10 Lb Bag
May 12, 2025
-
120 Days From May 20 2024
May 12, 2025
-
1 1 3 As An Improper Fraction
May 12, 2025
-
2420 Rounded To The Nearest Ten
May 12, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 34 And 51 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.