What Is The Gcf Of 36 And 27
Treneri
May 09, 2025 · 5 min read
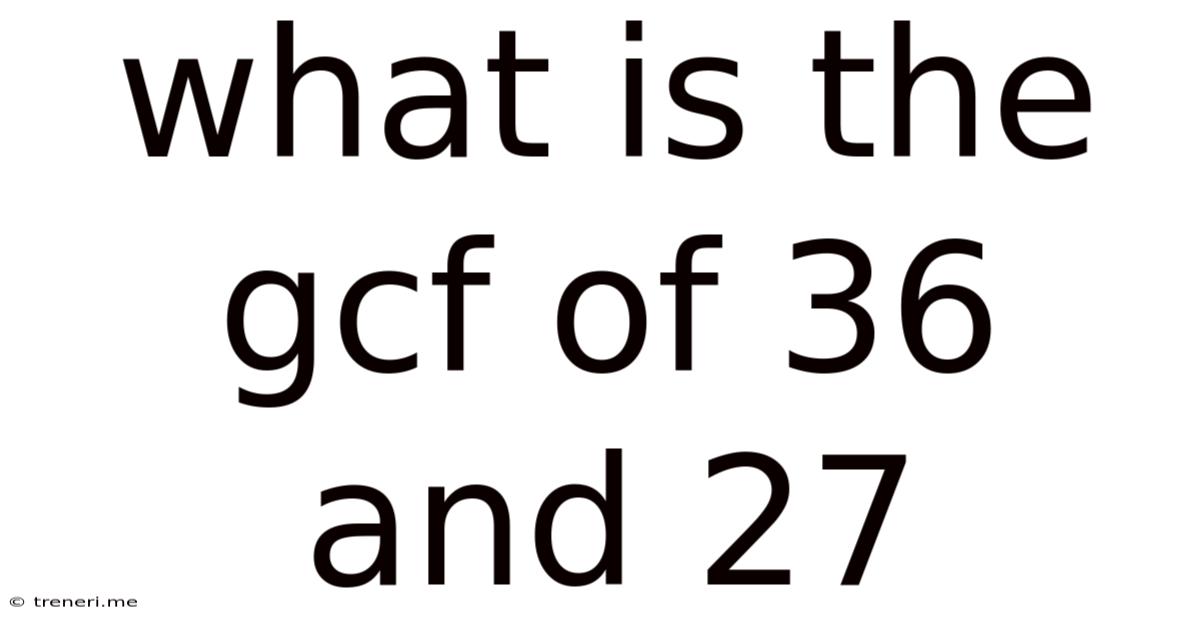
Table of Contents
What is the GCF of 36 and 27? A Deep Dive into Greatest Common Factors
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts and different methods for calculating it is crucial for various mathematical applications. This comprehensive guide will explore the GCF of 36 and 27, delve into various methods to determine it, and illuminate the significance of GCF in broader mathematical contexts.
Understanding Greatest Common Factors (GCF)
Before diving into the specifics of 36 and 27, let's solidify our understanding of GCF. The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that perfectly divides both numbers.
Think of it like finding the largest tile you can use to perfectly cover a rectangular area with dimensions matching your two numbers. The size of that tile represents the GCF.
Methods for Finding the GCF of 36 and 27
Several methods exist for calculating the GCF, each with its own advantages and disadvantages. Let's explore three common approaches:
1. Listing Factors Method
This method involves listing all the factors of each number and identifying the largest common factor.
- Factors of 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
- Factors of 27: 1, 3, 9, 27
By comparing the lists, we can see that the common factors are 1, 3, and 9. The greatest of these common factors is 9. Therefore, the GCF of 36 and 27 is 9. This method is straightforward for smaller numbers but becomes cumbersome for larger numbers with numerous factors.
2. Prime Factorization Method
This method utilizes the prime factorization of each number. Prime factorization is the process of expressing a number as a product of its prime factors (numbers divisible only by 1 and themselves).
- Prime factorization of 36: 2² x 3² (36 = 2 x 2 x 3 x 3)
- Prime factorization of 27: 3³ (27 = 3 x 3 x 3)
Once we have the prime factorizations, we identify the common prime factors and their lowest powers. Both 36 and 27 share the prime factor 3. The lowest power of 3 present in both factorizations is 3². Therefore, the GCF is 3² = 9. This method is efficient even for larger numbers, as it systematically breaks down the numbers into their prime components.
3. Euclidean Algorithm Method
The Euclidean algorithm is a highly efficient method for finding the GCF, particularly useful for larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 36 and 27:
- 36 - 27 = 9
- Now we find the GCF of 27 and 9.
- 27 - 9 = 18
- Now we find the GCF of 9 and 18.
- 18 - 9 = 9
- Now we find the GCF of 9 and 9. Since the numbers are equal, the GCF is 9.
The Euclidean algorithm provides a systematic and efficient way to find the GCF, even for very large numbers, avoiding the need to list factors or perform prime factorization, which can be time-consuming for larger values.
Significance of GCF in Mathematics and Real-World Applications
Understanding GCF isn't just an academic exercise; it has practical implications across various mathematical fields and real-world scenarios:
-
Simplifying Fractions: GCF is fundamental to simplifying fractions. To simplify a fraction, you divide both the numerator and the denominator by their GCF. For example, the fraction 36/27 can be simplified to 4/3 by dividing both by their GCF, 9.
-
Solving Algebraic Equations: GCF plays a vital role in factoring algebraic expressions. Factoring involves expressing an expression as a product of simpler expressions. Finding the GCF of the terms in an expression is often the first step in factoring.
-
Geometry and Measurement: GCF is useful in solving geometric problems involving area and volume. For example, if you need to tile a rectangular floor with square tiles of equal size, the side length of the largest possible square tile is the GCF of the floor's length and width.
-
Number Theory: GCF is a cornerstone concept in number theory, a branch of mathematics focused on the properties of integers. It's involved in various theorems and concepts, including modular arithmetic and Diophantine equations.
-
Computer Science: The Euclidean algorithm, used for calculating GCF, is a fundamental algorithm in computer science, employed in various cryptographic applications and data processing tasks.
Expanding on the Concept: Beyond 36 and 27
While we've focused on the GCF of 36 and 27, the principles and methods discussed apply to any pair of integers. Let's consider a slightly more complex example to reinforce the concepts:
Find the GCF of 144 and 108:
-
Listing Factors Method: This would become quite tedious for these larger numbers.
-
Prime Factorization Method:
- 144 = 2⁴ x 3²
- 108 = 2² x 3³
- The common prime factors are 2 and 3. The lowest powers are 2² and 3².
- Therefore, the GCF is 2² x 3² = 4 x 9 = 36
-
Euclidean Algorithm Method:
- 144 - 108 = 36
- 108 - 36 = 72
- 72 - 36 = 36
- 36 - 36 = 0
- The GCF is 36.
As you can see, even with larger numbers, the prime factorization and Euclidean algorithm methods remain efficient and effective. The listing factors method, however, quickly becomes impractical.
Conclusion: Mastering GCF for Mathematical Proficiency
The greatest common factor is a fundamental concept in mathematics with far-reaching applications. Understanding the various methods for calculating the GCF, particularly the prime factorization and Euclidean algorithm methods, equips you with the tools to tackle more complex mathematical problems efficiently. Whether you're simplifying fractions, factoring algebraic expressions, or solving geometric problems, a solid grasp of GCF is essential for mathematical proficiency. The seemingly simple question of "What is the GCF of 36 and 27?" opens the door to a deeper understanding of number theory and its practical relevance in various fields. Mastering this concept builds a strong foundation for further mathematical explorations and problem-solving.
Latest Posts
Latest Posts
-
74 Rounded To The Nearest Ten
May 09, 2025
-
What Angle Is A 6 12 Pitch
May 09, 2025
-
Calculating Cap Rate On Rental Property
May 09, 2025
-
4 914 Rounded To The Nearest Hundredth
May 09, 2025
-
Cuanto Es 50 Lb En Kilos
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 36 And 27 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.