What Is The Gcf Of 40 And 63
Treneri
May 10, 2025 · 5 min read
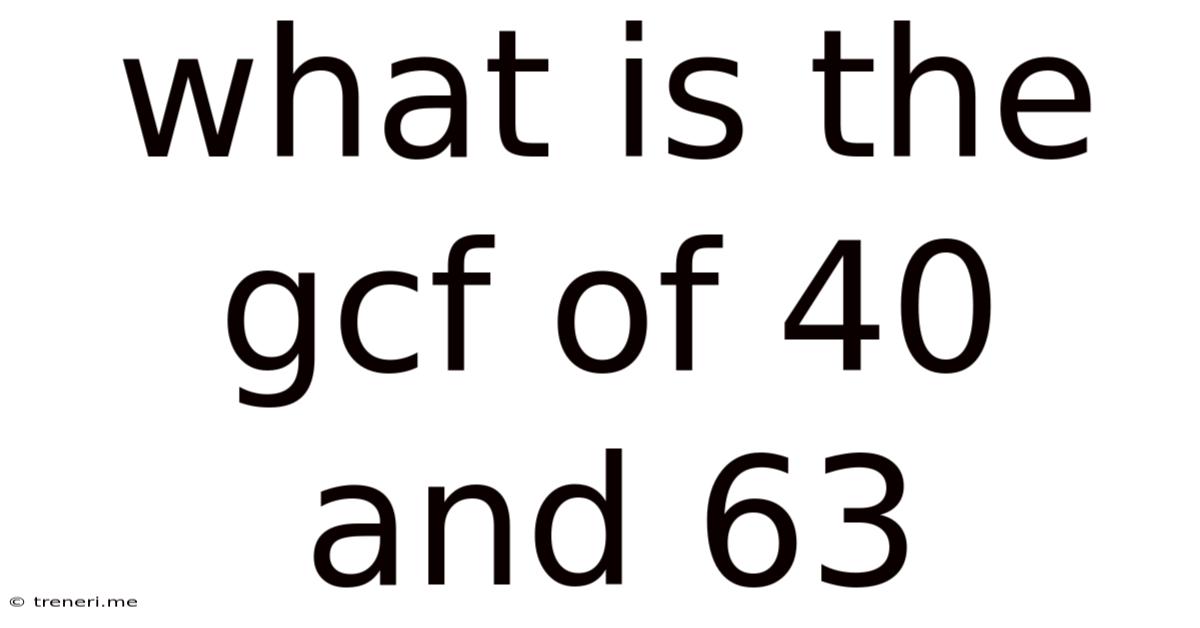
Table of Contents
What is the GCF of 40 and 63? A Deep Dive into Finding the Greatest Common Factor
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in mathematics with applications ranging from simplifying fractions to solving complex algebraic equations. This article will comprehensively explore how to determine the GCF of 40 and 63, and delve into various methods for finding the GCF of any two numbers. We'll also examine the practical significance of GCFs and their applications in diverse mathematical contexts.
Understanding the Greatest Common Factor (GCF)
The greatest common factor (GCF) of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that can be divided evenly into both numbers. For instance, the GCF of 12 and 18 is 6 because 6 is the largest number that divides both 12 and 18 without leaving a remainder.
Why is finding the GCF important?
Finding the GCF is crucial in various mathematical operations:
-
Simplifying fractions: The GCF allows us to reduce fractions to their simplest form. For example, the fraction 12/18 can be simplified to 2/3 by dividing both the numerator and denominator by their GCF, which is 6.
-
Solving algebraic equations: GCF is essential in factoring algebraic expressions, a process crucial for solving many equations.
-
Real-world applications: GCF finds applications in everyday scenarios, such as dividing objects into equal groups or determining the largest possible size of identical squares that can tile a rectangle.
Finding the GCF of 40 and 63: Different Methods
Let's now focus on determining the GCF of 40 and 63. We'll explore several methods:
1. Listing Factors Method
This method involves listing all the factors of each number and identifying the largest common factor.
- Factors of 40: 1, 2, 4, 5, 8, 10, 20, 40
- Factors of 63: 1, 3, 7, 9, 21, 63
Comparing the lists, we see that the only common factor is 1. Therefore, the GCF of 40 and 63 is 1.
2. Prime Factorization Method
This is a more systematic and efficient approach, especially for larger numbers. It involves finding the prime factorization of each number and then identifying the common prime factors raised to the lowest power.
- Prime factorization of 40: 2³ x 5
- Prime factorization of 63: 3² x 7
Comparing the prime factorizations, we see that there are no common prime factors. Therefore, the GCF of 40 and 63 is 1.
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers become equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 40 and 63:
- 63 = 1 x 40 + 23
- 40 = 1 x 23 + 17
- 23 = 1 x 17 + 6
- 17 = 2 x 6 + 5
- 6 = 1 x 5 + 1
- 5 = 5 x 1 + 0
The last non-zero remainder is 1, so the GCF of 40 and 63 is 1.
Relatively Prime Numbers
Numbers that have a GCF of 1 are called relatively prime or coprime. Since the GCF of 40 and 63 is 1, we can conclude that 40 and 63 are relatively prime numbers. This means they share no common factors other than 1.
Practical Applications of Finding the GCF
The concept of GCF extends beyond abstract mathematical exercises. It has practical applications in various fields:
-
Simplification of fractions: As mentioned earlier, reducing fractions to their lowest terms is crucial for clarity and ease of calculation. This involves dividing both the numerator and denominator by their GCF.
-
Measurement and Geometry: Imagine you have two pieces of wood, one measuring 40cm and the other 63cm. You want to cut them into smaller pieces of equal length, without any waste. The GCF will tell you the largest possible length of the pieces. In this case, the GCF of 40 and 63 is 1cm, meaning you can only cut each piece into 1cm long sections.
-
Scheduling and Planning: Imagine you have two events that repeat at different intervals. The GCF can help you determine when these events will coincide.
-
Computer Science: The GCF plays a vital role in cryptography and other areas of computer science.
-
Music Theory: The GCF is used to determine the simplest ratio of musical intervals.
Beyond Two Numbers: Finding the GCF of Multiple Numbers
The methods discussed above can be extended to find the GCF of more than two numbers. The prime factorization method remains particularly effective. For instance, to find the GCF of 40, 63, and 105:
-
Prime factorization:
- 40 = 2³ x 5
- 63 = 3² x 7
- 105 = 3 x 5 x 7
-
Identify common prime factors: The only common prime factor is 1.
-
GCF: The GCF of 40, 63, and 105 is 1.
Conclusion: The Importance of Understanding GCF
Understanding the greatest common factor is essential for a strong foundation in mathematics and its numerous applications. While the GCF of 40 and 63 might seem a simple calculation, the underlying principles and methods are fundamental to solving more complex mathematical problems. The ability to find the GCF efficiently, whether through listing factors, prime factorization, or the Euclidean algorithm, is a valuable skill in various fields, highlighting the importance of mastering this basic yet powerful mathematical concept. The fact that 40 and 63 are relatively prime numbers further emphasizes the significance of understanding their shared factors (or lack thereof). This knowledge provides valuable insights into number relationships and has practical implications across several disciplines.
Latest Posts
Latest Posts
-
Greatest Common Factor Of 4 And 18
May 10, 2025
-
How Many Cups Is A Quarter Pound Of Butter
May 10, 2025
-
Determine The Length Of Each Segment
May 10, 2025
-
How Many Stepping Stones Do I Need
May 10, 2025
-
Find The Area Of The Circle Pictured Above
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 40 And 63 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.