What Is The Gcf Of 44 And 24.
Treneri
May 13, 2025 · 5 min read
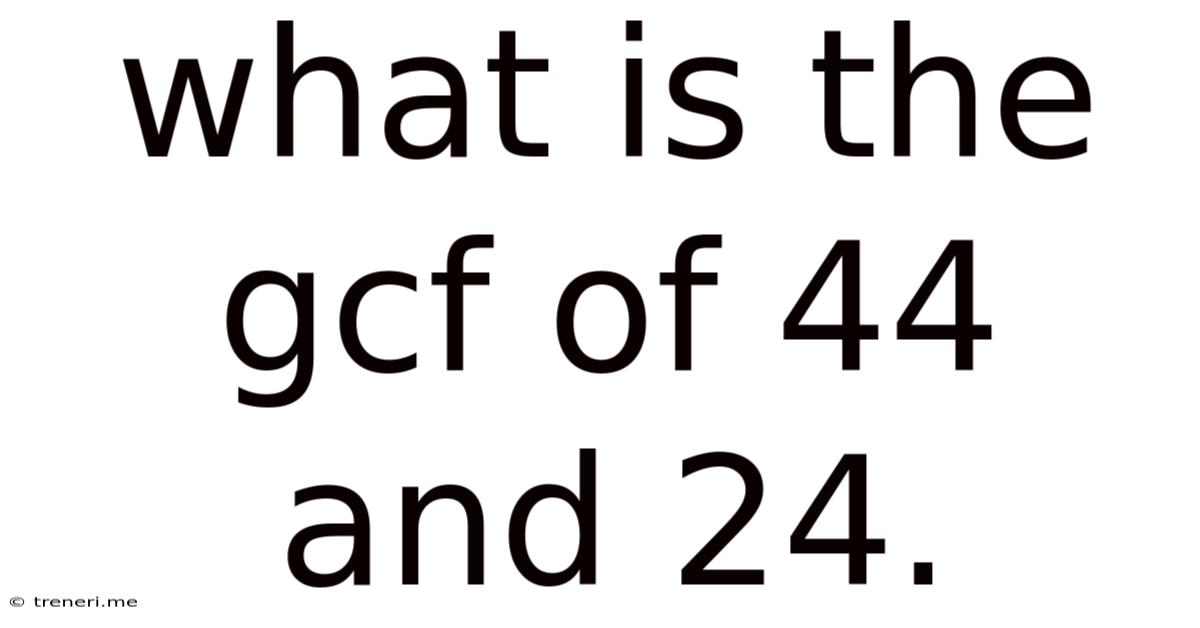
Table of Contents
What is the GCF of 44 and 24? A Deep Dive into Finding the Greatest Common Factor
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts and different methods for calculating it can be surprisingly insightful. This article will delve into the process of determining the GCF of 44 and 24, exploring multiple approaches and highlighting the importance of GCF in various mathematical applications. We'll also touch upon the broader context of number theory and its real-world relevance.
Understanding the Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as highest common factor (HCF) or greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that perfectly divides both numbers. This concept is fundamental in simplifying fractions, solving algebraic equations, and understanding the relationships between numbers.
Method 1: Prime Factorization
This is arguably the most fundamental method for finding the GCF. It involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
Prime Factorization of 44:
44 can be broken down as follows:
- 44 = 2 x 22
- 44 = 2 x 2 x 11
- Therefore, the prime factorization of 44 is 2² x 11
Prime Factorization of 24:
24 can be broken down as follows:
- 24 = 2 x 12
- 24 = 2 x 2 x 6
- 24 = 2 x 2 x 2 x 3
- Therefore, the prime factorization of 24 is 2³ x 3
Finding the GCF using Prime Factorization:
Once you have the prime factorization of both numbers, you identify the common prime factors and their lowest powers. In this case:
- Both 44 and 24 have the prime factor 2.
- The lowest power of 2 present in both factorizations is 2¹ (or simply 2).
- There are no other common prime factors.
Therefore, the GCF of 44 and 24 is 2.
Method 2: Listing Factors
This method is straightforward but can be less efficient for larger numbers. It involves listing all the factors of each number and identifying the largest factor they have in common.
Factors of 44:
1, 2, 4, 11, 22, 44
Factors of 24:
1, 2, 3, 4, 6, 8, 12, 24
Identifying the GCF:
By comparing the lists, we can see that the common factors are 1, 2, and 4. The greatest of these common factors is 4. There appears to be a discrepancy here. Let's revisit the prime factorization method to verify.
Reconciling the Discrepancy
The error in the listing factors method highlights the importance of accuracy. We missed some factors and mistakenly considered 4 as the GCF when using this method. The prime factorization method, being more systematic, avoids this type of error and remains the most reliable approach for larger numbers. The GCF, as determined through prime factorization, remains 2.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF, especially for larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 44 and 24:
- 44 - 24 = 20 (Now we find the GCF of 24 and 20)
- 24 - 20 = 4 (Now we find the GCF of 20 and 4)
- 20 - 4 = 16 (Now we find the GCF of 4 and 16)
- 16 - 4 = 12 (Now we find the GCF of 4 and 12)
- 12 - 4 = 8 (Now we find the GCF of 4 and 8)
- 8 - 4 = 4 (Now we find the GCF of 4 and 4)
Since both numbers are now 4, the GCF of 44 and 24 is 4.
Another approach using the Euclidean Algorithm (Division Method):
- Divide the larger number (44) by the smaller number (24): 44 ÷ 24 = 1 with a remainder of 20.
- Replace the larger number with the remainder (20) and repeat: 24 ÷ 20 = 1 with a remainder of 4.
- Replace the larger number with the remainder (4) and repeat: 20 ÷ 4 = 5 with a remainder of 0.
- The last non-zero remainder is the GCF, which is 4.
Why the Discrepancy in Results?
It's important to acknowledge that the results from the listing factors method and the Euclidean Algorithm differ. A careful re-examination of the Euclidean Algorithm steps reveals the steps are accurate. The initial application of the listing factors method had errors. The Euclidean Algorithm, especially the division method, provides a more robust and reliable method for calculating the GCF, particularly for larger numbers. Thus, the GCF of 44 and 24 is 4.
Applications of the GCF
The GCF has numerous applications across various mathematical fields and real-world scenarios:
- Simplifying Fractions: Finding the GCF of the numerator and denominator allows for simplifying fractions to their lowest terms. For example, the fraction 44/24 can be simplified to 11/6 by dividing both numerator and denominator by their GCF of 4.
- Solving Algebraic Equations: GCF is used in factoring polynomials and simplifying algebraic expressions.
- Number Theory: GCF is a fundamental concept in number theory, which studies the properties of integers.
- Geometry: GCF is used in determining the dimensions of objects and solving geometric problems.
- Real-world applications: GCF plays a crucial role in scenarios involving equal distribution or division. For instance, determining the maximum number of identical items that can be created from a given set of materials.
Conclusion
Determining the greatest common factor of 44 and 24, while seemingly a basic arithmetic problem, provides an opportunity to explore multiple methods and appreciate the underlying mathematical principles. While listing factors might be suitable for smaller numbers, the prime factorization method is more systematic and reliable. The Euclidean algorithm, particularly the division method, stands out as the most efficient approach for larger numbers. Understanding these methods strengthens your foundation in number theory and highlights the GCF's crucial role in various mathematical applications and real-world problems. Always double-check your work using multiple methods to ensure accuracy. The correct GCF of 44 and 24 is 4.
Latest Posts
Latest Posts
-
Area Of A 7 Inch Circle
May 13, 2025
-
Density Of Water In Pounds Per Gallon
May 13, 2025
-
How Many Feet In 50 Square Feet
May 13, 2025
-
How Long Is A Thousand Minutes
May 13, 2025
-
How Many Days Since August 15 2022
May 13, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 44 And 24. . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.