What Is The Gcf Of 5 And 20
Treneri
May 12, 2025 · 6 min read
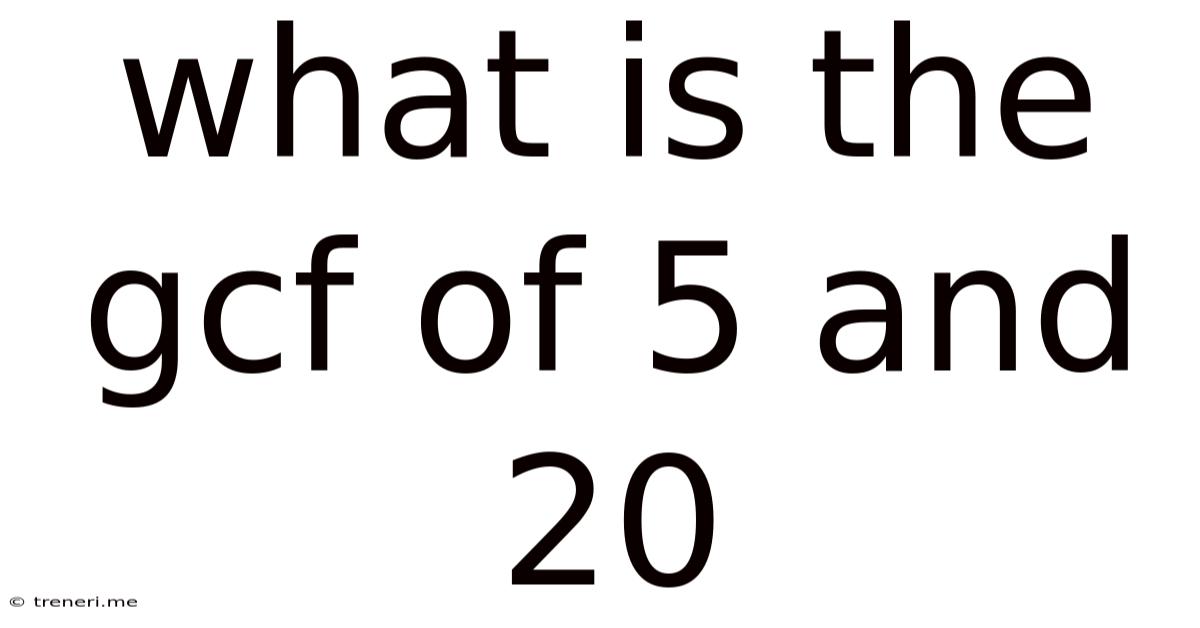
Table of Contents
What is the GCF of 5 and 20? A Deep Dive into Greatest Common Factors
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts and various methods involved opens doors to more advanced mathematical concepts. This article delves into the question, "What is the GCF of 5 and 20?", exploring not just the answer but also the broader significance of GCFs in mathematics and beyond.
Understanding Greatest Common Factors (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that fits perfectly into both numbers. For example, the GCF of 12 and 18 is 6 because 6 is the largest number that divides both 12 and 18 evenly.
Understanding GCFs is crucial for simplifying fractions, solving algebraic equations, and understanding various mathematical concepts. It forms a cornerstone of number theory and has applications in cryptography and computer science.
Methods for Finding the GCF
Several methods can efficiently determine the GCF of two or more numbers. Let's explore the most common approaches:
1. Listing Factors Method
This method involves listing all the factors of each number and then identifying the largest factor common to both.
Factors of 5: 1, 5 Factors of 20: 1, 2, 4, 5, 10, 20
The common factors of 5 and 20 are 1 and 5. The greatest common factor is therefore 5.
This method is straightforward for smaller numbers, but it becomes cumbersome and inefficient for larger numbers with numerous factors.
2. Prime Factorization Method
This method leverages the fundamental theorem of arithmetic, which states that every integer greater than 1 can be represented uniquely as a product of prime numbers (numbers divisible only by 1 and themselves).
Prime Factorization of 5: 5 (5 is a prime number) Prime Factorization of 20: 2 x 2 x 5 (20 = 2² x 5)
The common prime factor is 5. Therefore, the GCF of 5 and 20 is 5. This method is more efficient than the listing factors method, especially for larger numbers.
3. Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the GCF of two integers. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 5 and 20:
- 20 - 5 = 15. Now we find the GCF of 5 and 15.
- 15 - 5 = 10. Now we find the GCF of 5 and 10.
- 10 - 5 = 5. Now we find the GCF of 5 and 5.
- Since both numbers are now 5, the GCF is 5.
The Euclidean algorithm is particularly effective for larger numbers because it significantly reduces the number of calculations required compared to other methods.
The Significance of the GCF
The GCF holds significant importance in various mathematical contexts and real-world applications:
-
Simplifying Fractions: The GCF is essential for simplifying fractions to their lowest terms. Dividing both the numerator and denominator of a fraction by their GCF reduces the fraction without changing its value. For example, the fraction 20/100 can be simplified to 1/5 by dividing both the numerator and the denominator by their GCF, which is 20.
-
Solving Equations: GCFs play a crucial role in solving certain types of algebraic equations and Diophantine equations (equations where solutions are restricted to integers).
-
Number Theory: GCFs are fundamental in number theory, forming the basis for many theorems and proofs related to prime numbers, divisibility, and modular arithmetic.
-
Geometry: GCFs are used in geometric problems involving finding the dimensions of shapes that can be perfectly tiled or subdivided using smaller squares or other geometric figures. For example, if you have a rectangular garden with dimensions 20 meters by 5 meters, the GCF (5) tells you the largest square tile you can use to cover the entire garden without any gaps or overlaps.
-
Computer Science: The Euclidean algorithm, a primary method for finding the GCF, is frequently used in computer science algorithms for tasks such as cryptography and modular arithmetic. Its efficiency makes it crucial for applications requiring high-speed computations.
Beyond the Basics: Exploring Related Concepts
Understanding GCFs opens the door to related concepts:
-
Least Common Multiple (LCM): The least common multiple (LCM) is the smallest positive integer that is a multiple of each of the integers. The GCF and LCM are related by the formula: GCF(a, b) * LCM(a, b) = a * b. Therefore, if you know the GCF of two numbers, you can easily calculate their LCM.
-
Coprime Numbers: Two numbers are coprime (or relatively prime) if their GCF is 1. This means they share no common factors other than 1. For example, 5 and 12 are coprime.
-
Modular Arithmetic: GCFs are fundamental to modular arithmetic, a system of arithmetic where numbers "wrap around" upon reaching a certain value (the modulus). This is widely used in cryptography and computer science.
Practical Applications of GCFs
The concept of the greatest common factor extends beyond abstract mathematical exercises and finds practical application in various real-world scenarios. Here are some illustrative examples:
-
Sharing Items Equally: Imagine you have 20 apples and want to distribute them equally among 5 friends. The GCF (5) tells you that each friend will receive 5 apples. This concept is crucial in scenarios involving fair distribution of resources.
-
Construction and Measurement: In construction and engineering, finding the GCF can help determine optimal dimensions for materials or structures. For instance, knowing the GCF of dimensions could determine the largest square tile that can be used without any cuts or waste.
-
Music and Rhythm: The GCF plays a role in music theory when determining rhythmic patterns and common divisors of notes.
-
Data Compression: The GCF concept is utilized in some data compression algorithms to identify common factors and thus reduce data redundancy.
-
Project Management: In project planning, finding the GCF can assist in optimally scheduling tasks and resource allocation to minimize conflicts and maximize efficiency.
Conclusion: The Power of a Simple Concept
While the question "What is the GCF of 5 and 20?" may appear straightforward, exploring its answer reveals a world of mathematical depth and practical applications. From simplifying fractions to sophisticated algorithms in computer science, understanding GCFs is essential for navigating numerous mathematical and real-world problems. The methods discussed—listing factors, prime factorization, and the Euclidean algorithm—provide various approaches to finding the GCF, allowing you to choose the method best suited to the given numbers and context. By mastering the concept of GCFs, you unlock a deeper appreciation of the elegance and utility of mathematical principles. The simple act of finding the GCF of 5 and 20, therefore, serves as a gateway to a richer understanding of the interconnectedness of mathematical concepts and their relevance in our daily lives.
Latest Posts
Latest Posts
-
What Is The Equivalent Fraction Of 9 12
May 12, 2025
-
How Many Hours Are In Seven Days
May 12, 2025
-
Cuanto Es 18 Oz En Litros
May 12, 2025
-
How Many Miles Is 49 Km
May 12, 2025
-
Time And A Half For 22 An Hour
May 12, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 5 And 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.