What Is The Gcf Of 54 And 45
Treneri
May 13, 2025 · 6 min read
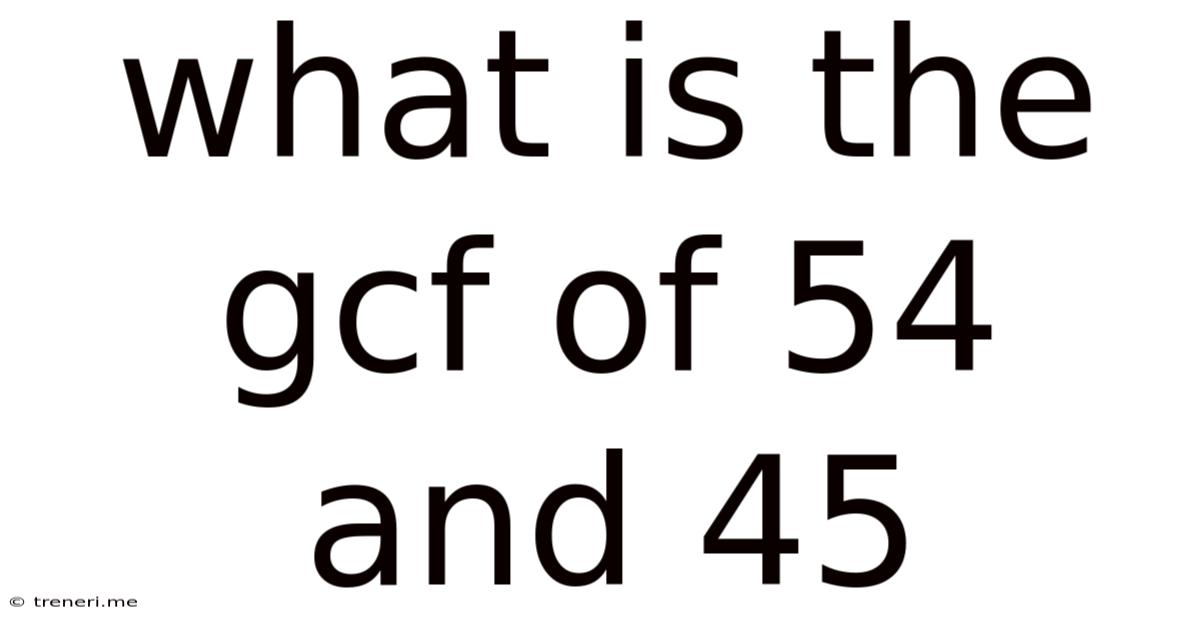
Table of Contents
What is the GCF of 54 and 45? A Comprehensive Guide to Finding the Greatest Common Factor
Finding the Greatest Common Factor (GCF), also known as the Greatest Common Divisor (GCD), is a fundamental concept in mathematics with applications ranging from simplifying fractions to solving algebraic equations. This article delves deep into the process of determining the GCF of 54 and 45, exploring various methods and providing a comprehensive understanding of the underlying principles. We'll move beyond a simple answer and equip you with the knowledge to tackle similar problems with confidence.
Understanding the Greatest Common Factor (GCF)
Before we dive into finding the GCF of 54 and 45, let's solidify our understanding of what the GCF represents. The GCF of two or more numbers is the largest number that divides evenly into all of them without leaving a remainder. Think of it as the biggest common divisor shared by the numbers. It's a crucial concept in simplifying fractions, factoring expressions, and solving various mathematical problems.
Why is finding the GCF important?
The GCF isn't just an abstract mathematical concept; it has practical applications in numerous fields:
-
Simplifying Fractions: Finding the GCF allows you to simplify fractions to their lowest terms. For instance, simplifying 18/27 requires finding the GCF of 18 and 27 (which is 9), reducing the fraction to 2/3.
-
Algebraic Simplification: In algebra, the GCF is used to factor expressions. Factoring allows us to simplify complex algebraic equations and solve them more efficiently.
-
Problem Solving: Many real-world problems, from dividing items equally to planning construction projects, involve finding the GCF to ensure optimal allocation and efficiency.
-
Number Theory: The GCF is a cornerstone of number theory, a branch of mathematics dedicated to the study of integers and their properties.
Methods for Finding the GCF of 54 and 45
There are several efficient methods for determining the GCF of two numbers, including:
1. Listing Factors Method
This method involves listing all the factors of each number and identifying the largest common factor.
Factors of 54: 1, 2, 3, 6, 9, 18, 27, 54 Factors of 45: 1, 3, 5, 9, 15, 45
By comparing the lists, we see that the common factors are 1, 3, and 9. The largest of these is 9. Therefore, the GCF of 54 and 45 is 9.
This method is straightforward for smaller numbers but can become cumbersome for larger numbers with many factors.
2. Prime Factorization Method
This method is more efficient for larger numbers. It involves finding the prime factorization of each number and then identifying the common prime factors raised to the lowest power.
Prime factorization of 54: 2 x 3 x 3 x 3 = 2 x 3³ Prime factorization of 45: 3 x 3 x 5 = 3² x 5
The common prime factor is 3. The lowest power of 3 in both factorizations is 3². Therefore, the GCF is 3² = 9.
This method is generally preferred for larger numbers as it is more systematic and less prone to errors.
3. Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the GCF of two numbers, particularly useful for larger numbers where listing factors or prime factorization becomes tedious. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 54 and 45:
- 54 - 45 = 9
- Now we find the GCF of 45 and 9.
- 45 - 9 = 36
- Now we find the GCF of 9 and 36.
- 36 - 9 = 27
- Now we find the GCF of 9 and 27.
- 27 - 9 = 18
- Now we find the GCF of 9 and 18.
- 18 - 9 = 9
- Now we find the GCF of 9 and 9. Since the numbers are equal, the GCF is 9.
A more efficient approach to the Euclidean Algorithm is to use repeated division with remainder.
- Divide the larger number (54) by the smaller number (45): 54 ÷ 45 = 1 with a remainder of 9.
- Replace the larger number with the smaller number (45) and the smaller number with the remainder (9).
- Repeat the division: 45 ÷ 9 = 5 with a remainder of 0.
- Since the remainder is 0, the GCF is the last non-zero remainder, which is 9.
This iterative process is significantly faster than the subtractive method, especially with larger numbers.
Applications of the GCF of 54 and 45
Now that we've established that the GCF of 54 and 45 is 9, let's look at how this knowledge can be applied:
-
Simplifying Fractions: If you had a fraction like 54/45, you could simplify it by dividing both the numerator and the denominator by their GCF (9), resulting in the simplified fraction 6/5.
-
Algebraic Factoring: Suppose you had an algebraic expression like 54x + 45y. You could factor out the GCF (9) to simplify the expression to 9(6x + 5y).
-
Real-World Scenarios: Imagine you have 54 red marbles and 45 blue marbles, and you want to divide them into identical bags with the maximum number of marbles in each bag. The GCF (9) tells you that you can create 9 bags, each containing 6 red marbles and 5 blue marbles.
Extending the Concept: GCF of More Than Two Numbers
The methods discussed above can be extended to find the GCF of more than two numbers. For instance, to find the GCF of 54, 45, and another number, say 27, you would first find the GCF of any two numbers (e.g., 54 and 45), which we know is 9. Then, you would find the GCF of that result (9) and the third number (27). The prime factorization method is particularly useful in these cases. The prime factorization of 27 is 3³. The common prime factor with the GCF of 54 and 45 (which is 3²) is 3, and the lowest power is 3². Therefore, the GCF of 54, 45, and 27 is 9.
Conclusion: Mastering GCF Calculations
Finding the Greatest Common Factor is a crucial skill in mathematics, with wide-ranging applications. This article provided a thorough exploration of how to find the GCF of 54 and 45 using multiple methods, illustrating the versatility and importance of this fundamental concept. By understanding these methods, you can confidently tackle similar problems, simplify fractions, factor algebraic expressions, and solve various real-world scenarios where finding the GCF is essential. Remember to choose the method that best suits the numbers involved for efficiency and accuracy. Whether it's listing factors, using prime factorization, or employing the Euclidean algorithm, mastering these techniques will greatly enhance your mathematical capabilities.
Latest Posts
Latest Posts
-
48 Square Meters To Square Feet
May 13, 2025
-
Least Common Factor Of 7 And 12
May 13, 2025
-
How Much Is 200 Grams In Lbs
May 13, 2025
-
Cuanto Es 2 Onzas En Cucharadas
May 13, 2025
-
Which Solid Has A Greater Volume 8 3 6 2
May 13, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 54 And 45 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.