What Is The Gcf Of 72 And 18
Treneri
May 09, 2025 · 5 min read
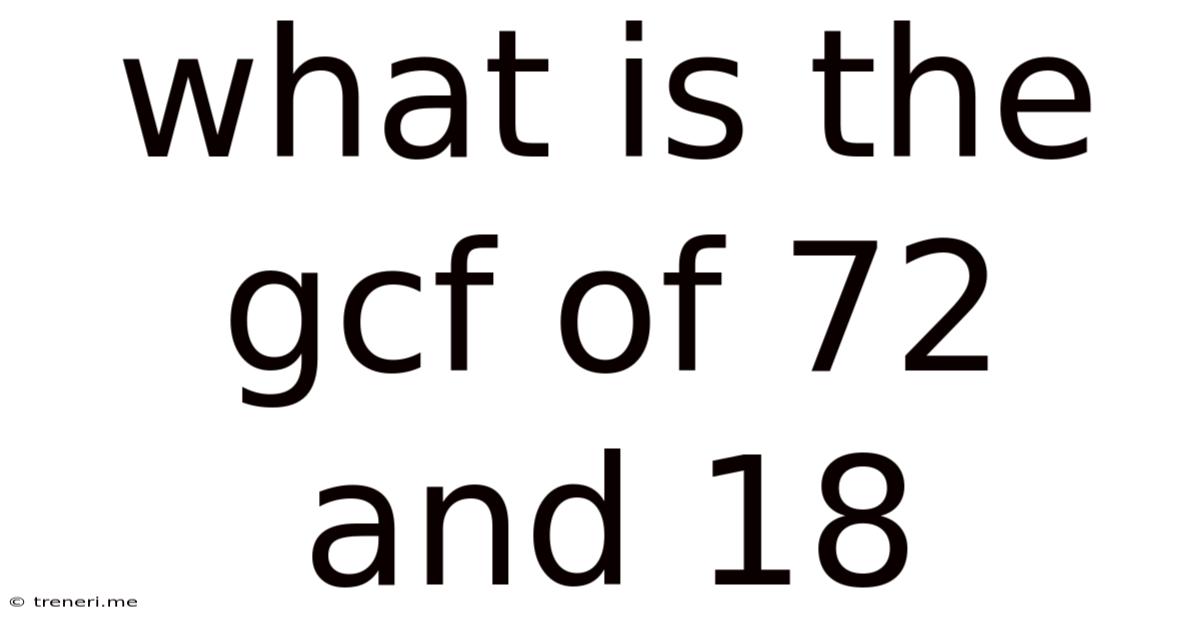
Table of Contents
What is the GCF of 72 and 18? A Deep Dive into Greatest Common Factors
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts and different methods for calculation opens doors to more advanced mathematical concepts. This article will delve into finding the GCF of 72 and 18, exploring multiple approaches and demonstrating their applications in broader mathematical contexts. We'll also explore the significance of GCF in various fields, solidifying its importance beyond basic arithmetic.
Understanding Greatest Common Factors (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers perfectly. For instance, if we consider the numbers 12 and 18, their common factors are 1, 2, 3, and 6. The greatest of these common factors is 6, therefore, the GCF of 12 and 18 is 6.
This concept is fundamental in simplifying fractions, solving algebraic equations, and understanding number theory. Mastering GCF calculation enhances your problem-solving skills and provides a solid foundation for more complex mathematical challenges.
Method 1: Listing Factors
The most straightforward method to find the GCF is by listing all the factors of each number and identifying the largest common one. Let's apply this to 72 and 18:
Factors of 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
Factors of 18: 1, 2, 3, 6, 9, 18
By comparing the two lists, we can see that the common factors are 1, 2, 3, 6, 9, and 18. The greatest of these common factors is 18. Therefore, the GCF of 72 and 18 is 18.
This method is efficient for smaller numbers but becomes cumbersome with larger numbers.
Method 2: Prime Factorization
Prime factorization is a more systematic and efficient method, particularly useful for larger numbers. It involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
Prime factorization of 72:
72 = 2 x 36 = 2 x 2 x 18 = 2 x 2 x 2 x 9 = 2 x 2 x 2 x 3 x 3 = 2³ x 3²
Prime factorization of 18:
18 = 2 x 9 = 2 x 3 x 3 = 2 x 3²
Once we have the prime factorization of both numbers, we identify the common prime factors and their lowest powers. Both 72 and 18 share a 2 and two 3s (3²).
Therefore, the GCF is 2¹ x 3² = 2 x 9 = 18.
This method is more efficient for larger numbers because it provides a structured approach to identifying common factors.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, especially large ones. It relies on repeated application of the division algorithm. The algorithm proceeds as follows:
- Divide the larger number by the smaller number and find the remainder.
- Replace the larger number with the smaller number and the smaller number with the remainder.
- Repeat steps 1 and 2 until the remainder is 0.
- The last non-zero remainder is the GCF.
Let's apply this to 72 and 18:
- 72 ÷ 18 = 4 with a remainder of 0.
Since the remainder is 0, the GCF is the last non-zero remainder, which is the smaller number, 18.
The Euclidean algorithm is particularly efficient for large numbers as it avoids the need to find all factors. Its efficiency makes it a preferred method in computational mathematics and computer science.
Applications of GCF
The concept of GCF extends far beyond simple arithmetic problems. It finds practical applications in various fields:
-
Simplifying Fractions: Finding the GCF is crucial for simplifying fractions to their lowest terms. For example, the fraction 72/18 can be simplified by dividing both the numerator and denominator by their GCF (18), resulting in the simplified fraction 4/1 or simply 4.
-
Algebra: GCF plays a significant role in factoring algebraic expressions. Finding the GCF of the terms in an expression allows you to factor it, simplifying equations and making them easier to solve.
-
Geometry: GCF helps in solving geometric problems involving areas and lengths. For example, finding the largest square tile that can perfectly cover a rectangular floor requires finding the GCF of the dimensions of the floor.
-
Number Theory: GCF is a fundamental concept in number theory, forming the basis for many advanced theorems and algorithms. It's essential for understanding concepts like modular arithmetic and cryptography.
-
Computer Science: The Euclidean algorithm, a method for finding the GCF, is widely used in computer science for tasks such as cryptographic key generation and simplifying calculations.
Beyond the Basics: Exploring LCM
Closely related to the GCF is the least common multiple (LCM). While the GCF is the largest number that divides both numbers, the LCM is the smallest number that is a multiple of both. Understanding the relationship between GCF and LCM is crucial for a deeper understanding of number theory.
The product of the GCF and LCM of two numbers is always equal to the product of the two numbers themselves. This relationship provides a convenient method for finding the LCM once the GCF is known.
For 72 and 18:
GCF (72, 18) = 18
Product of the numbers: 72 x 18 = 1296
LCM (72, 18) = 1296 / 18 = 72
This relationship simplifies the calculation of LCM, especially for larger numbers.
Conclusion: The Power of Understanding GCF
Finding the GCF of 72 and 18, as demonstrated through various methods, showcases the versatility and significance of this fundamental mathematical concept. Whether using the simple method of listing factors, the more efficient prime factorization, or the powerful Euclidean algorithm, the result remains consistent: the GCF of 72 and 18 is 18.
The importance of understanding GCF extends beyond simple arithmetic calculations. Its applications span various fields, from simplifying fractions and factoring algebraic expressions to more advanced concepts in number theory and computer science. By mastering the calculation and understanding the applications of GCF, you build a stronger foundation in mathematics and enhance your problem-solving abilities. The seemingly simple act of finding the greatest common factor unlocks a world of mathematical possibilities.
Latest Posts
Latest Posts
-
How To Find Height From Volume
May 11, 2025
-
How Many Teaspoons In 1 4 Oz Yeast
May 11, 2025
-
Cuanto Es 115 Minutos En Horas
May 11, 2025
-
How To Calculate The Heat Capacity Of A Calorimeter
May 11, 2025
-
How Many Hours Is 4000 Seconds
May 11, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 72 And 18 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.