What Is The Gcf Of 8 And 14
Treneri
May 09, 2025 · 5 min read
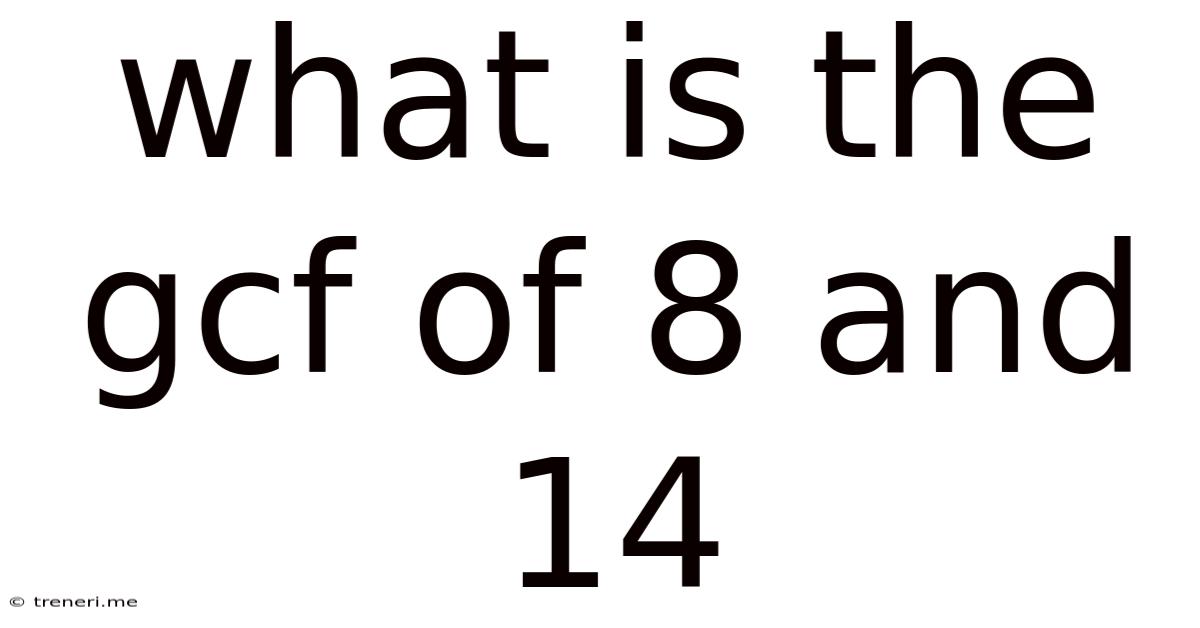
Table of Contents
What is the GCF of 8 and 14? A Deep Dive into Greatest Common Factors
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts and different methods for solving it offers valuable insights into number theory and its practical applications. This comprehensive guide will explore the GCF of 8 and 14, examining various approaches and highlighting the broader significance of GCFs in mathematics and beyond.
Understanding Greatest Common Factors (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that perfectly divides both numbers. Understanding GCFs is crucial in simplifying fractions, solving algebraic equations, and various other mathematical operations.
Why are GCFs Important?
GCFs have numerous applications across diverse fields:
-
Simplifying Fractions: Finding the GCF allows us to reduce fractions to their simplest form. For example, simplifying 12/18 requires finding the GCF of 12 and 18 (which is 6), resulting in the equivalent fraction 2/3.
-
Algebraic Simplification: GCFs play a vital role in factoring algebraic expressions, making them easier to solve and analyze.
-
Geometry and Measurement: GCFs are used in solving problems involving area, volume, and other geometric calculations. For instance, finding the largest square tile that can perfectly cover a rectangular floor requires determining the GCF of the floor's dimensions.
-
Cryptography: Number theory, which heavily relies on GCFs and related concepts like prime factorization, forms the foundation of many modern cryptographic systems.
Finding the GCF of 8 and 14: Methods and Solutions
Let's now delve into finding the GCF of 8 and 14 using several effective methods:
1. Listing Factors Method
This straightforward method involves listing all the factors of each number and then identifying the largest common factor.
- Factors of 8: 1, 2, 4, 8
- Factors of 14: 1, 2, 7, 14
Comparing the two lists, we see that the common factors are 1 and 2. The largest of these is 2. Therefore, the GCF of 8 and 14 is 2.
2. Prime Factorization Method
This method utilizes the prime factorization of each number to determine the GCF. Prime factorization involves expressing a number as a product of its prime factors.
- Prime factorization of 8: 2 x 2 x 2 = 2³
- Prime factorization of 14: 2 x 7
The common prime factor is 2. The lowest power of 2 present in both factorizations is 2¹. Therefore, the GCF is 2.
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF, especially for larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers become equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 8 and 14:
- 14 - 8 = 6 (Replace 14 with 6)
- 8 - 6 = 2 (Replace 8 with 2)
- 6 - 2 = 4 (Replace 6 with 4)
- 4 - 2 = 2 (Replace 4 with 2)
- Now we have 2 and 2.
Therefore, the GCF of 8 and 14 is 2.
Expanding on the Concept: Beyond 8 and 14
While we've focused on the GCF of 8 and 14, the principles discussed apply to any pair of integers. Let's explore some broader concepts:
GCF of More Than Two Numbers
The GCF can be extended to find the greatest common factor of more than two numbers. The methods described above, particularly prime factorization and the Euclidean algorithm (extended to handle multiple numbers), can be adapted for this purpose.
For example, to find the GCF of 12, 18, and 24:
- Prime factorization:
- 12 = 2² x 3
- 18 = 2 x 3²
- 24 = 2³ x 3
The common prime factors are 2 and 3. The lowest power of 2 is 2¹, and the lowest power of 3 is 3¹. Therefore, the GCF(12, 18, 24) = 2 x 3 = 6.
Least Common Multiple (LCM) and its Relationship to GCF
The least common multiple (LCM) is the smallest positive integer that is a multiple of each of the integers. The LCM and GCF are closely related:
For any two integers 'a' and 'b', the product of their GCF and LCM is equal to the product of the two numbers:
GCF(a, b) x LCM(a, b) = a x b
This relationship provides a convenient way to find the LCM if the GCF is known, and vice-versa. For 8 and 14:
GCF(8, 14) = 2
LCM(8, 14) = (8 x 14) / GCF(8, 14) = 112 / 2 = 56
Applications in Real-World Scenarios
Beyond mathematical exercises, GCFs find practical applications in various real-world scenarios:
-
Resource Allocation: Imagine dividing a group of 8 apples and 14 oranges into equal-sized bags, with each bag containing only one type of fruit. The GCF (2) indicates that you can create 2 bags, each with 4 apples and 7 oranges.
-
Project Management: If a project requires 8 hours of work from one team and 14 hours from another, the GCF helps determine the largest common block of time that can be used for scheduling meetings or progress updates.
-
Pattern Recognition: GCFs can be used to identify repeating patterns in data sets or sequences, useful in areas like signal processing and data analysis.
Conclusion: The Power of a Simple Concept
While initially appearing simple, the concept of the greatest common factor (GCF) underpins many significant mathematical principles and has wide-ranging applications in various fields. By understanding different methods for calculating the GCF, such as the listing factors, prime factorization, and Euclidean algorithm, we can effectively solve problems and gain valuable insights into numerical relationships. The GCF of 8 and 14, while a seemingly straightforward example, serves as a powerful illustration of these core concepts and their wider significance in mathematics and beyond. The exploration of GCFs extends beyond simple arithmetic, opening doors to a deeper understanding of number theory and its practical implications.
Latest Posts
Latest Posts
-
How To Find A Area Of A Rectangle
May 09, 2025
-
Calculate Top Speed From Gear Ratio
May 09, 2025
-
What Is The Gcf Of 40 And 32
May 09, 2025
-
How Do You Convert Mass To Volume
May 09, 2025
-
1 866 Rounded To The Nearest Hundredth
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 8 And 14 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.